Giải bài tập 5.36 trang 112 SGK Toán 9 tập 1 - Kết nối tri thức

Đề bài

Cho đường tròn (O) đường kính BC và điểm A (khác B và C).

a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O).

b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.

c) Với cùng giả thiết câu b), tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng BC = 6 cm.

Lời giải chi tiết

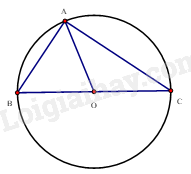
a) A nằm trên đường tròn tâm O nên AO = BO = CO

Tam giác ABC có AO là đường trung tuyến ứng với cạnh BC và \(AO = \frac{1}{2}BC\)

Nên tam giác ABC vuông tại A.

Chiều ngược lại:

Nếu tam giác ABC vuông tại A, gọi O là trung điểm của cạnh huyền BC thì ta có AO = BO = CO (tính chất đường trung tuyến trong tam giác vuông)

Từ đó ta có A, B, C thuộc đường tròn tâm O.

b)

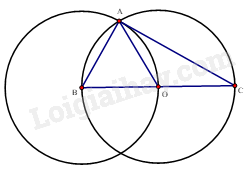
A là giao điểm của hai đường tròn (O) và (B) nên A thuộc (O) đường kính BC nên tam giác BAC vuông tại A.

Tam giác ABO có \(AB = BO = AO\) nên tam giác ABO đều suy ra \(\widehat {ABO} = \widehat {AOB} = \widehat {BAO} = {60^0}\)

Tam giác ABC vuông tại A nên \(\widehat B + \widehat C = {90^0}\) hay \({60^0} + \widehat C = {90^0}\) hay \(\widehat C = {30^0}\)

c) Ta có: \(\widehat {AOB} + \widehat {AOC} = {180^0}\) (hai góc kề bù)

nên \({60^0} + \widehat {AOC} = {180^0}\) hay \(\widehat {AOC} = {180^0} - {60^0} = {120^0}\)

Đường kính BC = 6 cm nên bán kỉnh đường tròn (O) là \(6:2 = 3\) cm

Độ dài cung AC là \(\frac{{2\pi .3.120}}{{360}} = 2\pi \) cm

Diện tích phần quạt chứa OA, OC là \(\frac{{\pi {R^2}.120}}{{360}} = \frac{{{3^2}\pi .120}}{{360}} = 3\pi \left( {c{m^2}} \right)\)