Giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo

Đề bài

 

Tìm tiệm cận của đồ thị hàm số khối lượng hạt \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\) trong Khởi động: Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)trong đó \({m_0}\) là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng.

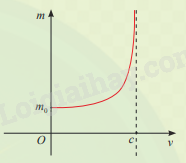
(Theo: https://www.britannica.com/science/relativistic-mass)

Lời giải chi tiết

Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)

Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \)

Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} =  + \infty \); \(\mathop {\lim }\limits_{v \to {c^ - }} m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} =  - \infty \)

Vậy đường thẳng x = c  là tiệm cận đứng của đồ thị hàm số