Giải bài tập 3 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạoTìm các tiệm cận của đồ thị hàm số sau: a) \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\) b) \(y = \frac{{{x^2} + x - 1}}{x}\) c) \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\) Tổng hợp đề thi giữa kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
Đề bài
Tìm các tiệm cận của đồ thị hàm số sau: a) \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\)
b) \(y = \frac{{{x^2} + x - 1}}{x}\)
c) \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\)
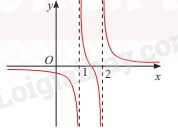
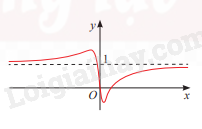
Phương pháp giải - Xem chi tiết Quan sát đồ thị Lời giải chi tiết a) Đường thẳng x = 1 và x = 2 là tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\) Đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\) b) Đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + x - 1}}{x}\) Đường thẳng y = \(x + 1\) là tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + x - 1}}{x}\) c) Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\)
|





















Danh sách bình luận