Giải bài tập 16 trang 67 SGK Toán 12 tập 2 - Chân trời sáng tạoĐề bài: Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như hình dưới đây. a) Tìm toạ độ các điểm (A), (B), (C), (D). b) Viết phương trình mặt phẳng (left( {ABC} right)) và mặt phẳng (left( {ACD} right)). c) Viết phương trình tham số của đường thẳng (AC). d) Cho biết đầu mũi tiện đang đặt tại điểm (Mleft( {0;60;40} right)). Tính khoảng cách từ điểm (M) đến mặt phẳng (left( {ABC} right)). Quảng cáo
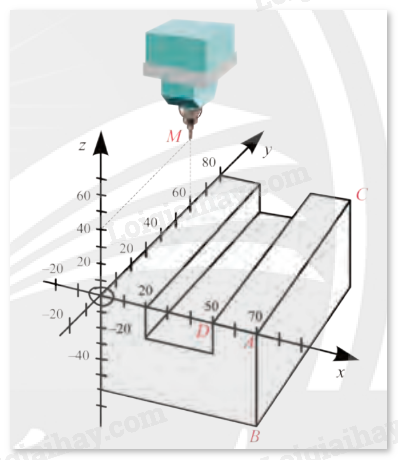
Đề bài Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như Hình 2. a) Tìm toạ độ các điểm \(A\), \(B\), \(C\), \(D\). b) Viết phương trình mặt phẳng \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ACD} \right)\). c) Viết phương trình tham số của đường thẳng \(AC\). d) Cho biết đầu mũi tiện đang đặt tại điểm \(M\left( {0;60;40} \right)\). Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {ABC} \right)\).
Phương pháp giải - Xem chi tiết a) Nhìn vào hình vẽ, xác định toạ độ các điểm \(A\), \(B\), \(C\), \(D\). b) Mặt phẳng \(\left( {ABC} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) nên một vectơ pháp tuyến của \(\left( {ABC} \right)\) là \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\), từ đó viết phương trình mặt phẳng \(\left( {ABC} \right)\). Mặt phẳng \(\left( {ACD} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \) nên một vectơ pháp tuyến của \(\left( {ACD} \right)\) là \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right]\), từ đó viết phương trình mặt phẳng \(\left( {ACD} \right)\). c) Đường thẳng \(AC\) có \(\overrightarrow {AC} \) là một vectơ chỉ phương, từ đó viết phương trình tham số của đường thẳng \(AC\). d) Sử dụng công thức tính khoảng cách để tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {ABC} \right)\). Lời giải chi tiết a) Dựa vào hình vẽ, ta có \(A\left( {70;0;0} \right)\), \(B\left( {70;0; - 60} \right)\), \(C\left( {70;80;0} \right)\) và \(D\left( {50;0;0} \right)\). b) Mặt phẳng \(\left( {ABC} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {AB} = \left( {0;0; - 60} \right)\) và \(\overrightarrow {AC} = \left( {0;80;0} \right)\) nên một vectơ pháp tuyến của \(\left( {ABC} \right)\) là \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {4800;0;0} \right)\). Ta suy ra \(\vec i = \left( {1;0;0} \right) = \frac{1}{{4800}}\overrightarrow {{n_1}} \) cũng là một vectơ pháp tuyến của \(\left( {ABC} \right)\). Vậy phương trình mặt phẳng \(\left( {ABC} \right)\) là \(1\left( {x - 70} \right) + 0\left( {y - 0} \right) + 0\left( {z - 0} \right) = 0\), hay \(x - 70 = 0\). Mặt phẳng \(\left( {ACD} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {AC} = \left( {0;80;0} \right)\) và \(\overrightarrow {AD} = \left( { - 20;0;0} \right)\) nên một vectơ pháp tuyến của \(\left( {ACD} \right)\) là \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right] = \left( {0;0;1600} \right)\). Ta suy ra \(\vec k = \left( {0;0;1} \right) = \frac{1}{{1600}}\overrightarrow {{n_2}} \) cũng là một vectơ pháp tuyến của \(\left( {ACD} \right)\). Vậy phương trình mặt phẳng \(\left( {ACD} \right)\) là \(0\left( {x - 70} \right) + 0\left( {y - 0} \right) + 1\left( {z - 0} \right) = 0\), hay \(z = 0\). c) Ta có \(\overrightarrow {AC} = \left( {0;80;0} \right)\) là một vectơ chỉ phương của đường thẳng \(AC\). Ta suy ra vectơ \(\vec j = \left( {0;1;0} \right) = \frac{1}{{80}}\overrightarrow {AC} \) cũng là một vectơ chỉ phương của \(AC\) Vậy phương trình tham số của \(AC\) là \(\left\{ \begin{array}{l}x = 70 + 0t\\y = 0 + t\\z = 0 + 0t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 70\\y = t\\z = 0\end{array} \right.\). d) Khoảng cách từ điểm \(M\) đến \(\left( {ABC} \right)\) là \(d\left( {M,\left( {ABC} \right)} \right) = \frac{{\left| {1.0 + 0.60 + 0.40 - 70} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} }} = 70.\)
|




















Danh sách bình luận