Bài 73 trang 147 SBT toán 7 tập 1

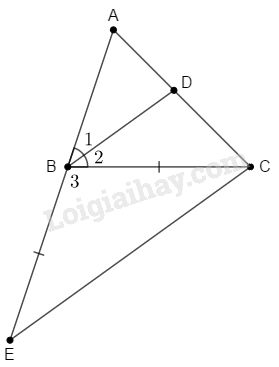
Đề bài

Cho tam giác \(ABC.\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Trên tia đối của tia \(BA\) lấy \(E\) sao cho \(BE = BC.\) Chứng minh rằng \(BD // EC.\)

Lời giải chi tiết

\( BD\) là tia phân giác của \(\widehat {ABC}\left( {gt} \right)\) 

Suy ra: \(\displaystyle \widehat {{B_1}} = \widehat {{B_2}} = {1 \over 2}\widehat {ABC}\) (1)

Lại có: \(BE =  BC\) (gt)

\( \Rightarrow  ∆BEC\) cân tại \(B\).

\( \Rightarrow \widehat E = \widehat {BCE}\) (tính chất tam giác cân)

\(∆BCE\) ta có \(\widehat {ABC}\) là góc ngoài tại đỉnh \(B\)

\( \Rightarrow \widehat {ABC} = \widehat E + \widehat {BCE}\) (tính chất góc ngoài của tam giác)

\( \Rightarrow \widehat {ABC} = 2\widehat E\).

\( \displaystyle \Rightarrow \widehat E = {1 \over 2}\widehat {ABC}\)

Kết hợp với (1) \( \displaystyle \Rightarrow \widehat E = \widehat {{B_1}} = {1 \over 2}\widehat {ABC}\)

Mà \(\widehat E,\;\widehat {{B_1}}\) ở vị trí đồng vị nên \(BD // CE.\)

Loigiaihay.com