Bài 7 trang 66 Vở bài tập toán 7 tập 2

Đề bài

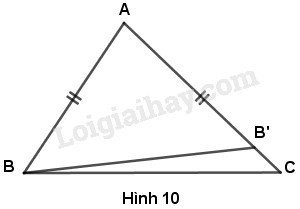
Một cách chứng minh khác của định lí 1 :

Cho tam giác \( {ABC}\) với \(AC > AB\). Trên tia \(AC\), lấy điểm \(B’\) sao cho \(AB’ = AB\) (h. 10).

a) Hãy so sánh góc \({ABC}\) với góc \({ABB'}\)

b) Hãy so sánh góc \({ABB'}\) với góc \({AB'B}\)

c) Hãy so sánh góc  \({AB'B}\) với góc \({ACB}\)

 Từ đó suy ra \(\widehat{ABC} > \widehat{ACB}\)

Lời giải chi tiết

a) Vì \(AB=AB'\) do đó \(AB' < AC\) nên \(B'\) nằm giữa hai điểm \(A\) và \(C\) do đó tia \(BB'\) nằm giữa hai tia \(BA\) và \(BC\), suy ra \(\widehat{ABC} > \widehat{ABB'}\).  (1) 

b) Xét tam giác \(ABB'\). Theo giả thiết ta có \(AB = AB'\) do đó tam giác \(ABB'\) cân tại \(A\) suy ra \( \widehat{ABB'} = \widehat{AB'B}\).  (2)

c) Ta có \(\widehat{AB'B}\) là góc ngoài tại đỉnh \(B'\) của tam giác \(BB'C\) nên \(\widehat {AB'B}>\widehat {ACB}\)                      (3)

Từ (1), (2) và (3) suy ra \(\widehat{ABC} > \widehat{ACB}\).

Loigiaihay.com