Bài 6 trang 200 SBT hình học 11Giải bài 6 trang 200 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30o. Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD). Quảng cáo
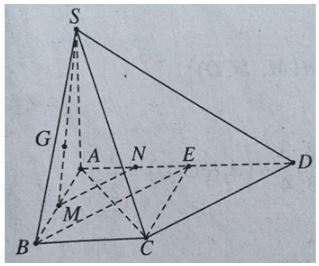
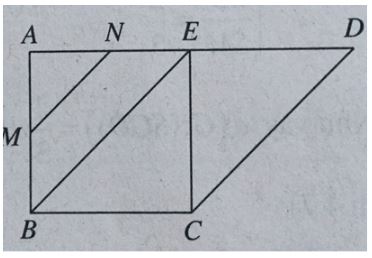
Đề bài Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30o. Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD). Lời giải chi tiết
+ Xác định góc của SC với (SAD). Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30o. ∠(CSE) cũng chính là góc giữa SC và mp(SAD). Trong ΔCSE, ta có: SE = CE.tan60o = a√3 ⇒ SA = √(SE2- AE2 ) = √(3a2 - a2 ) = a√2. Nhận xét Gọi M, N lần lượt là trung điểm của AB và AE. Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra d(M,(SCD)) = d(N,(SCD)). Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD)) + Xác định khoảng cách từ A đến (SCD). Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC. CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC). Hạ AH ⊥ SC, ta có AH ⊥ (SCD). Trong tam giác SAC, ta có:
Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
