Bài 6 trang 100 SBT toán 7 tập 1

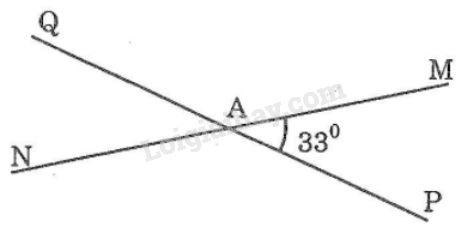
Đề bài

Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(A\) tạo thành góc \(MAP\) có số đo bằng \(33^\circ \).

a) Tính số đo góc \(NAQ.\)

b) Tính số đo góc \(MAQ.\)

c) Viết tên các cặp góc đối đỉnh.

d) Viết tên các cặp góc bù nhau.

Lời giải chi tiết

a) Ta có:

\(\widehat {NAQ}\) và \(\widehat {PAM}\) là hai góc đối đỉnh

Suy ra: \(\widehat {NAQ} = \widehat {PAM}\)

Mà \(\widehat {PAM} = 33^\circ \) nên \(\widehat {NAQ} = 33^\circ \)

b) \(\widehat {PAM}\) và \(\widehat {MAQ}\) là hai góc kề bù nên \(\widehat {PAM} + \widehat {MAQ} = 180^\circ \)

Suy ra: \(\widehat {MAQ} = 180^\circ  - \widehat {PAM} = 180^\circ  - 33^\circ\)\(\,  = 147^\circ \)

c) Các cặp góc đối đỉnh là \(\widehat {PAM}\) và \(\widehat {NAQ}\); \(\widehat {PAN}\) và \(\widehat {MAQ}\)

d) Các cặp góc bù nhau là:

\(\widehat {PAM}\) và \(\widehat {MAQ}\); \(\widehat {PAM}\) và \(\widehat {PAN}\); 

\(\widehat {NAQ}\) và \(\widehat {PAN}\); \(\widehat {NAQ}\) và \(\widehat {QAM}\).

Loigiaihay.com