Bài 58 trang 18 SBT toán 7 tập 1

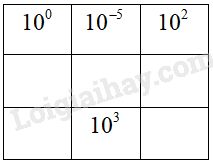
Đề bài

Hình vuông dưới đây có tính chất: mỗi ô ghi một lũy thừa của \(10\); tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.  Hãy điền các số còn thiếu vào các ô trống:

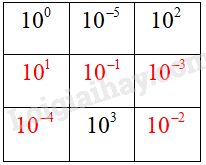
Lời giải chi tiết

Xét tích các số ở hàng thứ nhất ta được: \({10^0}{.10^{ - 5}}{.10^2} = {10^{0 + \left( { - 5} \right) + 2}} = {10^{ - 3}}\)

Ta có tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau (bằng \({10^{ - 3}}\)).

Xét cột thứ hai, ô trống thứ hai cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^{ - 5}}{{.10}^3}} \right) = {10^{ - 3}}:{10^{ - 2}} \)\(\,= {10^{\left( { - 3} \right) - \left( { - 2} \right)}} = {10^{ - 1}}\)

Xét đường chéo thứ nhất, ô trống cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^0}{{.10}^{ - 1}}} \right) = {10^{ - 3}}:{10^{ - 1}} \)\(\,= {10^{\left( { - 3} \right) - \left( { - 1} \right)}} = {10^{ - 2}}\)

Xét cột thứ ba, ô trống thứ ba cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^2}{{.10}^{ - 2}}} \right) = {10^{ - 3}}:{10^0} = {10^{ - 3}}\)

Xét hàng thứ hai, ô trống thứ nhất cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^{ - 3}}{{.10}^{ - 1}}} \right) = {10^{ - 3}}:{10^{ - 4}} \)\(\,= {10^{\left( { - 3} \right) - \left( { - 4} \right)}} = {10^1}\)

Xét hàng thứ ba, ô trống thứ nhất cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^3}{{.10}^{ - 2}}} \right) = {10^{ - 3}}:{10^1} \)\(\,= {10^{\left( { - 3} \right) - 1}} = {10^{ - 4}}\)

Ta được bảng sau:

Loigiaihay.com