Bài 55 trang 47 SBT toán 7 tập 2Giải bài 55 trang 47 sách bài tập toán 7. Cho hai điểm D, E nằm trên đường trung trực của đoạn thẳng BC. Chứng minh rằng ∆BDE = ∆CDE. Quảng cáo
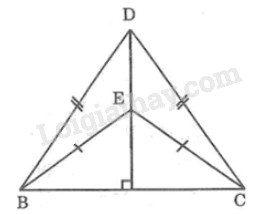
Đề bài Cho hai điểm \(D, E \) nằm trên đường trung trực của đoạn thẳng \(BC.\) Chứng minh rằng \(∆BDE = ∆CDE.\) Phương pháp giải - Xem chi tiết Sử dụng: +) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó +) Trường hợp bằng nhau thứ nhất: cạnh - cạnh - cạnh Lời giải chi tiết
Vì \(D\) thuộc đường trung trực của \(BC\) \( \Rightarrow DB = DC\) (tính chất đường trung trực) Vì \(E\) thuộc đường trung trực của \(BC\) \( \Rightarrow EB = EC\) (tính chất đường trung trực) Xét \(∆BDE\) và \(∆CDE\) có: +) \(DB = DC\) (chứng minh trên) +) \(DE\) cạnh chung +) \(EB = EC\) (chứng minh trên) Do đó: \(∆BDE = ∆CDE\) (c.c.c) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
