Bài 57 trang 47 SBT toán 7 tập 2

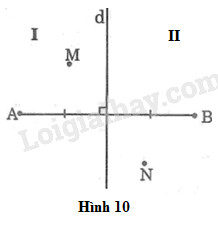
Đề bài

Đường trung trực \(d\) của đoạn thẳng \(AB\) chia mặt phẳng thành hai phần \(I\) và \(II\) như trên hình 10. Cho điểm \(M\) thuộc phần \(I\) và điểm \(N\) thuộc phần \(II.\) Chứng minh rằng:

a) \(MA < MB\)

b) \(NA > NB\) 

Lời giải chi tiết

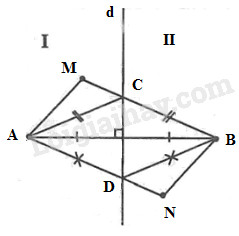
a) Nối \(MA, MB.\) Gọi \(C\) là giao điểm của MB với đường thẳng \(d,\) nối \(CA.\) 

Ta có:  \(MB = MC + CB\)

Mà \(CA = CB\) (tính chất đường trung trực)

Suy ra: \( MB = MC + CA\) (1)

Trong \(∆ MAC\) ta có:

\(MA < MC + CA\) (bất đẳng thức tam giác)  (2)

Từ (1) và (2) suy ra:  \(MA < MB\)

b) Nối \(NA, NB.\) Gọi \(D\) là giao điểm của \(NA\) với đường thẳng \(d,\) nối \(DB.\)

Ta có: \(NA = ND  + DA\)

Mà: \(DA = DB\) (tính chất đường trung trực)

Suy ra:  \(NA =  ND + DB \)   (3)

Trong \(∆NDB\) ta có:

\(NB < ND  + DB\) (bất đẳng thức tam giác)  (4)

Từ (3) và (4) suy ra:  \(NA > NB\) 

Loigiaihay.com