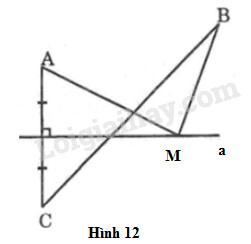
Bài 62 trang 48 SBT toán 7 tập 2Giải bài 62 trang 48 sách bài tập toán 7. Cho hình 12, M là một điểm tùy ý nằm trên đường thẳng a. Vẽ điểm C sao cho a là đường trung trực của AC. a) Hãy so sánh MA + MB với BC... Quảng cáo
Đề bài Cho hình 12, \(M\) là một điểm tùy ý nằm trên đường thẳng \(a.\) Vẽ điểm \(C\) sao cho \(a\) là đường trung trực của \(AC.\) a) Hãy so sánh \(MA + MB\) với \(BC.\) b) Tìm vị trí của điểm \(M\) trên đường thẳng \(a\) để \(MA + MB\) là nhỏ nhất.
Phương pháp giải - Xem chi tiết Sử dụng: +) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó +) Trong một tam giác, tổng hai cạnh luôn lớn hơn cạnh còn lại Lời giải chi tiết
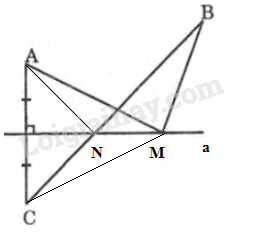
a) Gọi \(N\) là giao điểm của \(BC\) với đường thẳng \(a.\) +) Nếu \(M \ne N\) Nối \(MC\) Vì \(a\) là đường trung trực của \(AC\) mà \(M ∈ a\) \( \Rightarrow MA = MC\) (tính chất đường trung trực) (1) Trong \(∆MBC\) ta có: \(BC < MB + MC\) (bất đẳng thức tam giác) (2) Thay (1) vào (2) ta có: \(BC < MA + MB\) +) Nếu \(M\) trùng với \(N,\) ta nối \(NA\) Vì \(a\) là đường trung trực của \(AC\) mà \(N ∈ a\) \( \Rightarrow NA = NC\) (tính chất đường trung trực) Nên \(MA + MB = NA + NB\)\( = NC + NB = BC\) Vậy: \(MA + MB ≥ BC\) b) Theo chứng minh câu a ta có: Khi \(M\) trùng với \(N\) thì \(MA + MB = BC\) là nhỏ nhất. Vậy \(M\) là giao điểm của \(BC\) với đường thẳng \(a\) thì \(MA + MB\) nhỏ nhất. Loigiaihay.com
|





















Danh sách bình luận