Bài 7.1, 7.2, 7.3 phần bài tập bổ sung trang 48, 49 SBT toán 7 tập 2Giải bài 7.1, 7.2, 7.3 phần bài tập bổ sung trang 48, 49 sách bài tập toán 7. Trên đường trung trực của đoạn thẳng AB, lấy hai điểm phân biệt M, N. Khi đó khẳng định nào sau đây đúng?... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Bài 7.1 Trên đường trung trực của đoạn thẳng \(AB,\) lấy hai điểm phân biệt \(M, N.\) Khi đó khẳng định nào sau đây đúng? \(\left( A \right)\widehat {AMN} \ne \widehat {BMN}\) \(\left( B \right)\widehat {MAN} \ne \widehat {MBN}\) \(\left( C \right)\widehat {MNA} \ne \widehat {MNB}\) \(\left( D \right)\Delta AMN = \Delta BMN\) Phương pháp giải: Sử dụng: +) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó +) Tính chất hai tam giác bằng nhau Lời giải chi tiết:
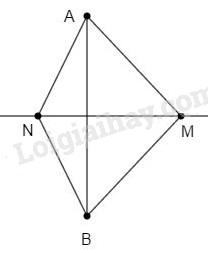
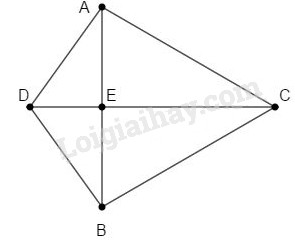
Vì \(M\) thuộc đường trung trực của đoạn thẳng \(AB\) nên \(MA = MB.\) Vì \(N\) thuộc đường trung trực của đoạn thẳng \(AB\) nên \(NA = NB.\) +) Xét \(∆AMN\) và \(∆BMN\) có: \(MA = MB\) ( chứng minh trên) \(NA = NB\) (chứng minh trên) Cạnh \(MN\) chung Suy ra \(∆AMN = ∆BMN\) (c.c.c) Do đó: \(\widehat {AMN} = \widehat {BMN}\) \(\widehat {MAN} = \widehat {MBN}\) \(\widehat {MNA}= \widehat {MNB}\) Hay các khẳng định (A), (B), (C) sai, (D) đúng. Chọn D. Bài 7.2 Cho hai tam giác cân chung đáy \(ABC\) và \(ABD,\) trong đó \(ABC\) là tam giác đều. Gọi \(E\) là trung điểm của \(AB.\) Khi đó, khẳng định nào sau đây là sai? (A) Đường thẳng \(CD\) là đường trung trực của \(AB.\) (B) Điểm \(E\) không nằm trên đường thẳng \(CD.\) (C) Đường trung trực của \(AC\) đi qua \(B.\) (D) Đường trung trực của \(BC\) đi qua \(A.\) Phương pháp giải: Sử dụng: +) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó +) Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó Lời giải chi tiết:
Vì tam giác \(ABD\) cân tại D nên \(DA=DB\) (định nghĩa tam giác cân). Suy ra: D nằm trên đường trung trực của AB. (1) Vì tam giác \(ABC\) đều nên \(CA=CB\) Suy ra: C nằm trên đường trung trực của AB (2) Từ (1) và (2) suy ra: \(DC\) là đường trung trực của \(AB\) Suy ra \(DC\bot AB\) tại trung điểm của \(AB\). Mà \(E\) là trung điểm của AB nên \(E \in CD\), suy ra B sai. Tam giác \(ABC\) đều nên \(BA=BC=AC\) hay \(B\) thuộc đường trung trực của \(AC\) và \(A\) thuộc đường trung trực của \(BC\). Chọn B. Bài 7.3 Đường trung trực của cạnh \(BC\) trong tam giác \(ABC\) cắt cạnh \(AC\) tại \(D.\) Hãy tìm: a) \(AD\) và \(CD\) nếu \(BD = 5cm; AC = 8cm;\) b) \(AC\) nếu \(BD = 11,4cm; AD = 3,2cm.\) Phương pháp giải: Sử dụng: +) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó. Lời giải chi tiết:  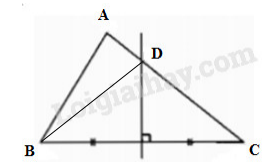 Vì \(D\) thuộc đường trung trực của \(BC\) nên \(DB = DC.\) Mặt khác, \(D\) nằm giữa \(A\) và \(C\) nên \(AD = AC – DC\) a) Nếu \(BD = 5cm; AC = 8cm,\) thì \(CD = BD = 5cm\) và \(AD = 8 – 5 = 3 (cm).\) b) \(AC = AD + DC\) \(= AD + BD = 3,2 + 11,4\) \(= 14,6 (cm).\) Loigiaihay.com
|




















Danh sách bình luận