Bài 54 trang 165 SBT toán 9 tập 1

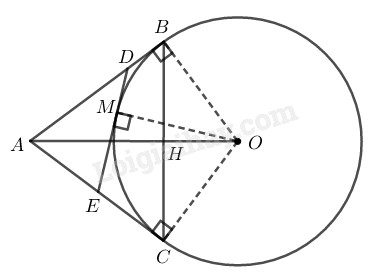
Đề bài

Cho đường tròn \((O; 3cm)\) và điểm \(A\) có \(AO = 5cm.\) Kẻ các tiếp tuyến \(AB, AC\) với đường tròn \((B, C\) là tiếp điểm\().\) Gọi \(H\) là giao điểm của \(AO\) và \(BC.\)

\(a)\) Tính độ dài \(OH.\)

\(b)\) Qua điểm \(M\) bất kì thuộc cung nhỏ \(BC,\) kẻ tiếp tuyến với đường tròn, cắt \(AB\) và \(AC\) theo thứ tự tại \(D\) và \(E.\) Tính chu vi tam giác \(ADE.\)

Lời giải chi tiết

\(a)\) Ta có: \(AB = AC\)  (tính chất hai tiếp tuyến cắt nhau).

Suy ra \(∆ABC\) cân tại A.

\(AO\) là tia phân giác của góc \(BAC\) (tính chất hai tiếp tuyến cắt nhau)

Suy ra \(AO\) là đường cao của tam giác \(ABC\) (tính chất tam giác cân).

Do đó \(AO\) vuông góc với \(BC\) tại \(H\)

Lại có: \(AB ⊥ OB\) (tính chất tiếp tuyến)

Xét tam giác \(ABO\) vuông tại \(B\) có \(BH ⊥ AO\)

Theo hệ thức lượng trong tam giác vuông, ta có:

\(O{B^2} = OH.OA \)\(\Rightarrow OH =\displaystyle  {{O{B^2}} \over {OA}}\)\( =\displaystyle {{{3^2}} \over 5} = 1,8\) (cm)

\(b)\) Áp dụng định lí Pi-ta-go vào tam giác vuông \(ABO,\) ta có:

\(A{O^2} = A{B^2} + B{O^2}\)

Suy ra: \(A{B^2} = A{O^2} - B{O^2} = {5^2} - {3^2} = 16\)

 \(\Rightarrow AB =  4 (cm)\)

Theo tính chất hai tiếp tuyến cắt nhau ta có:

\(DB = DM\)

\(EM = EC\)

Chu vi của tam giác \(ADE\) bằng:

\(AD + DE + EA \)\(= AD + DM + ME + EA\)\(= AD + DB + AE + EC\)

\(= AB + AC = 2AB\) (vì \(AB=AC\) (cmt))

\(= 2.4 = 8 (cm).\)

Loigiaihay.com