Giải bài 54 trang 100 SBT toán 10 - Cánh diều

Đề bài

Cho hình bình hành ABCD. Lấy các điểm M, N, P thoả mãn $\overrightarrow {AM}  = \frac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN}  = \frac{1}{5}\overrightarrow {AC} ,\overrightarrow {AP}  = \frac{1}{3}\overrightarrow {AD}$. Đặt $\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AD}  = \overrightarrow b$. Biểu thị các vectơ $\overrightarrow {AN} ,\overrightarrow {MN} ,\overrightarrow {NP}$ theo các vectơ $\overrightarrow a ,\overrightarrow b$ và chứng minh ba điểm M, N, P thẳng hàng.

Lời giải chi tiết

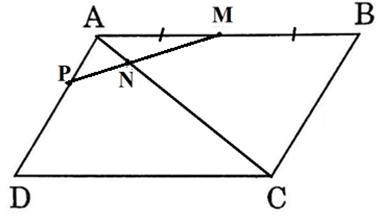
Theo giả thiết, M là trung điểm AB, N nằm giữa A và C, P nằm giữa A và D

a) Ta có:

+ $\overrightarrow {AN}  = \frac{1}{5}\overrightarrow {AC}$. Theo quy tắc hình bình hành, $\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}$ $\Rightarrow \overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right) = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)$

+ $\overrightarrow {MN}  = \overrightarrow {AN}  - \overrightarrow {AM}$mà $\overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)$, $\overrightarrow {AM}  = \frac{1}{2}\overrightarrow {AB}  = \frac{1}{2}\overrightarrow a$

nên $\overrightarrow {MN}  = \overrightarrow {AN}  - \overrightarrow {AM}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right) - \frac{1}{2}\overrightarrow a  =  - \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b$

+ $\overrightarrow {NP}  = \overrightarrow {AP}  - \overrightarrow {AN}$ mà $\overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)$, $\overrightarrow {AP}  = \frac{1}{3}\overrightarrow {AD}  = \frac{1}{3}\overrightarrow b$

nên $\overrightarrow {NP}  = \overrightarrow {AP}  - \overrightarrow {AN}  = \frac{1}{3}\overrightarrow b  - \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right) =  - \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b$

Vậy $\overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)$; $\overrightarrow {MN}  =  - \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b$; $\overrightarrow {NP}  =  - \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b$

b) Theo a, $\overrightarrow {MN}  =  - \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b$; $\overrightarrow {NP}  =  - \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b$  $\Rightarrow \overrightarrow {MN}  =  - \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b  = \frac{3}{2}\left( { - \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b } \right) = \frac{3}{2}\overrightarrow {NP}$

$\Rightarrow \overrightarrow {MN}$ và $\overrightarrow {NP}$ cùng phương. Vậy 3 điểm M, N, P thẳng hàng.