Bài 4.53 trang 121 SBT đại số 10Giải bài 4.53 trang 121 sách bài tập đại số 10. Giải các bất phương trình sau:... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
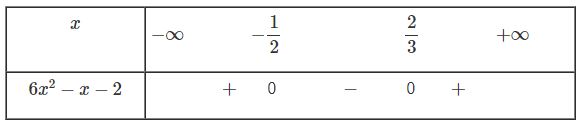
Giải các bất phương trình sau: LG a \(6{x^2} - x - 2 \ge 0;\) Phương pháp giải: - Cho \(f(x) = 0\) tìm các giá trị đặc biệt - Vẽ bảng xét dấu - Dựa vào bảng xét dấu để kết luận nghiệm Lời giải chi tiết: \(f(x) = 0\) \( \Leftrightarrow 6{x^2} - x - 2 = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \dfrac{1}{2}}\\{x = \dfrac{2}{3}}\end{array}} \right.\) Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta có \(f(x) \ge 0\)\( \Leftrightarrow x \le - \dfrac{1}{2},x \ge \dfrac{2}{3}\) LG b \({1 \over 3}{x^2} + 3x + 6 < 0.\) Phương pháp giải: - Cho \(f(x) = 0\) tìm các giá trị đặc biệt - Vẽ bảng xét dấu - Dựa vào bảng xét dấu để kết luận nghiệm Lời giải chi tiết: \(f(x) = 0\)\( \Leftrightarrow \dfrac{1}{3}{x^2} + 3x + 6 = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 3}\\{x = - 6}\end{array}} \right.\) Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta có \(f(x) < 0\) \( \Leftrightarrow x \in ( - 6; - 3)\) Tập nghiệm của bất phương trình là \( - 6 < x < - 3\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
