Bài 35 trang 108 SBT toán 9 tập 1

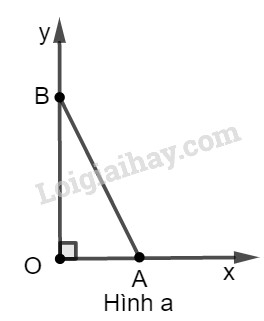
LG a

\(sin\alpha  = 0,25\);

Phương pháp giải:

Dựng góc vuông xOy.

- Vận dụng định nghĩa của các tỉ số lượng giác để nhận ra góc \(\alpha \).

- Trên tia \(Ox\) dựng đường thẳng \(OA = m\), trên tia \(Oy\) dựng đường thẳng \(OB = n\) (dựng tùy theo tỉ số lượng giác \({\rm{cos}}\alpha ; {\rm{ sin}}\alpha \) dựng đường tròn tâm A bán kính \(n\); với tỉ số lượng giác \(tg\alpha ;\cot g\alpha \) dựng cạnh \(OB = n\)).

- Nối đoạn AB.

- Chứng minh cách dựng.

Lời giải chi tiết:

\(sin\alpha  = 0,25\)

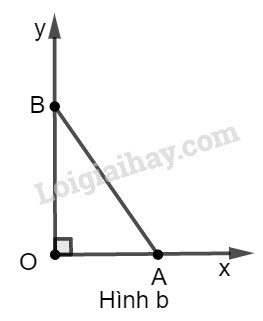
*     Cách dựng: hình a

−     Dựng góc vuông \(xOy\).

−     Trên tia \(Ox\) dựng đoạn \(OA\) bằng \(1\) đơn vị dài.

−     Dựng cung tròn tâm \(A\) bán kính \(4\) đơn vị dài và cắt \(Oy\) tại \(B\).

−     Nối AB ta được \(\widehat {OBA} = \alpha \) cần dựng.

*  Chứng minh: Ta có: \(\sin \alpha  = \sin \widehat {OBA} = \dfrac{{OA}}{ {AB}} =  \dfrac{1}{ 4} = 0,25\)

LG b

\(cos\alpha  = 0,75\) ;

Phương pháp giải:

Dựng góc vuông xOy.

- Vận dụng định nghĩa của các tỉ số lượng giác để nhận ra góc \(\alpha \).

- Trên tia \(Ox\) dựng đường thẳng \(OA = m\), trên tia \(Oy\) dựng đường thẳng \(OB = n\) (dựng tùy theo tỉ số lượng giác \({\rm{cos}}\alpha ; {\rm{ sin}}\alpha \) dựng đường tròn tâm A bán kính \(n\); với tỉ số lượng giác \(tg\alpha ;\cot g\alpha \) dựng cạnh \(OB = n\)).

- Nối đoạn AB.

- Chứng minh cách dựng.

Lời giải chi tiết:

\(cos\alpha  = 0,75\) ;

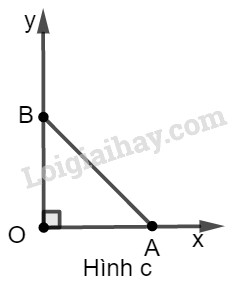
*  Cách dựng:hình b:

−     Dựng góc vuông \(xOy\).

−     Trên tia \(Ox\) dựng đoạn \(OA\) bằng \(3\) đơn vị dài.

−     Dựng cung tròn tâm \(A\) bán kính \(4\) đơn vị dài và cắt \(Oy\) tại \(B\).

−      Nối \(AB\) ta được \(\widehat {OAB} = \alpha \) cần dựng.

*     Chứng minh: Ta có: \(\cos \widehat {OAB} =  \dfrac{{OA}}{{AB}} =  \dfrac{3}{ 4} = 0,75\)

LG c

\(tg\alpha  = 1\);

Phương pháp giải:

Dựng góc vuông xOy.

- Vận dụng định nghĩa của các tỉ số lượng giác để nhận ra góc \(\alpha \).

- Trên tia \(Ox\) dựng đường thẳng \(OA = m\), trên tia \(Oy\) dựng đường thẳng \(OB = n\) (dựng tùy theo tỉ số lượng giác \({\rm{cos}}\alpha ; {\rm{ sin}}\alpha \) dựng đường tròn tâm A bán kính \(n\); với tỉ số lượng giác \(tg\alpha ;\cot g\alpha \) dựng cạnh \(OB = n\)).

- Nối đoạn AB.

- Chứng minh cách dựng.

Lời giải chi tiết:

\(tg\alpha  = 1\);

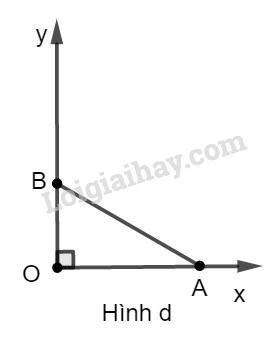
*     Cách dựng: hình c

−     Dựng góc vuông \(xOy\)

−     Trên tia \(Ox\) dựng đoạn OA bằng 1 đơn vị dài

−     Trên tia \(Oy\) dựng đoạn OB bằng 1 đơn vị dài

−     Nối AB ta được \(\widehat {OAB} = \alpha \) cần dựng

*  Chứng minh: Ta có: \(tg\alpha  = tg\widehat {OAB} =  \dfrac{{OB}}{{OA}} =  \dfrac{1}{1} = 1\)

LG d

\(\cot g\alpha  = 2.\)  

Phương pháp giải:

Dựng góc vuông xOy.

- Vận dụng định nghĩa của các tỉ số lượng giác để nhận ra góc \(\alpha \).

- Trên tia \(Ox\) dựng đường thẳng \(OA = m\), trên tia \(Oy\) dựng đường thẳng \(OB = n\) (dựng tùy theo tỉ số lượng giác \({\rm{cos}}\alpha ; {\rm{ sin}}\alpha \) dựng đường tròn tâm A bán kính \(n\); với tỉ số lượng giác \(tg\alpha ;\cot g\alpha \) dựng cạnh \(OB = n\)).

- Nối đoạn AB.

- Chứng minh cách dựng.

Lời giải chi tiết:

\(\cot g\alpha  = 2\)

*     Cách dựng: hình d

−     Dựng góc vuông \(xOy\)

−     Trên tia \(Ox\) dựng đoạn OA bằng \(2\) đơn vị dài

−     Trên tia \(Oy\) dựng đoạn OB bằng \(1\) đơn vị dài

−     Nối \(AB\) ta được \(\widehat {OAB} = \alpha \) cần dựng 

*     Chứng minh:

Ta có: \(\cot g\alpha  = \sin \widehat {OAB} =  \dfrac{{OA}}{ {OB}} =  \dfrac{2}{ 1} = 2\).

Loigiaihay.com