Bài 34 trang 42 SBT toán 7 tập 2

Đề bài

Gọi \(\displaystyle G\) là trọng tâm của tam giác \(\displaystyle ABC.\) Vẽ điểm \(\displaystyle D\) sao cho \(\displaystyle G\) là trung điểm của \(\displaystyle AD.\) Chứng minh rằng:

a) Các cạnh của tam giác \(\displaystyle BGD\) bằng \(\displaystyle \displaystyle {2 \over 3}\) các đường trung tuyến của tam giác \(\displaystyle ABC\) 

b) Các đường trung tuyến của tam giác \(\displaystyle BGD\) bằng một nửa các cạnh của tam giác \(\displaystyle ABC.\)

Lời giải chi tiết

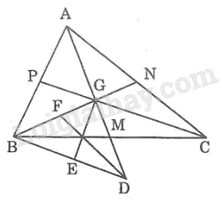
a) Gọi \(\displaystyle AM, BN, CP\) là các đường trung tuyến của \(\displaystyle ∆ABC\) cắt nhau tại \(\displaystyle G.\)

Vì \(\displaystyle AG = GD\) (vì G là trung điểm của AD)

Mà \(\displaystyle AG = 2GM\) (suy ra từ tính chất đường trung tuyến)

Nên \(\displaystyle GD  = 2GM\)

Lại có \(\displaystyle GD = GM + MD\)

Suy ra: \(\displaystyle GM = MD\)

Xét \(\displaystyle ∆BMD\) và \(\displaystyle ∆CMG:\)

+) \(\displaystyle BM = CM\) (gt) 

+) \(\displaystyle \widehat {BM{\rm{D}}} = \widehat {CMG}\) (đối đỉnh)

+) \(\displaystyle MD = GM\) (chứng minh trên)

Do đó: \(\displaystyle ∆BMD = ∆CMG\) (c.g.c)

\(\displaystyle \Rightarrow  BD = CG\)

Mà \(\displaystyle CG = {2 \over 3}CP\) (tính chất đường trung tuyến)

Suy ra: \(\displaystyle B{\rm{D = }}{2 \over 3}CP\)    (1)

\(\displaystyle BG = {2 \over 3}BN\) (tính chất đường trung tuyến)   (2)

\(\displaystyle {\rm{A}}G = {2 \over 3}AM\) (tính chất đường trung tuyến)

Suy ra: \(\displaystyle G{\rm{D}} = {2 \over 3}AM\)    (3)

Từ (1), (2) và (3) suy ra các cạnh của \(\displaystyle ∆BGD\) bằng \(\displaystyle {2 \over 3}\) các đường trung tuyến của \(\displaystyle ∆ABC.\)

b)  * Vì \(\displaystyle GM = MD\) (chứng minh trên) nên \(\displaystyle BM\) là đường trung tuyến của \(\displaystyle ∆BGD\)

Ta có \(\displaystyle BM = {1 \over 2}BC\)   (4) (vì M là trung điểm BC) 

* Kẻ đường trung tuyến \(\displaystyle GE\) và \(\displaystyle DF\) của \(\displaystyle ∆BGD\)

\(\displaystyle \Rightarrow FG = {1 \over 2}BG\) (vì F là trung điểm BG) 

\(\displaystyle GN = {1 \over 2}BG\) (tính chất đường trung tuyến)

Nên \(\displaystyle FG = GN\)

Xét \(\displaystyle ∆DFG\) và \(\displaystyle ∆ANG:\)

+) \(\displaystyle AG = GD\) (gt)

+) \(\displaystyle \widehat {DGF} = \widehat {AGN}\) (đối đỉnh)

+) \(\displaystyle GF = GN\) (chứng minh trên)

Do đó \(\displaystyle ∆DFG  = ∆ANG\) (c.g.c)

\(\displaystyle \Rightarrow  DF = AN  \)          

Mà \(\displaystyle AN = {1 \over 2}AC\) (gt)

Suy ra: \(\displaystyle {\rm{D}}F = {1 \over 2}AC\) (5)

* Ta có \(\displaystyle BD = CG\) (chứng minh câu a)

Mà \(\displaystyle {\rm{ED}} = {1 \over 2}B{\rm{D}}\) (vì \(\displaystyle E\) là trung điểm \(\displaystyle BD)\)

\(\displaystyle GP = {1 \over 2}CG\) (tính chất đường trung tuyến)

Suy ra: \(\displaystyle ED = GP\) 

Lại có \(\displaystyle ∆BDM = ∆CGM\) (chứng minh trên)

\(\displaystyle \Rightarrow \widehat {B{\rm{D}}M} = \widehat {CGM}\) hay \(\displaystyle \widehat {E{\rm{D}}G} = \widehat {CGM}\)

Mà \(\displaystyle \widehat {CGM} = \widehat {PGA}\) (đối đỉnh)

Suy ra: \(\displaystyle \widehat {{\rm{ED}}G} = \widehat {PGA}\)

Lại có: \(\displaystyle AG = GD\) (gt) và \(\displaystyle ED = GP\) (cmt)

Suy ra: \(\displaystyle ∆PGA = ∆EDG\) (c.g.c)

\(\displaystyle \Rightarrow GE = AP\) mà  \(\displaystyle AP = \dfrac{1}{2}AB\)

Suy ra: \(\displaystyle GE = {1 \over 2}AB\)             (6)

Từ (4),(5) và (6) suy ra các đường trung tuyến của \(\displaystyle ∆BGD\) bằng một nửa cạnh của \(\displaystyle ∆ABC.\)

Loigiaihay.com