Bài 37 trang 43 SBT toán 7 tập 2

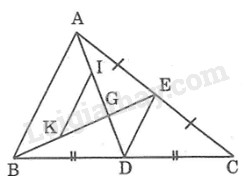
Đề bài

Theo kết quả của bài 64 chương II, SBT Toán 7 tập 1 ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Vận dụng kết quả trên để giải bài toán sau: Cho tam giác  \(\displaystyle ABC,\)  đường trung tuyến \(\displaystyle AD.\)  Kẻ đường trung tuyến \(\displaystyle BE\) cắt \(\displaystyle AD\) ở \(\displaystyle G.\) Gọi \(\displaystyle I, K\) theo thứ tự là trung điểm của \(\displaystyle GA, GB.\) Chứng minh rằng:

a) \(\displaystyle IK // DE, IK = DE\) 

b) \(\displaystyle {\rm{A}}G = {2 \over 3}A{\rm{D}}\)

Lời giải chi tiết

a) Áp dụng kết quả của bài 64 chương II sách bài tập toán 7 tập 1 vào \(\displaystyle ∆ABC\)  và vào \(\displaystyle ∆AGB\)  ta có:

+) Xét tam giác ABC có E là trung điểm AC, D là trung điểm của BC nên \(\displaystyle DE // AB\)  và \(\displaystyle {\rm{D}}E = {1 \over 2}AB\)  (1)

+) Xét tam giác GAB có I là trung điểm AG, K là trung điểm BG nên \(\displaystyle IK // AB\)  và \(\displaystyle IK = {1 \over 2}AB\)  (2)

Từ (1) và (2) suy ra:  \(\displaystyle DE // IK \) và \(\displaystyle DE = IK\) 

b) Vì \(\displaystyle AD\)  và \(\displaystyle BE\)  là 2 đường trung tuyến của \(\displaystyle ∆ABC\)  cắt nhau tại \(\displaystyle G.\) 

\(\displaystyle \Rightarrow AG = {2 \over 3}AD\) (tính chất ba đường trung tuyến)

Loigiaihay.com