Bài 39 trang 43 SBT toán 7 tập 2

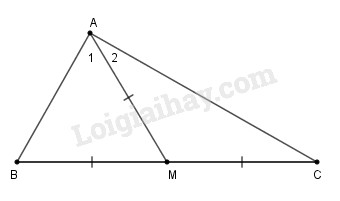
Đề bài

Tam giác \(\displaystyle ABC\) có đường trung tuyến \(\displaystyle AM\) bằng nửa cạnh \(\displaystyle BC.\) Chứng minh rằng \(\displaystyle \widehat {BAC} = 90^\circ \). 

Lời giải chi tiết

Ta có \(\displaystyle AM\) là đường trung tuyến của \(\displaystyle ∆ABC\) nên \(\displaystyle M\) là trung điểm của \(\displaystyle BC\)

\(\displaystyle \Rightarrow BM = MC = {1 \over 2}BC\)

Mà \(\displaystyle AM = {1 \over 2}BC\left( {gt} \right)\)

Suy ra: \(\displaystyle AM = BM = MC \)

Vì \(\displaystyle ∆AMB\)  có \(\displaystyle AM = MB \) nên \(\displaystyle ∆AMB\) cân tại \(\displaystyle M.\)

\(\displaystyle \Rightarrow \widehat B = \widehat {{A_1}}\) (tính chất tam giác cân)   (1)

Vì \(\displaystyle ∆AMC\) có \(\displaystyle AM = MC\) nên \(\displaystyle ∆AMC\) cân tại \(\displaystyle M.\)

\(\displaystyle \Rightarrow \widehat C = \widehat {{A_2}}\) (tính chất tam giác cân)   (2)

Từ (1) và (2) suy ra: \(\displaystyle \widehat B + \widehat C = \widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAC}\)      (3)

Trong \(\displaystyle ∆ABC\) ta có: 

\(\displaystyle \widehat B + \widehat C + \widehat {BAC} = 180^\circ \) (tổng ba góc trong tam giác)        (4)

Từ (3) và (4) suy ra: \(\displaystyle \widehat {BAC} + \widehat {BAC} = 180^\circ \)

\(\displaystyle \Rightarrow 2\widehat {BAC} = 180^\circ  \Rightarrow \widehat {BAC} = 90^\circ \)

Vậy \(\displaystyle ∆ABC\) vuông tại \(\displaystyle A.\)

Loigiaihay.com