Bài 3.34 trang 160 SBT hình học 11

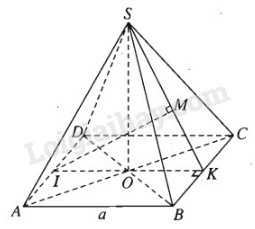
Đề bài

Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên \(SA = SB = SC = S{\rm{D}} = a\sqrt 2 \). Gọi I và K lần lượt là trung điểm của AD và BC.

a) Chứng minh mặt phẳng (SIK) vuông góc với mặt phẳng (SBC). 

b) Tính khoảng cách giữa hai đường thẳng AD và SB.

Lời giải chi tiết

a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên \(SK \bot BC\).

Ta có  

\(\left. \matrix{
BC \bot SK \hfill \cr 
BC \bot OK \hfill \cr} \right\} \Rightarrow BC \bot \left( {SIK} \right)\)

Do đó \(\left( {SBC} \right) \bot \left( {SIK} \right)\)

b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).

Theo câu a) ta có \(\left( {SIK} \right) \bot \left( {SBC} \right)\) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức \(IM.SK = SO.IK\), ta có \(IM = {{SO.IK} \over {SK}}\).

Ta lại có: \(S{K^2} = S{B^2} - B{K^2} = 2{{\rm{a}}^2} - {{{a^2}} \over 4} = {{7{a^2}} \over 4} \Rightarrow SK = {{a\sqrt 7 } \over 2}\)

Và \(S{O^2} = S{A^2} - O{A^2} = 2{{\rm{a}}^2} - {\left( {{{a\sqrt 2 } \over 2}} \right)^2} = {{3{{\rm{a}}^2}} \over 2}\)

\(\Rightarrow SO = {{a\sqrt 3 } \over {\sqrt 2 }} = {{a\sqrt 6 } \over 2}\)

Do đó: \(IM = {{SO.IK} \over {SK}} = {{a\sqrt 6 } \over 2}.a:{{a\sqrt 7 } \over 2} = {{a\sqrt {42} } \over 7}\)

Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng \({{a\sqrt {42} } \over 7}\).

Loigiaihay.com