Bài 3.36 trang 160 SBT hình học 11

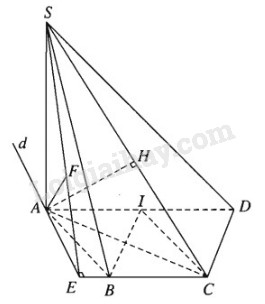
Đề bài

Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính AD = 2a và có cạnh SA vuông góc với mặt phẳng đáy (ABCD) với \(SA = a\sqrt 6 \).

a) Tính khoảng cách từ A và B đến mặt phẳng (SCD).

b) Tính khoảng cách từ  đường thẳng AD đến mặt phẳng (SBC)

Lời giải chi tiết

a) Vì ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a nên ta có: \(A{\rm{D}}\parallel BC\) và \(AB = BC = C{\rm{D}} = a\), đồng thời \(AC \bot C{\rm{D}},AB \bot B{\rm{D}},AC = B{\rm{D}} = a\sqrt 3 \).

Như vậy

\(\left. \matrix{
C{\rm{D}} \bot AC \hfill \cr 
C{\rm{D}} \bot SA \hfill \cr} \right\} \Rightarrow C{\rm{D}} \bot \left( {SAC} \right)\)

Trong mặt phẳng (SAC) dựng AH ⊥ SC tại H ta có AH ⊥ CD và AH ⊥ SC nên AH ⊥ (SCD)

Vậy AH = d(A,(SCD))

Xét tam giác SAC vuông tại A có AH là đường cao, ta có:

\(\eqalign{
& {1 \over {A{H^2}}} = {1 \over {S{A^2}}} + {1 \over {A{C^2}}} \cr 
& = {1 \over {{{\left( {a\sqrt 6 } \right)}^2}}} + {1 \over {{{\left( {a\sqrt 3 } \right)}^2}}} = {1 \over {2{{\rm{a}}^2}}} \cr} \)

Vậy \(A{H^2} = 2{{\rm{a}}^2} \Rightarrow AH = a\sqrt 2 \)

Gọi I là trung điểm của AD ta có \(BI\parallel C{\rm{D}}\) nên BI song song với mặt phẳng (SCD). Từ đó suy ra \(d\left( {B,\left( {SC{\rm{D}}} \right)} \right) = d\left( {I,\left( {SC{\rm{D}}} \right)} \right)\).

Mặt khác AI cắt (SCD) tại D nên

\(d\left( {I,\left( {SC{\rm{D}}} \right)} \right) = {1 \over 2}d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = {1 \over 2}.a\sqrt 2  = {{a\sqrt 2 } \over 2}\)

Do đó: \(d\left( {B,\left( {SC{\rm{D}}} \right)} \right) = {{a\sqrt 2 } \over 2}\)

b) Vì \(AD\parallel BC\) nên \(AD\parallel \left( {SBC} \right)\), do đó \(d\left( {AD,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\)

Dựng \(AD \bot BC\) tại \(E \Rightarrow BC \bot \left( {SA{\rm{E}}} \right)\)

Dựng \(AD \bot SE\) tại F ta có:

\(\left. \matrix{
AF \bot SE \hfill \cr 
AF \bot BC\,\left( {vì\,BC \bot \left( {SAE} \right)} \right) \hfill \cr} \right\} \Rightarrow AF \bot \left( {SBC} \right)\)

Vậy \(AF = d\left( {A,\left( {SBC} \right)} \right) = d\left( {AD,\left( {SBC} \right)} \right)\)

Xét tam giác vuông AEB ta có: \(AE = AB\sin \widehat {ABE} = a\sin {60^0} = {{a\sqrt 3 } \over 2}\)

Xét tam giác SAE vuông tại A ta có:

\({1 \over {A{F^2}}} = {1 \over {S{A^2}}} + {1 \over {A{E^2}}} = {1 \over {{{\left( {a\sqrt 6 } \right)}^2}}} + {1 \over {\left( {{{a\sqrt 3 } \over 2}} \right)}} = {9 \over {6{a^2}}}\) 

Do đó \(A{F^2} = {{6{a^2}} \over 9} \Rightarrow AF = {{a\sqrt 6 } \over 3}\)

Vậy \(d\left( {AD,\left( {SBC} \right)} \right) = AF = {{a\sqrt 6 } \over 3}\)

Loigiaihay.com