Bài 3.39 trang 160 SBT hình học 11Giải bài 3.39 trang 160 sách bài tập hình học 11. Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC... Quảng cáo
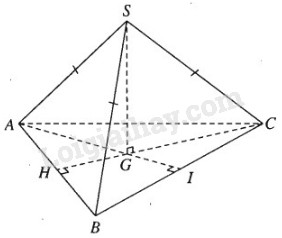
Đề bài Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC. a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC). b) Tính khoảng cách giữa hai đường thẳng AB và SG Lời giải chi tiết
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có \(\eqalign{ Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a b) Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó \(HG = {1 \over 3}HC\) mà \(HC = {{3{\rm{a}}\sqrt 3 } \over 2}\) nên \(HG = {{a\sqrt 3 } \over 2}\). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
