Bài 33 trang 42 SBT toán 7 tập 2

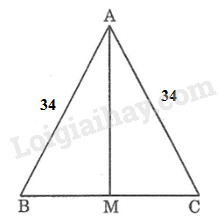
Đề bài

Tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 34cm, BC = 32cm.\) Kẻ đường trung tuyến \(AM.\)

a) Chứng minh rằng \(AM \bot BC\)

b) Tính độ dài \(AM.\) 

Lời giải chi tiết

a) Xét \(∆AMB\) và \(∆AMC:\)

+) \(AB = AC\) (gt)

+) \(BM = CM \) (vì M là trung điểm BC)

+) \(AM\) cạnh chung

Do đó: \(∆AMB = ∆AMC\) (c.c.c)

\( \Rightarrow \widehat {AMB} = \widehat {AMC}\) (1)

Ta có: \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù) (2)

Từ (1) và (2) suy ra: \(\widehat {AMB} = \widehat {AMC} \)\(=180^0:2= 90^\circ \)

Vậy: \(AM \bot BC\)

b) Xét tam giác vuông \(AMB\) ta có: \(\widehat {AMB} = 90^\circ \)

Theo định lý Pytago ta có:

\(\eqalign{
& \,\,\,\,A{B^2} = A{M^2} + B{M^2} \cr 
& \Rightarrow A{M^2} = A{B^2} - B{M^2} \cr 
&\Rightarrow AM^2= {34^2} - {16^2} \cr 
&\Rightarrow A{M^2} = 1156 - 256 = 900 \cr 
& \Rightarrow AM = 30\left( {cm} \right) \cr} \)

Loigiaihay.com