Bài 3.24 trang 150 SBT hình học 11

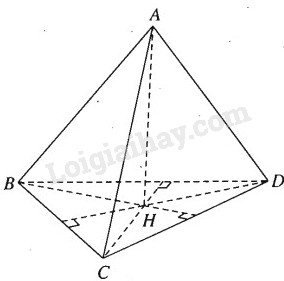
Đề bài

Chứng minh rằng nếu tứ diện ABCD có \(AB \bot C{\rm{D}}\) và \(AC \bot B{\rm{D}}\) thì \(AD \bot BC\).

Lời giải chi tiết

Vẽ \(AH \bot \left( {BC{\rm{D}}} \right)\) tại H, ta có \(C{\rm{D}} \bot AH\) và vì \(C{\rm{D}} \bot AB\) ta suy ra \(C{\rm{D}} \bot BH\). Tương tự vì \({\rm{BD}} \bot AC\) ta suy ra \({\rm{BD}} \bot CH\)

Vậy H  là trực tâm của tam giác BCD  tức là \(DH \bot BC\)

Vì \(AH \bot BC\) nên ta suy ra \(BC \bot A{\rm{D}}\)

Cách khác . Trước hết ta hãy chứng minh hệ thức:

\(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}}  + \overrightarrow {AC} .\overrightarrow {DB}  + \overrightarrow {{\rm{AD}}} .\overrightarrow {BC}  = 0\) với bốn điểm A, B, C, D bất kì.

Thực vậy , ta có:

\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = \overrightarrow {AB} .\left( {\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} .\overrightarrow {AB} \,\,\,\,\,\,\,\left( 1 \right) \cr 
& \overrightarrow {AC} .\overrightarrow {DB} = \overrightarrow {AC} .\left( {\overrightarrow {AB} - \overrightarrow {{\rm{AD}}} } \right) = \overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AC} .\overrightarrow {{\rm{AD}}} \,\,\,\,\,\,\left( 2 \right) \cr 
& \overrightarrow {{\rm{AD}}} .\overrightarrow {BC} = \overrightarrow {{\rm{AD}}} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \overrightarrow {{\rm{AD}}} .\overrightarrow {AC} - \overrightarrow {{\rm{AD}}} .\overrightarrow {AB} \,\,\,\,\,\,\,\left( 3 \right) \cr} \)

\(\left( 1 \right) + \left( 2 \right) + \left( 3 \right) \Leftrightarrow \overrightarrow {AB} .\overrightarrow {C{\rm{D}}}  + \overrightarrow {AC} .\overrightarrow {DB}  + \overrightarrow {AD} .\overrightarrow {BC}  = 0\,\,\,\,\,\,\left( 4 \right)\) 

Do đó nếu \(AB \bot CD\) nghĩa là \(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}}  = 0\,\,\), \(AC \bot BD\) nghĩa là \(\overrightarrow {AC} .\overrightarrow {B{\rm{D}}}  = 0\,\,\)

Từ hệ thức (4) ta suy ra \(\overrightarrow {AD} .\overrightarrow {BC}  = 0\,\,\), do đó \(A{\rm{D}} \bot BC\).

 Loigiaihay.com