Bài 3.27 trang 151 SBT hình học 11

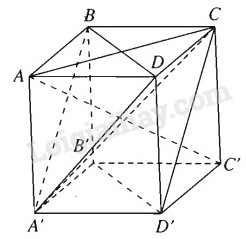
Đề bài

a) Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).

b) Tính đường chéo AC’ của hình lập phương đã cho.

Lời giải chi tiết

a) Ta có \(AB = A{\rm{D}} = AA' = a\)

và \(C'B = C'D = C'A' = a\sqrt 2 \)

Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy \(AC' \bot \left( {B{\rm{D}}A'} \right)\).

Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà \(AC' \bot \left( {B{\rm{D}}A'} \right)\) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng  (BDA’)

b) Ta có ACC’ là tam giác vuông có cạnh \(AC = a\sqrt 2 \) và CC’ = a

Vậy \(AC{'^2} = A{C^2} + CC{'^2} \Rightarrow AC{'^2} = 2{{\rm{a}}^2} + {a^2} = 3{{\rm{a}}^2}\)

Vậy \(AC' = a\sqrt 3 \).

Loigiaihay.com