Bài 2.51 trang 104 SBT hình học 10

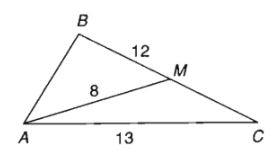
LG a

Tính diện tích tam giác ABC;

Phương pháp giải:

- Tính diện tích tam giác \(AMC\) theo công thức Hê – rông \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)

- Từ đó suy ra diện tích tam giác \(ABC\).

Lời giải chi tiết:

Ta có: BM=MC=6

Nửa chu vi tam giác AMC là: \(p = \frac{{AM + MC + CA}}{2}\) \(= \frac{{8 + 6 + 13}}{2} = \frac{{27}}{2}\)

Theo công thức Hê – rông ta có:

\({S_{AMC}} = \sqrt {\dfrac{{27}}{2}\left( {\dfrac{{27}}{2} - 13} \right)\left( {\dfrac{{27}}{2} - 6} \right)\left( {\dfrac{{27}}{2} - 8} \right)} \)\( = \dfrac{{9\sqrt {55} }}{4}\)

\({S_{ABC}} = 2{S_{AMC}} = \dfrac{{9\sqrt {55} }}{2}\).

LG b

Tính góc B.

Phương pháp giải:

Sử dụng công thức trung tuyến \(A{M^2} = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\) tính cạnh còn lại của tam giác.

Sử dụng định lý cô sin trong tam giác tính góc \(B\).

Lời giải chi tiết:

Ta có \(A{M^2} = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\) hay \(2A{M^2} = {b^2} + {c^2} - \dfrac{{{a^2}}}{2}\).

Do đó \(A{B^2} = {c^2} = 2A{M^2} - {b^2} + \dfrac{{{a^2}}}{2}\)\( = 2.64 - 169 + 72 = 31\) \( \Rightarrow c = \sqrt {31} \)

\(\cos B = \dfrac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)\( = \dfrac{{144 + 31 - 169}}{{24\sqrt {31} }} \approx 0,045\) \( \Rightarrow \widehat B \approx {87^0}25'\)

Loigiaihay.com