Giải bài 2.5 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức

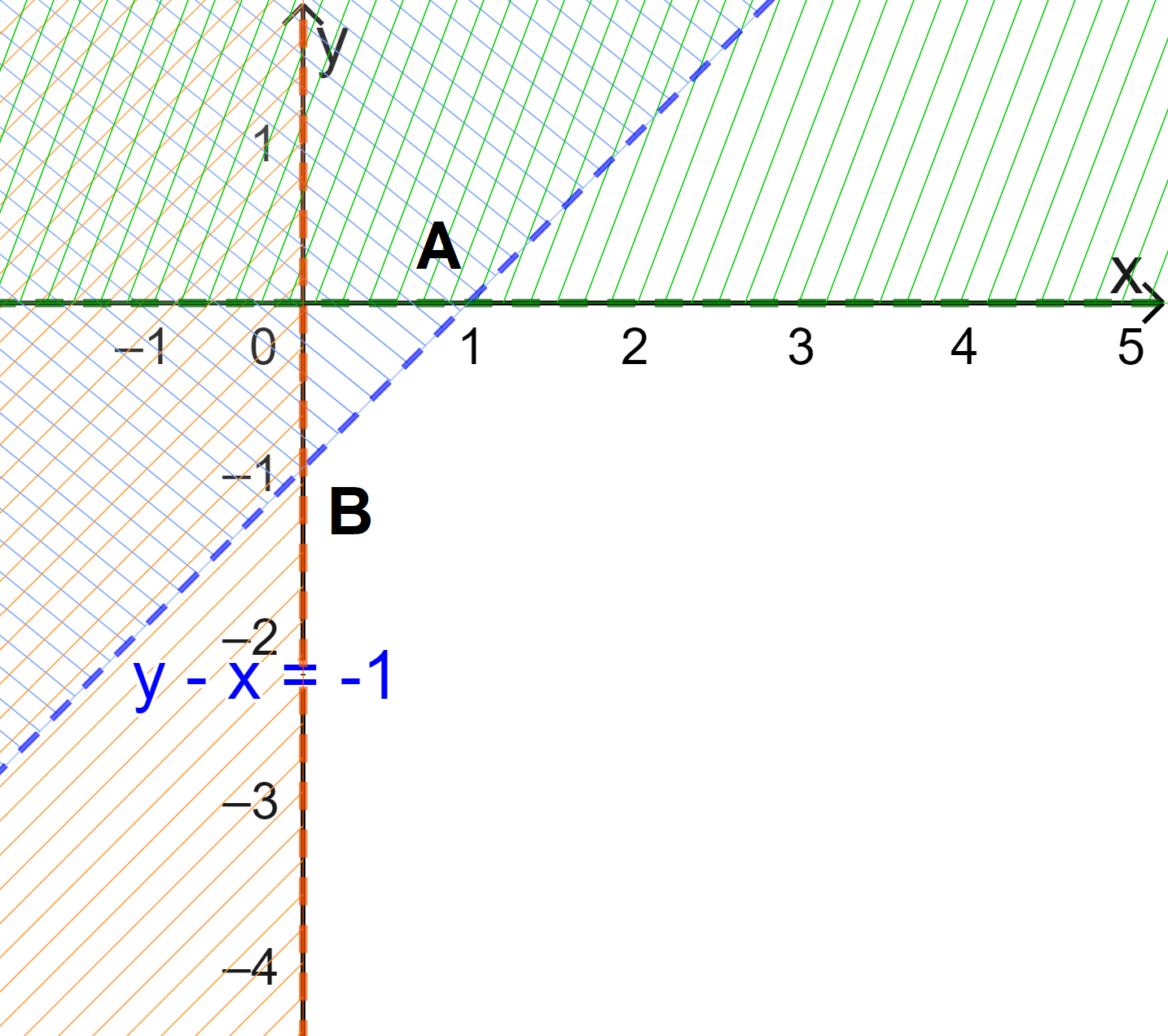
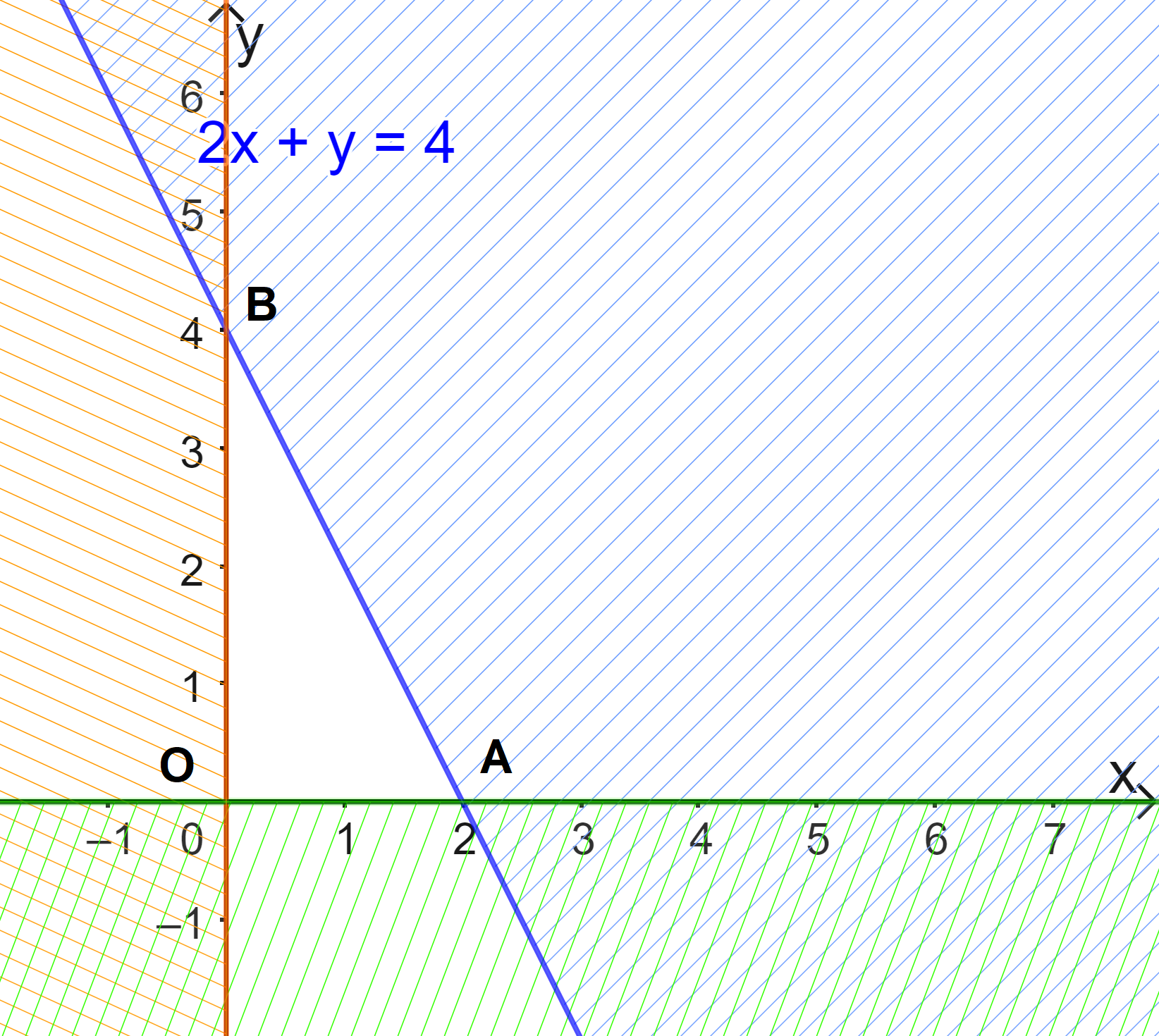
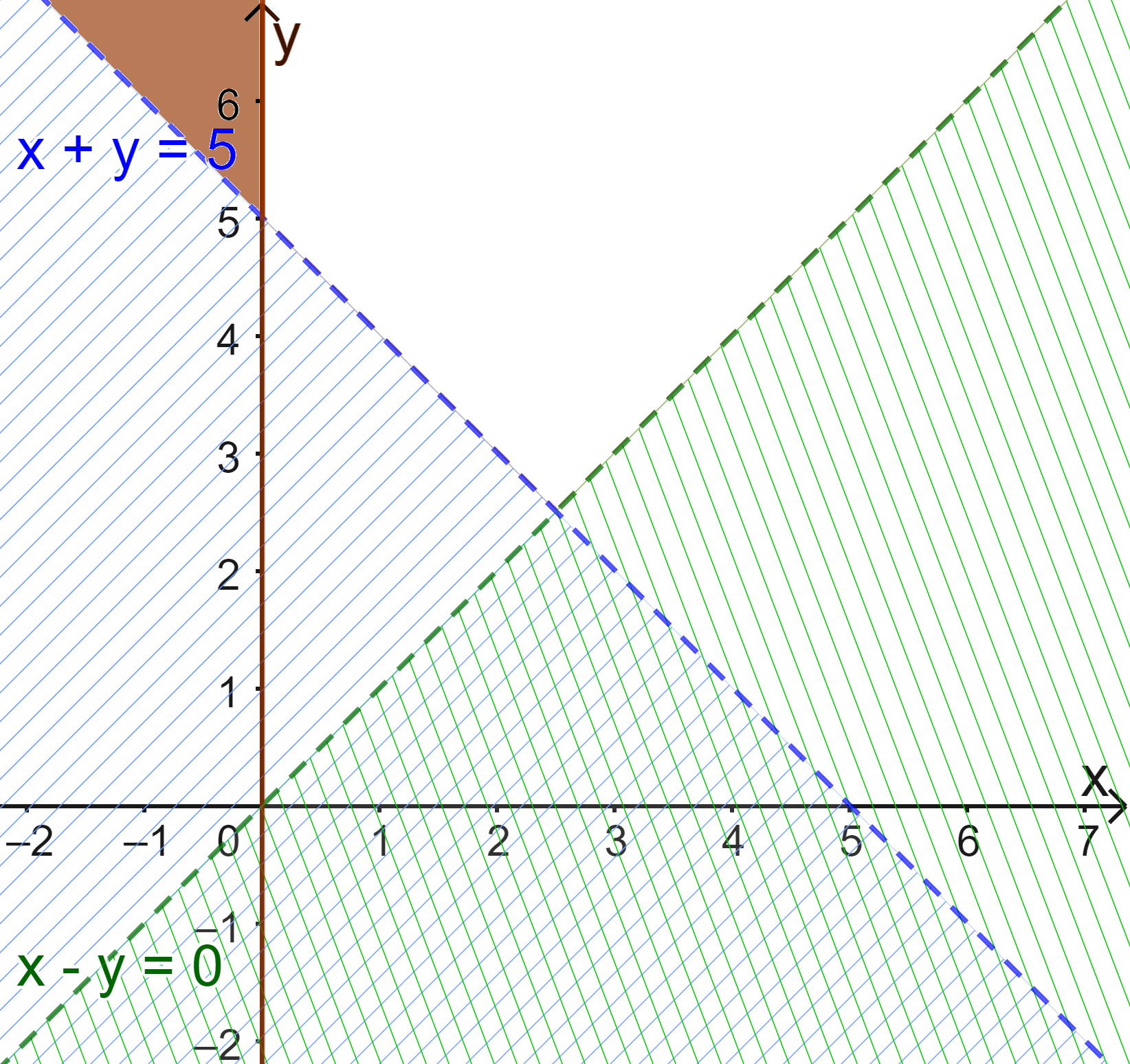
Đề bài

Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:

a) \(\left\{ \begin{array}{l}y - x <  - 1\\x > 0\\y < 0\end{array} \right.\)

b) \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y \le 4\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x \ge 0\\x + y > 5\\x - y < 0\end{array} \right.\)

Lời giải chi tiết

a)

Xác định miền nghiệm của BPT \(y - x <  - 1\)

+ Vẽ đường thẳng d: \(y-x=  - 1\) đi qua A(1;0) và B(0;-1)

+ Vì \(0-0= 0 > - 1\) nên tọa độ điểm O(0;0) không thỏa mãn BPT \(y - x <  - 1\)

Do đó, miền nghiệm của BPT \(y - x <  - 1\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.

Miền nghiệm của BPT \(x > 0\) là nửa mặt phẳng bên phải Oy (không kể trục Oy).

Miền nghiệm của BPT \(y < 0\) là nửa mặt phẳng dưới Ox (không kể trục Ox).

Khi đó miền nghiệm của hệ bất phương trình đã cho là miền không gạch (Không kể đoạn thẳng AB và các trục tọa độ).

 

b)

Miền nghiệm của BPT \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0) (kể cả trục Oy).

Miền nghiệm của BPT \(y \ge 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) (kể cả trục Ox).

Xác định miền nghiệm của bất phương trình \(2x + y \le 4\)

+ Vẽ đường thẳng d: \(2x + y = 4\) đi qua A(2;0) và B(0;4)

+ Vì \(2.0 + 0 = 0 < 4\) nên tọa độ điểm O(0;0) thỏa mãn BPT \(2x + y \le 4\)

Do đó, miền nghiệm của bất phương trình \(2x + y \le 4\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.

Vậy miền nghiệm của hệ bất phương trình đã cho là miền tam giác OAB (kể cả các đoạn thẳng OA, OB, AB).

 

c)

Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bên phải Oy (kể cả trục Oy).

Xác định miền nghiệm của bất phương trình \(x + y > 5\)

+ Vẽ đường thẳng d: \(x + y = 5\)

+ Vì \(0 + 0 = 0 < 5\) nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình \(x + y > 5\).

Do đó, miền nghiệm của BPT \(x + y > 5\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.

Xác định miền nghiệm của bất phương trình \(x - y < 0\)

+ Vẽ đường thẳng d: \(x - y = 0\)

+ Vì \(1 - 0 = 1 > 0\) nên tọa độ điểm (1;0) không thỏa mãn bất phương trình \(x - y < 0\)

Do đó, miền nghiệm của bất phương trình \(x - y < 0\) là nửa mặt phẳng bờ d’ không chứa điểm (1;0).

Vậy miền nghiệm của hệ bất phương trình đã cho là miền màu trắng (không kể d và d’)