Bài 2.37 trang 102 SBT hình học 10

Đề bài

Chứng minh rằng diện tích hình bình hành bằng tích hai cạnh liên tiếp với \(\sin \) của góc xen giữa chúng.

Lời giải chi tiết

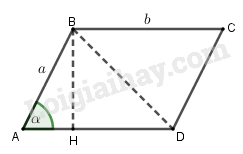
Xét hình bình hành ABCD có \(AB = a,AD = b,\widehat {BAD} = \alpha \) và BH là đường cao, ta có \(BH \bot AD\) tại H.

Gọi S là diện tích hình bình hành ABCD, ta có S = AD. BH với \(BH = AB\sin \alpha \)

Vậy \(S = AD.AB\sin \alpha  = a.b.\sin \alpha \)

Nếu \(\widehat {BAD} = \alpha \) thì \(\widehat {ABC} = {180^0} - \alpha \)

Khi đó ta vẫn có \(\sin \widehat {BAD} = \sin \widehat {ABC}\)

Nhận xét: 

Diện tích hình bình hành ABCD gấp đôi diện tích tam giác ABD mà tam giác ABD có diện tích là \(\dfrac{1}{2}ab\sin \alpha \).

Do đó ta suy ra diện tích của hình bình hành bằng \(ab\sin \alpha \).

Loigiaihay.com