Bài 2.23 trang 76 SBT hình học 11

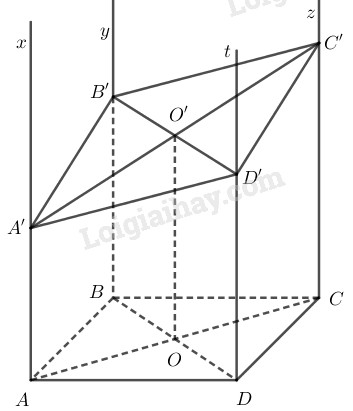
LG a

Chứng minh rằng \(\left( {Ax,By} \right)\parallel \left( {Cz,Dt} \right)\) và \(\left( {Ax,Dt} \right)\parallel \left( {By,Cz} \right)\).

Phương pháp giải:

Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với \(d’\) nằm trong \((\alpha)\) thì \(d\) song song với \((\alpha)\).

\(\left\{ \begin{array}{l}d \not\subset (\alpha )\\d\parallel d'\\d' \subset (\alpha )\end{array} \right. \Rightarrow d\parallel (\alpha )\)

Sử dụng tính chất: Nếu mặt phẳng \((\alpha)\) chứa hai đường thẳng cắt nhau \(a, b\) và hai đường thẳng này cùng song song với mặt phẳng \((\beta)\) thì mặt phẳng \((\alpha)\) song song với mặt phẳng \((\beta)\).

\(\left\{ \begin{array}{l}a \subset (\alpha ),b \subset (\alpha )\\a\text{ cắt }b\\a\parallel (\beta ),b\parallel (\beta )\end{array} \right. \Rightarrow (\alpha )\parallel (\beta )\)

Lời giải chi tiết:

Ta có:

\(\left\{ \begin{array}{l}{\rm{Ax}}\parallel Dt\\Dt \subset (Cz,Dt)\end{array} \right. \Rightarrow {\rm{Ax}}\parallel (Cz,Dt)\)

\(\left\{ \begin{array}{l}{\rm{AB}}\parallel CD\\CD \subset (Cz,Dt)\end{array} \right. \Rightarrow {\rm{AB}}\parallel (Cz,Dt)\)

Mà \(Ax, AB \subset (Ax, By)\) suy ra \((Ax, By)\parallel (Cz, Dt)\)

Chứng minh tương tự \((Ax, Dt)\parallel (By, Cz)\).

LG b

Tứ giác \(A’B’C’D’\) là hình gì?

Phương pháp giải:

Sử dụng tính chất: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}(\alpha ) \cap ({\rm{Ax,By}}) = A'B'\\(\alpha ) \cap (Cz{\rm{,Dt}}) = C'D'\\({\rm{Ax,By}})\parallel (Cz{\rm{,Dt}})\end{array} \right. \)

\(\Rightarrow A'B'\parallel C'D'\) \(\text{  (1)}\)

\(\left\{ \begin{array}{l}(\alpha ) \cap ({\rm{Ax,Dt}}) = A'D'\\(\alpha ) \cap (By,Cz) = B'C'\\({\rm{Ax,Dt}})\parallel (By,Cz)\end{array} \right. \)

\(\Rightarrow A'D'\parallel B'C'\) \(\text{  (2)}\)

Từ \(\text{(1)}\) và \(\text{(2)}\) suy ra tứ giác \(A’B’C’D’\) là hình bình hành.

LG c

Chứng minh \(AA' + CC' = BB' + DD'\)

Phương pháp giải:

Sử dụng tính chất đường trung bình của hình thang.

Lời giải chi tiết:

Gọi \(O, O’\) lần lượt là tâm của hình bình hành \(ABCD\), \(A’B’C’D’\).

Ta có \(O\) là trung điểm của \(AC\), \(O’\) là trung điểm của \(A’C’\) nên \(OO’\) là đường trung bình của hình thang \(ACC’A’\)

Suy ra \(OO’=\dfrac{AA’+CC’}{2}\) \(\text (1)\).

Tương tự \(O\) là trung điểm của \(BD\), \(O’\) là trung điểm của \(B’D’\) nên \(OO’\) là đường trung bình của hình thang \(BDD’B’\)

Suy ra \(OO’=\dfrac{BB’+DD’}{2}\) \(\text (2)\).

Từ \(\text (1)\) và \(\text (2)\) suy ra \(AA’+CC’=BB+DD’\).

Loigiaihay.com