Bài 2.26 trang 77 SBT hình học 11

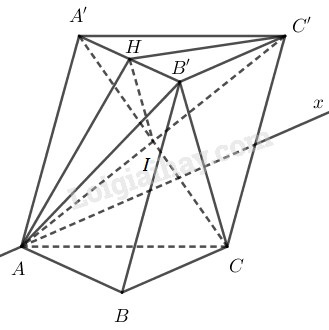
LG a

Chứng minh rằng \(CB'\parallel \left( {AHC'} \right)\).

Phương pháp giải:

Trong bài này muốn chứng minh đường thẳng song song với mặt phẳng ta chứng minh đường thẳng đó song song với một đường thẳng thuộc mặt phẳng.

\(\left\{ \begin{array}{l}d \not\subset (\alpha )\\d\parallel d'\\d' \subset (\alpha )\end{array} \right. \Rightarrow d\parallel (\alpha )\)

Sử dụng tính chất của hình bình hành, tính chất của đường trung bình.

Lời giải chi tiết:

Gọi \(I=A’C\cap AC’\) do tứ giác \(A’ACC’\) là hình bình hành nên \(I\) là trung điểm của \(A’C\).

Trong tam giác \(A’B’C\) có \(I\) là trung điểm của \(A’C\) và \(H\) là trung điểm của \(A’B’\) nên \(IH\) là đường trung bình của tam giác.

Suy ra \(IH\parallel B’C\)

Mà \(IH\subset (AHC’)\)

Suy ra \(B’C\parallel (AHC’)\).

LG b

Tìm giao tuyến \(d\) của \((AB’C’)\) và \((ABC)\)

Phương pháp giải:

Sử dụng tính chất: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Cách tìm giao tuyến của hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song.

- Tìm điểm chung của hai mặt phẳng.

- Qua điểm chung vẽ đường thẳng song song với hai đường thẳng song song đó.

Lời giải chi tiết:

Ta có:

\(\left\{ \begin{array}{l}A \in (AB'C') \cap (ABC)\\B'C' \subset (AB'C')\\BC \subset (ABC)\\B'C'\parallel BC\end{array} \right. \)

\(\Rightarrow (AB'C') \cap (ABC) = d = {\rm{Ax}}\),

\({\rm{Ax}}\parallel B'C'\parallel BC\).

Loigiaihay.com