Bài 20 trang 105 SBT toán 9 tập 1Giải bài 20 trang 105 sách bài tập toán 9. Cho tam giác vuông ABC. Từ một điểm M bất kì trong tam giác kể MD, ME, MF lần lượt vuông góc với các cạnh BC, AC, AB Quảng cáo
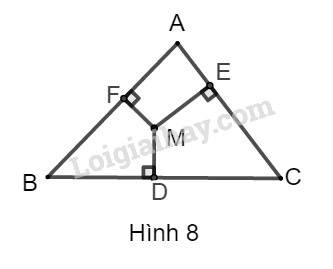
Đề bài Cho tam giác vuông \(ABC\). Từ một điểm M bất kì trong tam giác kẻ \(MD, ME, MF\) lần lượt vuông góc với các cạnh \(BC, AC, AB\). Chứng minh rằng: \(B{D^2} + C{E^2} + A{F^2} = D{C^2} + E{A^2} + F{B^2}.\)
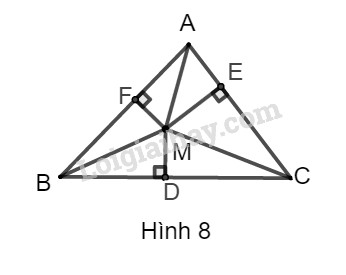
Phương pháp giải - Xem chi tiết - Vẽ hình phụ tạo thành các tam giác vuông (với bài toán này ta nối các điểm tạo thành các cạnh \(AM, BM, CM\)). - Xét các tam giác vuông, sử dụng định lý Pytago tạo thành các đẳng thức phù hợp. - Tìm mối liên hệ giữa các đẳng thức vừa được tạo thành và đẳng thức cần được chứng minh của bài toán. Sử dụng: Định lý Pytago: Cho tam giác \(ABC\) vuông tại \(A,\) ta có: \(B{C^2} = A{B^2} + A{C^2}\) Lời giải chi tiết Nối \(AM, CM, BM\) ta được hình dưới đây:
Áp dụng định lí Pytago vào tam giác vuông \(BDM\), ta có: \(B{M^2} = B{D^2} + D{M^2}\)\( \Rightarrow B{D^2} = B{M^2} - D{M^2}\) (1) Áp dụng đinh lí Pytago vào tam giác vuông \(CEM\), ta có: \(C{M^2} = C{E^2} + E{M^2}\)\( \Rightarrow C{E^2} = C{M^2} - E{M^2}\) (2) Áp dụng định lí Pytago vào tam giác vuông \(AFM\), ta có: \(A{M^2}{\rm{ = A}}{{\rm{F}}^2} + F{M^2}\)\( \Rightarrow A{F^2} = A{M^2} - F{M^2}\) (3) Cộng từng vế của (1), (2) và (3) ta có: \(B{D^2} + C{E^2} + A{F^2}\) \(= B{M^2} - D{M^2} + C{M^2}\)\( - E{M^2} + A{M^2} - F{M^2}\) (4) Áp dụng định lí Pytago vào tam giác vuông \(BFM\), ta có: \(B{M^2} = B{F^2} + F{M^2}\) (5) Áp dụng định lí Pytago vào tam giác vuông \(CDM\), ta có: \(C{M^2} = C{D^2} + D{M^2}\) (6) Áp dụng định lí Pytago vào tam giác vuông \(AEM\), ta có: \(A{M^2} = A{E^2} + E{M^2}\) (7) Thay (5), (6), (7) vào (4) ta có: \(\eqalign{ Vậy \(B{D^2} + C{E^2}{\rm{ + A}}{{\rm{F}}^2} = D{C^2} + E{A^2} + F{B^2}.\) Loigiaihay.com
|




















Danh sách bình luận