Bài 1.3 phần bài tập bổ sung trang 105 SBT toán 9 tập 1

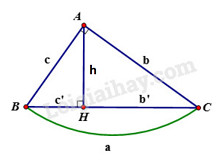
Đề bài

Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH :\) \(AB = c, AC = b, BC = a,\)\( AH = h, BH = c', CH = b'.\)

a)  Tính \(h, b, c\) nếu biết \(b' = 36, c' = 64\).

b)  Tính \(h, b, b', c'\) nếu biết \(a = 9, c = 6\).  

Lời giải chi tiết

 

a) Áp dụng các hệ thức lượng trong tam giác vuông ta có: 

Ta có  

\(\begin{array}{l}
{h^2} = b'.c' = 36.64 = 2304\\
\Rightarrow h = 48
\end{array}\)

\(\begin{array}{l}
{b^2} =b'.a= b'(b' + c') \\= 36.(36 + 64) = 3600\\
\Rightarrow b = 60
\end{array}\) 

\(\begin{array}{l}
{c^2}=c'.a = c'(b' + c') \\= 64.(36 + 64) = 6400\\
\Rightarrow c = 80
\end{array}\)

b) Áp dụng các hệ thức lượng trong tam giác vuông ta có: 

+ \(c^2=c'.a\)

\(\Rightarrow c' = \dfrac{{{c^2}}}{a} = \dfrac{{{6^2}}}{9} = 4\),

+ \(b' = a - c' = 9 - 4 = 5\),

+ \({b^2} = a.b' = 9 . 5 = 45\) nên \(b = 3\sqrt 5\);

+ \({h^2} = b'.c' = 5.4=20\) nên \(h = 2\sqrt 5 \).

Loigiaihay.com