Bài 2 trang 201 SBT Hình học 10

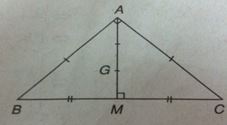
Đề bài

Trong mặt phẳng  Oxy cho tam giác ABC có \(AB = AC,\,\widehat {BAC} = {90^ \circ }\). Biết M(1 ; -1) là trung điểm cạnh BC và \(G\left( {\frac{2}{3};0} \right)\) là trọng tâm tam giác ABC. Tìm tọa độ các đỉnh A, B, C.

Lời giải chi tiết

\(\overrightarrow {MA}  = 3\overrightarrow {MG}  \Leftrightarrow \left\{ \begin{array}{l}{x_A} - 1 = 3\left( {\frac{2}{3} - 1} \right)\\{y_A} + 1 = 3(0 + 1)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 0\\{y_A} = 2.\end{array} \right.\)

Vậy A có tọa độ (0 ; 2).

Đặt B(x ; y) ta có :

\(\begin{array}{l}\,\,\,\,\,\,\,\left\{ \begin{array}{l}\overrightarrow {MB}  \bot \overrightarrow {MA} \\M{B^2} = M{A^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {0 - 1} \right) + \left( {y + 1} \right)\left( {2 + 1} \right) = 0\\{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 1 + 9\end{array} \right.\end{array}\)

\( \Leftrightarrow \left\{ \begin{array}{l}x = 3y + 4\\{(3y + 3)^2} + {(y + 1)^2} = 10\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x = 3y + 4\\{(3y + 3)^2} + {(y + 1)^2} = 10\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}x = 3y + 4\\10{y^2} + 20y = 0\end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}y = 0,x = 4\\y =  - 2,x =  - 2\end{array} \right.\)

Vậy ta có tọa độ của điểm B và C như sau : B(4 ; 0), C(-2 ; -2) hoặc B(-2 ; -2), C(4 ; 0).

Loigiaihay.com