Bài 2 trang 156 SBT toán 9 tập 1

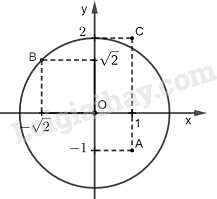
Đề bài

Trên mặt phẳng tọa độ $Oxy$,  hãy xác định vị trí tương đối của mỗi điểm:

$A( 1 ; -1)$, $B( - \sqrt 2 ;\sqrt 2 )$ và $C( 1 ; 2)$ đối với đường tròn $(O ; 2 )$. 

Lời giải chi tiết

Gọi $R$ là bán kính của đường tròn $(O ; 2).$ Ta có $R = 2$

$O{A^2} = {1^2} + {1^2} = 2 \Rightarrow OA = \sqrt 2  < 2$

Vì $OA < R$ nên điểm $A$ nằm trong đường tròn $(O; 2)$

$\eqalign{ & O{B^2} = {(\sqrt 2 )^2} + {(\sqrt 2 )^2} \cr  & = 2 + 2 = 4 \Rightarrow OB = 2 \cr}$

Vì $OB = R$ nên điểm $B$ thuộc đường tròn $(O; 2)$

$\eqalign{ & O{C^2} = {1^2} + {2^2} = 1 + 4 = 5 \cr  & \Rightarrow OC = \sqrt 5 > 2 \cr}$

Vì $OC > R$ nên điểm $C$ nằm ngoài đường tròn $(O; 2).$

Loigiaihay.com