Bài 1.86 trang 48 SBT hình học 10

Đề bài

Cho ba điểm không thẳng hàng \(A,B,C\). Điểm \(D\) là đỉnh thứ tư của hình bình hành \(ABDC\) khi và chỉ khi:

A. \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \)

B. \(\overrightarrow {AC}  = \overrightarrow {BD} \)

C. \(\overrightarrow {DB}  - \overrightarrow {DC}  = \overrightarrow {CB} \)

D. \(\overrightarrow {OA}  + \overrightarrow {OD}  = \overrightarrow 0 \), \(O\) là trung điểm của \(BC\).

Hãy chọn khẳng định sai.

Lời giải chi tiết

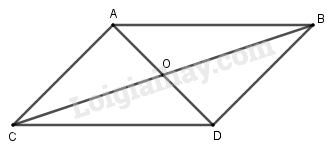
\(ABDC\) là hình bình hành \( \Leftrightarrow \) \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \) nên A đúng.

\(ABDC\) là hình bình hành \( \Leftrightarrow \)\(\overrightarrow {AC}  = \overrightarrow {BD} \) nên B đúng.

\(\overrightarrow {DB}  - \overrightarrow {DC}  = \overrightarrow {CB} \), điều này luôn đúng cho mọi điểm \(B,C,D\) nên điều kiện này không đủ để kết luận \(ABDC\) là hình bình hành nên C sai.

\(ABDC\) là hình bình hành \( \Leftrightarrow \)\(AD\) cắt \(BC\) tại trung điểm \(O\) của mỗi đường hay \(\overrightarrow {OA}  + \overrightarrow {OD}  = \overrightarrow 0 \), \(O\) là trung điểm của \(BC\) nên D đúng.

Chọn C.

Loigiaihay.com