Bài 1.71 trang 46 SBT hình học 10

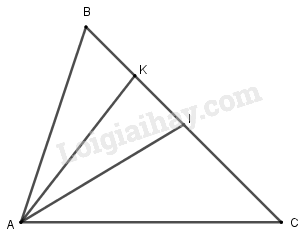
Đề bài

Cho tam giác \(ABC\). Gọi \(I\) là trung điểm của \(BC\), \(K\) là trung điểm của \(BI\).

Chứng minh rằng:

a) \(\overrightarrow {AK}  = \dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {AI} \);

b) \(\overrightarrow {AK}  = \dfrac{3}{4}\overrightarrow {AB}  + \dfrac{1}{4}\overrightarrow {AC} \).

Lời giải chi tiết

a) Vì \(K\) là trung điểm của \(BI\) nên \(\overrightarrow {AB}  + \overrightarrow {AI}  = 2\overrightarrow {AK} \)  \( \Leftrightarrow \overrightarrow {AK}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AI} } \right)\)(1)

b) Vì \(I\) là trung điểm của \(BC\) nên \(\overrightarrow {AI}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\)(2)

Thay (2) vào (1) ta được:

\(\overrightarrow {AK}  = \dfrac{1}{2}\left[ {\overrightarrow {AB}  + \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)} \right]\)\( = \dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{4}\overrightarrow {AB}  + \dfrac{1}{4}\overrightarrow {AC} \) \( = \dfrac{3}{4}\overrightarrow {AB}  + \dfrac{1}{4}\overrightarrow {AC} \)

Vậy \(\overrightarrow {AK}  = \dfrac{3}{4}\overrightarrow {AB}  + \dfrac{1}{4}\overrightarrow {AC} \).

Loigiaihay.com