Bài 16 trang 64 SBT toán 9 tập 1

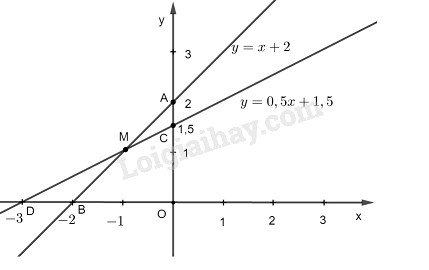
LG a

Xác định giá trị của $a$ để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng $2.$

Phương pháp giải:

Điểm $M({x_0};{y_0})$ thuộc đồ thị $y = ax + b$ khi ${y_0} = a{x_0} + b$

Lời giải chi tiết:

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng $y = 2,$ suy ra điểm đó có hoành độ $x=0$.

Thay $x=0$, $y=2$ vào hàm số $y = \left( {a - 1} \right)x + a\,\,\,\,\left( {a \ne 1} \right)$ ta được:

$2 = \left( {a - 1} \right).0+ a \Rightarrow a=2$ (thỏa mãn)

Vậy $a=2$.

Cách khác: 

Hàm số $y = \left( {a - 1} \right)x + a\,\,\,\,\left( {a \ne 1} \right)$ là hàm số bậc nhất có đồ thị hàm số cắt trục tung tại điểm có tung độ bằng $y = 2$ nên $a = 2.$

LG b

Xác định giá trị của $a$ để đồ thị hàm số cắt trục tung tại điểm có hoành độ bằng $-3.$

Phương pháp giải:

Điểm $M({x_0};{y_0})$ thuộc đồ thị $y = ax + b$ khi ${y_0} = a{x_0} + b$

Lời giải chi tiết:

Hàm số $y = \left( {a - 1} \right)x + a\,\,\,\,\left( {a \ne 1} \right)$ là hàm số bậc nhất có đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = -3$ nên tung độ giao điểm này bằng 0.

Ta có: 

$\eqalign{ & 0 = \left( {a - 1} \right)\left( { - 3} \right) + a \cr  & \Leftrightarrow - 3a + 3 + a = 0 \cr  & \Leftrightarrow - 2a = - 3 \Leftrightarrow a = 1,5 \cr}$

LG c

Vẽ đồ thị của hai hàm số ứng với giá trị của a tìm được ở các câu a) , b) trên cùng hệ  trục tọa độ $Oxy$ và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.

Phương pháp giải:

Cách vẽ đồ thị hàm số $y = ax + b$ $(a \ne 0)$

+ Nếu $b = 0$  ta có hàm số $y = ax$ . Đồ thị của  $y = ax$  là đường thẳng đi qua gốc tọa độ $O(0;0)$ và điểm $A(1;a)$;

+ Nếu $b \ne 0$ thì đồ thị $y = ax + b$ là đường thẳng đi qua các điểm $A(0;b)$; $B( - \dfrac{b}{a};0)$.

Lời giải chi tiết:

Khi $a = 2$ thì ta có hàm số: $y = x + 2$

Khi $a = 1,5$ thì ta có hàm số: $y = 0,5x + 1,5$

* Vẽ đồ thị của hàm số $y = x + 2$

Cho $x = 0$ thì $y = 2.$ Ta có: $A(0;2)$

Cho $y = 0$ thì $x = -2.$ Ta có: $B(-2;0)$

Đường thẳng AB là đồ thị hàm số $y = x + 2$.

* Vẽ đồ thị của hàm số $y = 0,5x + 1,5$

Cho $x = 0$ thì $y = 1,5.$ Ta có: $C(0;1,5)$

Cho $y = 0$ thì $x = -3.$ Ta có : $D(-3;0)$

Đường thẳng $CD$ là đồ thị hàm số $y = 0,5x + 1,5$

* Tọa độ giao điểm của hai đường thẳng .

Gọi $M(x_1;y_1)$ là giao điểm của hai đường thẳng $y = x + 2$ và $y = 0,5x + 1,5$. 

Ta có:

$M(x_1;y_1)$ thuộc đường thẳng $y = x + 2$ nên ${y_1} = {x_1} + 2$

$M(x_1;y_1)$ thuộc đường thẳng $y = 0,5x + 1,5$ nên ${y_1} = 0,5{x_1} + 1,5$

Suy ra:

$\eqalign{ & {x_1} + 2 = 0,5{x_1} + 1,5 \cr  & \Leftrightarrow 0,5{x_1} = - 0,5 \cr  & \Leftrightarrow {x_1} = - 1 \cr}$

${x_1} =  - 1 \Rightarrow {y_1} =  - 1 + 2 = 1$           

Vậy tọa độ giao điểm của hai đường thẳng là $M(-1;1).$ 

Loigiaihay.com