Bài 15 trang 71 Vở bài tập toán 7 tập 2

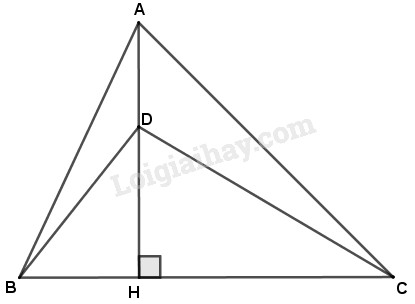
Đề bài

Cho tam giác \(ABC\) có \(AC > AB\). Kẻ đường vuông góc \(AH\) từ \(A\) đến đường thẳng \(BC\). Gọi \(D\) là điểm nằm giữa \(A\) và \(H\) (h.18).

a) So sánh độ dài các đoạn thẳng \(HC\) và \(HB\).

b) So sánh độ dài các đoạn thẳng \(DC\) và \(DB\).

Lời giải chi tiết

GT: \(\Delta ABC,AC > AB,AH \bot BC,D \in AH\)

KL: a) So sánh \(HC,HB\) 

       b) So sánh \(DC,DB\)

a) \(HC\) và \(HB\) lần lượt là hình chiếu của \(AC\) và \(AB\) kẻ từ \(A\) đến \(BC\).

Vì \(AC>AB\) nên \(HC>HB\) (đường xiên lớn hơn thì hình chiếu lớn hơn). 

b) \(HC\) và \(HB\) cũng lần lượt là hình chiếu của \(DC\), \(DB\) kẻ từ \(D\) đến đường thẳng \(BC\).

Vì \(HC>HB\) (theo câu a) nên \(DC>DB\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).

Loigiaihay.com