Bài 11 trang 69 Vở bài tập toán 7 tập 2

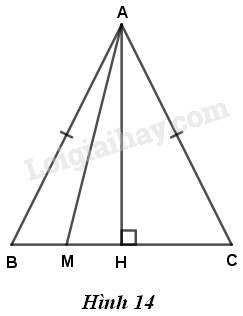
Đề bài

Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kỳ của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên.

Lời giải chi tiết

GT: \(\Delta ABC,AB = AC,AH \bot BC,M \in BC\)

KL: \(AM < AB\) hoặc \(AM = AB\)  

Gọi \(H\) là chân đường cao kẻ từ \(A\) đến đường thẳng \(BC\). Khi đó, \(BH,\,MH\) lần lượt là hình chiếu của \(AB\) và \(AM\) trên đường thẳng \(BC\).

- Nếu \(M  ≡ B\) (hoặc \(M  ≡  C\)) thì \(AM = AB\) hoặc \( AM = AC\).

- Nếu \(M ≡ H\) thì \(AM=AH<AB\) vì đường vuông góc ngắn hơn đường xiên.

- Nếu \(M\) nằm giữa \(B\) và \(H\) (hoặc \(M\) nằm giữa \(C\) và \(H\)) thì \(MH<BH\) (hoặc \(MH<CH\)). Theo định lí đường xiên và hình chiếu suy ra \(AM<AB\) (hoặc \(AM<AC\)).

Lưu ý: Cần chuyển bài toán được nêu dưới dạng tổng quát thành một bài toán cụ thể.

Loigiaihay.com