Bài 1.10 phần bài tập bổ sung trang 106 SBT toán 9 tập 1

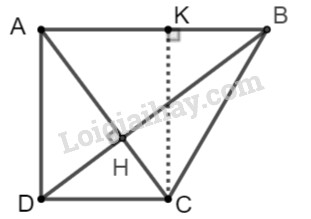
Đề bài

Cho hình thang \(ABCD\) vuông tại \(A\) có cạnh đáy \(AB\) bằng \(6cm\), cạnh bên \(AD\) bằng \(4cm\) và hai đường chéo vuông góc với nhau. Tính độ dài các cạnh \(DC, CB\) và đường chéo \(DB\).  

Lời giải chi tiết

Hai đường chéo \(AC, BD\) cắt nhau tại \(H\). Trong tam giác vuông \(ABD\), ta có: 

\(\dfrac{{HD}}{{HB}} =\dfrac{{HD.BD}}{{HB.BD}} = \dfrac{{A{D^2}}}{{A{B^2}}} \)\(= \dfrac{{{4^2}}}{{{6^2}}} = \dfrac{4}{9}.\) 

Ta có \(∆HDC \backsim ∆HBA\) (do \(\widehat {DHC} = \widehat {AHB} = {90^0};\,\widehat {ACD} = \widehat {CAB}\) (so le trong)) nên  

\(\dfrac{{DC}}{{AB}} = \dfrac{{HD}}{{HB}} = \dfrac{4}{9}\) 

Suy ra \(DC =\dfrac{4}{9}.AB= \dfrac{4}{9}.6 = \dfrac{8 }{3}\left( {cm} \right)\)

Kẻ đường cao \(CK\) của tam giác \(ABC\), suy ra \(ADCK\) là hình chữ nhật (vì có ba góc vuông) nên \(DC=KA;AD=KC\) (tính chất)

Suy ra \(KB = AB-KA=AB-DC\)\( = 6 - \dfrac{8}{3} = \dfrac{{10}}{3}.\)

Từ đó theo định lý Pytago cho tam giác vuông \(KBC\) ta có:

\(B{C^2} = K{B^2} + K{C^2} = K{B^2} + A{D^2}\)\( = \dfrac{{100}}{ 9} + 16 = \dfrac{{244}}{9}\) suy ra \(BC = \dfrac{{\sqrt {244} }}{3} = \dfrac{{2\sqrt {61} }}{3}\left( {cm} \right)\)

Tam giác vuông \(ABD,\) theo định lý Pytago ta có: \(D{B^2} = A{B^2} + A{D^2} \)\(= {6^2} + {4^2} = 52\), từ đó \(DB = \sqrt {52}  = 2\sqrt {13} \left( {cm} \right)\)

Loigiaihay.com