Bài 1.1, 1.2, 1.3, 1.4 trang 6, 7 SBT toán 7 tập 1

Bài 1.1

Tập hợp các phân số bằng phân số \(\displaystyle - {{25} \over {35}}\) là: 

(A) \(\displaystyle \left\{ { - {{25k} \over {35k}}|k \in\mathbb Z,k \ne 0} \right\};\)

(B) \(\displaystyle \left\{ { - {{2k} \over {3k}}|k \in\mathbb Z,k \ne 0} \right\};\)

(C) \(\displaystyle \left\{ { - {{50k} \over {70k}}|k \in\mathbb Z,k \ne 0} \right\};\) 

(D) \(\displaystyle \left\{ { - {{5k} \over {7k}}|k \in \mathbb Z,k \ne 0} \right\}\) 

Phương pháp giải:

Tập hợp các phân số bằng phân số \(\dfrac{a}{b}\) (trong đó \(\dfrac{a}{b}\) là phân số tối giản) là: 

\(\left\{ {\dfrac{{ak}}{{bk}}|k \in\mathbb Z ,\,k \ne 0} \right\}\). 

Lời giải chi tiết:

Ta có: \( - \dfrac{{25}}{{35}} =  - \dfrac{{5.5}}{{7.5}} =  - \dfrac{5}{7}\).

Tập hợp các phân số bằng phân số \(\displaystyle - {{25} \over {35}}\) là: 

\(\displaystyle \left\{ { - {{5k} \over {7k}}|k \in \mathbb Z,k \ne 0} \right\}\)

Chọn (D). 

Bài 1.2

Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng:

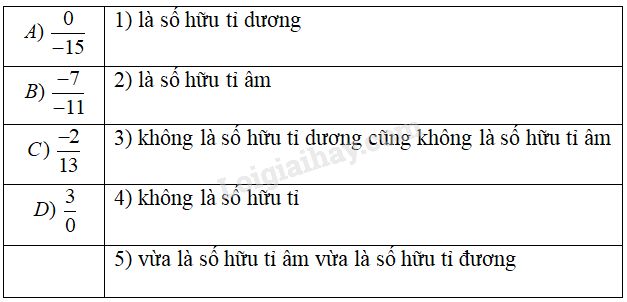
Phương pháp giải:

- Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b ∈ \mathbb Z, b \ne 0\) và được kí hiệu là \(\mathbb Q\).

- Số hữu tỉ lớn hơn \(0\) gọi là số hữu tỉ dương.

- Số hữu tỉ nhỏ hơn \(0\) gọi là số hữu tỉ âm.

- Số \(0\) không là số hữu tỉ dương, cũng không là số hữu tỉ âm.

Lời giải chi tiết:

\(\dfrac{0}{{ - 15}} = 0\) 

\(\dfrac{{ - 7}}{{ - 11}} = \dfrac{7}{{11}}\)

\(\dfrac{3}{0}\) không tồn tại theo định nghĩa số hữu tỉ.

Ta nối như sau: 

A nối với \(3\)

B nối với \(1\)

C nối với \(2\)

D nối với \(4\).

Bài 1.3

Viết dạng chung của các số hữu tỉ bằng \(\displaystyle{{ - 628628} \over {942942}}\) 

Phương pháp giải:

Dạng chung của các phân số bằng phân số \(\dfrac{a}{b}\) (trong đó \(\dfrac{a}{b}\) là phân số tối giản) là: 

\(\left\{ {\dfrac{{ak}}{{bk}}|k \in\mathbb Z ,\,k \ne 0} \right\}\).

Lời giải chi tiết:

Ta có: \(\displaystyle{{ - 628628} \over {942942}} = {{ - 2.314314} \over {3.314314}} =   {-2 \over 3}\)

Dạng chung của các số hữu tỉ bằng \(\displaystyle{{ - 628628} \over {942942}}\) là \(\displaystyle{{ - 2m} \over {3m}}\) (với \(m ∈\mathbb Z, m ≠ 0 \)).                   

Bài 1.4

Cho số hữu tỉ \(\displaystyle {a \over b}\) khác \(0\). Chứng minh rằng:

a) \(\displaystyle {a \over b}\) là số hữu tỉ dương nếu \(a\) và \(b\) cùng dấu.

b) \(\displaystyle {a \over b}\) là số hữu tỉ âm nếu \(a\) và \(b\) khác dấu. 

Phương pháp giải:

Hai phân số cùng mẫu dương, nếu tử phân số nào lớn hơn thì phân số đó lớn hơn.

Lời giải chi tiết:

Xét số hữu tỉ \(\displaystyle {a \over b}\), có thể coi \(b > 0\).

a) Nếu \(a, b\) cùng dấu thì \(a > 0\) và \(b > 0\).

Suy ra \(\displaystyle {a \over b} > {0 \over b} = 0\) tức là \(\displaystyle{a \over b}\) dương.

b) Nếu \(a, b\) khác dấu thì \(a < 0\) và \(b > 0\). 

Suy ra \(\displaystyle{a \over b} < {0 \over b} = 0\) tức là \(\displaystyle {a \over b}\) âm.

Loigiaihay.com