Bài 1 trang 60 SBT toán 9 tập 1Giải bài 1 trang 60 sách bài tập toán 9. Trong các bảng sau ghi các giá trị tương ứng của x và y. Bảng nào xác định y là hàm số của x? Vì sao?... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
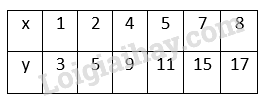
Trong các bảng sau ghi các giá trị tương ứng của \(x\) và \(y\). Bảng nào xác định \(y\) là hàm số của \(x\)? Vì sao? LG câu a Phương pháp giải: Sử dụng: Khái niệm về hàm số: Nếu đại lượng \(y\) phụ thuộc vào đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của \(x\). Kí hiệu \(y = f(x)\). Lời giải chi tiết: Xác định \(y\) là hàm số của biến số \(x\) vì với mỗi giá trị của \(x\) ta xác định được một giá trị tương ứng duy nhất của \(y.\) LG câu b
Phương pháp giải: Sử dụng: Khái niệm về hàm số: Nếu đại lượng \(y\) phụ thuộc vào đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của \(x\). Kí hiệu \(y = f(x)\). Lời giải chi tiết: Xác định \(y\) không phải là hàm số của biến số \(x\) vì với mỗi giá trị của \(x\) ta xác định được hai giá trị khác nhau của \(y.\) Ví dụ \(x = 3\) thì \(y = 6\) và \(y = 4\). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
