Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Đề bài
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\)có nghiệm là
Câu 2 :
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm\(M( - 2;6).\) Phương trình của (d) là
Câu 4 :
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Câu 5 :
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\)là
Câu 6 :
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm x0 = 1 thì m bằng:
Câu 7 :
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
Câu 8 :
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Câu 9 :
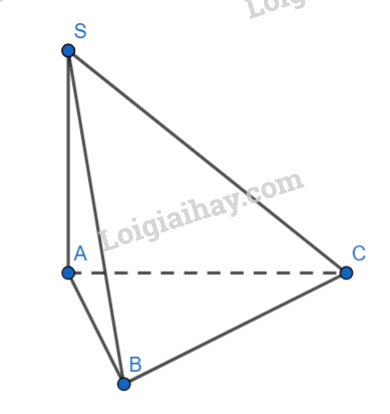
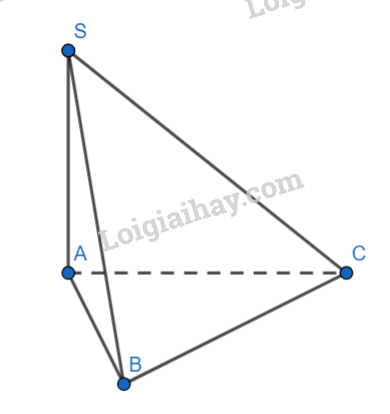
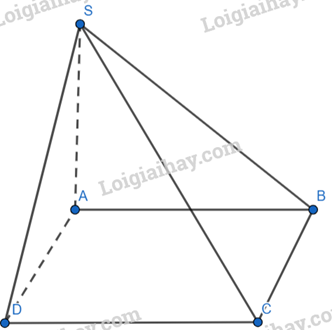
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Câu 10 :
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Câu 11 :
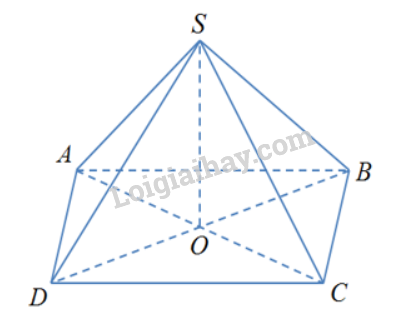
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
Câu 12 :
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\)bằng
Phần II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\).
Đúng
Sai
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\).
Đúng
Sai
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\).
Đúng
Sai
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\).
Đúng
Sai
a) Tứ phân vị thứ nhất \({Q_1}\) là 47
Đúng
Sai
b) Trung vị \({M_e}\) là 51,4
Đúng
Sai
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
Đúng
Sai
d) Mốt \({M_o} = 20\)
Đúng
Sai
Câu 3 :
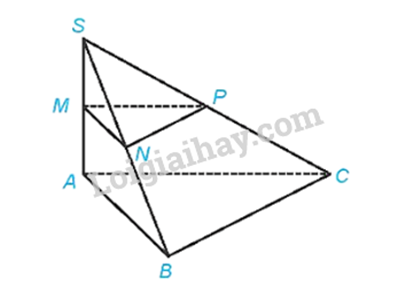
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. a) \(d((MNP),(ABC)) = h\)
Đúng
Sai
b) \(d(NP,(ABC)) = \frac{h}{2}\)
Đúng
Sai
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Đúng
Sai
d) \((MNP)//(ABC)\)
Đúng
Sai
Câu 4 :
Cho hàm số \(y = \sin x\) a) Đạo hàm của hàm số là \(y' = - cosx\)
Đúng
Sai
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
Đúng
Sai
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
Đúng
Sai
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Đúng
Sai
Phần III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6
Lời giải và đáp án
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\)có nghiệm là
Đáp án : C Phương pháp giải :
Sử dụng công thức đạo hàm. Lời giải chi tiết :
\(\begin{array}{l}f'(x) = \left( {\frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6} \right)' = 3{x^2} - 3x - 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 4\end{array} \right.\end{array}\) Đáp án C.
Câu 2 :
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm\(M( - 2;6).\) Phương trình của (d) là
Đáp án : C Phương pháp giải :
Phương trình tiếp tuyến với đồ thị (C): \(y = f(x) = - {x^3} + x\) tại điểm \(M({x_0};f({x_0})).\)là: \(y = f'(x{}_0)(x - x{}_0) + f(x{}_0)\) Trong đó: \(M({x_0};f({x_0}))\) gọi là tiếp điểm. \(k = f'(x{}_0)\)là hệ số góc. Lời giải chi tiết :
\(y' = f'(x) = \left( { - {x^3} + x} \right)' = - 3{x^2} + 1\) Phương trình tiếp tuyến của đồ thị \(y = f(x) = - {x^3} + x\)tại điểm \(M({x_0};f({x_0})).\) \(y' = f'( - 2)(x + 2) + 6 = - 11(x + 2) + 6 = - 11x - 16\) Đáp án C.
Đáp án : C Phương pháp giải :
Sử dụng công thức tính số trung bình của mẫu số liệu Lời giải chi tiết :
Trong mỗi khoảng thời gian, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:
Tổng số học sinh là n = 45. Thời gian trung bình giải bài toán của học sinh lớp 11 A là: \(\overline x = \frac{{6.9 + 17.12 + 17.15 + 5.18}}{{45}} = \frac{{67}}{5} = 13,4\) (phút) Đáp án C.
Câu 4 :
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Đáp án : A Phương pháp giải :
Áp dụng công thức tính đạo hàm. Lời giải chi tiết :
Ta có: \({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^2}}}\). \({\left( {k.u} \right)^\prime } = k.u'\). \({\left( {u + v} \right)^\prime } = u' + v'\). \(\left( {u.v} \right)' = u'.v + u.v'\). Vậy đáp án A sai.
Câu 5 :
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\)là
Đáp án : B Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm phân thức: \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\) Lời giải chi tiết :
\(y' = \left( {\frac{{2x - 1}}{{1 - x}}} \right)' = \left( {\frac{{2x - 1}}{{ - x + 1}}} \right)' = \frac{1}{{{{\left( { - x + 1} \right)}^2}}}\) Đáp án B.
Câu 6 :
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm x0 = 1 thì m bằng:
Đáp án : C Phương pháp giải :
Điều kiện để hàm số liên tục tại \(x = {x_0}\): \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\) Lời giải chi tiết :
Hàm số đã cho xác định trên R Ta có: \(\begin{array}{l}f(1) = m\\\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{1}{{x + 1}} = \frac{1}{2}\end{array}\) Hàm số liên tục tại \(x = 1\) khi \(f(1) = \mathop {\lim }\limits_{x \to 1} f(x) \Leftrightarrow m = \frac{1}{2}\) Vậy khi m = 2 thì hàm số liên tục tại \(x = 1\) Đáp án C.
Câu 7 :
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
Đáp án : D Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm hợp Lời giải chi tiết :
\(y' = 4{x^3} - 6x + 2\) Đáp án D.
Câu 8 :
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Đáp án : A Phương pháp giải :
Nhận dạng: \(\mathop {\lim }\limits_{x \to \infty } \frac{{f(x)}}{{g(x)}}\) TH1: Nếu f(x) , g(x) là các đa thức thì chia cả tử và mẫu cho lũy thừa cao nhất của x. TH2: Nếu f(x) , g(x) chứa căn thì có thể chia cả tử và mẫu cho lũy thừa cao nhất của x hoặc nhân lượng liên hợp Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to \infty } f(x) = \mathop {\lim }\limits_{x \to \infty } \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}} = \mathop {\lim }\limits_{x \to \infty } \frac{{{x^2}(a + \frac{4}{x} + \frac{3}{{{x^2}}})}}{{{x^2}( - 2a + \frac{3}{x})}} = \frac{a}{{ - 2a}} = \frac{{ - 1}}{2}\) Đáp án A.
Câu 9 :
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Đáp án : B Phương pháp giải :
Bước 1: Tìm giao điểm O của đường thẳng a và \((\alpha )\) Bước 2: Xác định hình chiếu A’ của điểm A xuống \((\alpha )\) Bước 3: Suy ra: \(\left( {AO,(\alpha )} \right) = \left( {AO,A'O} \right) = \widehat {AOA'}\) Lời giải chi tiết :
Do \(SA \bot (ABC)\)nên A là hình chiếu của S lên (ABC) Ta có: \(\left( {SB,(ABC)} \right) = (SB,AB)\) Xét \(\Delta SAB\) vuông tại A có: \(\begin{array}{l}\tan \left( {SB,AB} \right) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{\sqrt {S{B^2} - A{B^2}} }}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \\ \Rightarrow \widehat {SBA} = {60^0}\end{array}\) Đáp án B.
Câu 10 :
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Đáp án : B Phương pháp giải :
Sử dụng định lý đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc với nhau Lời giải chi tiết :
Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\\SA,AD \subset (SAD)\\SA \cap AD\end{array} \right. \Rightarrow CD \bot (SAD)\\CD \subset (SCD) \Rightarrow (SCD) \bot (SAD)\end{array}\) Đáp án B.
Câu 11 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
Đáp án : C Phương pháp giải :
Sử dụng định lý đường thẳng vuông góc với mặt phẳng Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}AC \bot BD\\AC \bot SO\\BD,SO \subset (SBD)\\BD \cap SO\end{array} \right. \Rightarrow AC \bot (SBD)\) Đáp án C.
Câu 12 :
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\)bằng
Đáp án : B Phương pháp giải :
Sử dụng phương tính đạo hàm của hàm hợp Lời giải chi tiết :
\(\begin{array}{l}g'\left( x \right) = \left[ {\frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}}} \right]' = \left( {\frac{{18{x^3} - 15{x^2} - 4x + 4}}{{x - 1}}} \right)'\\ = \frac{{\left( {18{x^3} - 15{x^2} - 4x + 4} \right)'(x - 1) - (18{x^3} - 15{x^2} - 4x + 4)(x - 1)'}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{36{x^3} - 69{x^2} + 30x}}{{{{\left( {x - 1} \right)}^2}}}\\g'\left( 2 \right) = 72\end{array}\) Đáp án B.
Phần II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\).
Đúng
Sai
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\).
Đúng
Sai
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\).
Đúng
Sai
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\).
Đúng
Sai
Đáp án
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\).
Đúng
Sai
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\).
Đúng
Sai
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\).
Đúng
Sai
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\).
Đúng
Sai
Phương pháp giải :
Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố. Lời giải chi tiết :
Không gian mẫu: \((\Omega ) = C_{20}^3 = 1140\). a) Đúng. Gọi A là biến cố: “3 viên bi lấy ra đều màu đỏ”. \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_8^3}}{{C_{20}^3}} = \frac{{56}}{{1140}} = \frac{{14}}{{285}}\). b) Đúng. B là biến cố: “3 viên bi lấy ra có không quá hai màu”. TH1: Số cách lấy ra 3 viên bi lấy ra chỉ có một màu: \(C_8^3 + C_7^3 + C_5^3 = 101\). TH2: Số cách lấy ra 3 viên bi lấy ra chỉ có đúng hai màu: \(\left[ {C_{15}^3 - \left( {C_8^3 + C_7^3} \right)} \right] + \left[ {C_{13}^3 - \left( {C_8^3 + C_5^3} \right)} \right] + \left[ {C_{12}^3 - \left( {C_5^3 + C_7^3} \right)} \right] = 759\). Do đó \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{101 + 759}}{{1140}} = \frac{{43}}{{57}}\). c) Sai. C là biến cố: “3 viên bi lấy ra đều có màu vàng”. \(P(C) = \frac{{n(C)}}{{n(\Omega )}} = \frac{{C_5^3}}{{C_{20}^3}} = \frac{{10}}{{1140}} = \frac{1}{{114}}\). d) Đúng. D là biến cố: “3 viên bi lấy ra có đủ cả ba màu”. \(P(D) = \frac{{n(D)}}{{n(\Omega )}} = \frac{{C_8^1.C_7^1.C_5^1}}{{C_{20}^3}} = \frac{{280}}{{1140}} = \frac{{14}}{{57}}\). a) Tứ phân vị thứ nhất \({Q_1}\) là 47
Đúng
Sai
b) Trung vị \({M_e}\) là 51,4
Đúng
Sai
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
Đúng
Sai
d) Mốt \({M_o} = 20\)
Đúng
Sai
Đáp án
a) Tứ phân vị thứ nhất \({Q_1}\) là 47
Đúng
Sai
b) Trung vị \({M_e}\) là 51,4
Đúng
Sai
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
Đúng
Sai
d) Mốt \({M_o} = 20\)
Đúng
Sai
Phương pháp giải :
Sử dụng công thức tính tứ phân vị của mẫu số liệu và Mốt Lời giải chi tiết :
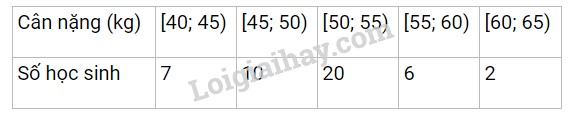
Cỡ mẫu là n = 7 + 10 + 20 + 6 + 2 = 45 Gọi x1, x2, ….., x45 là cân nặng của 45 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là x23. Do giá trị x23 thuộc nhóm [50; 55) nên nhóm này chứa trung vị. Do đó p = 3; a3 = 50, m3 = 20; m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5 Khi đó \({M_e} = {a_3} + \frac{{\frac{n}{2} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{45}}{2} - 17}}{{20}}.5 \approx 51,4\). Vậy Me = 51,4. Từ Me = 51,4, suy ra Q2 = 51,4. - Tứ phân vị thứ nhất Q1 là trung vị của nửa dãy bên trái Q2 nên \({Q_1} = \frac{{{x_{11}} + {x_{12}}}}{2}\) Do x11 và x12 đều thuộc nhóm [45; 50) nên nhóm này chứa Q1. Do đó, p = 2, a2 = 45, m2 = 10, m1 = 7; a3 – a2 = 5. Ta có \({Q_1} = {a_2} + \frac{{\frac{n}{4} - {m_1}}}{{{m_2}}}({a_3} - {a_2}) = 45 + \frac{{\frac{{45}}{2} - 7}}{{10}}.5 \approx 47,1\) - Tứ phân vị thứ ba Q3 là trung vị của nửa dãy bên phải Q2 nên \({Q_3} = \frac{{{x_{34}} + {x_{35}}}}{2}\). Do x34 và x35 đều thuộc nhóm [50; 55) nên nhóm này chứa Q3. Do đó, p = 3, a3 = 50, m3 = 20, m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5. Ta có \({Q_3} = {a_3} + \frac{{\frac{{3n}}{4} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{3.45}}{4} - 17}}{{20}}.5 \approx 54,2\) . Vậy tứ phân vị: Q1 ≈ 47,1; Q2 ≈ 51,4; Q3 ≈ 54,2. - Ta thấy tần số lớn nhất là 20 nên nhóm chứa mốt là nhóm [50; 55). Ta có j = 3, a3 = 50, m3 = 20, m2 = 10, m4 = 6, h = 55 – 50 = 5 Khi đó \({M_0} = {a_3} + \frac{{{m_3} - {m_2}}}{{\left( {{m_3} - {m_2}} \right) + \left( {{m_3} - {m_4}} \right)}}h = 50 + \frac{{20 - 10}}{{(20 - 10) + (20 - 6)}}.5 \approx 52,1\) Vậy Mo ≈ 52,1.
Câu 3 :
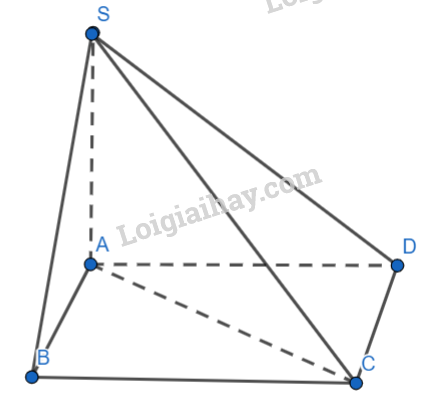
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. a) \(d((MNP),(ABC)) = h\)
Đúng
Sai
b) \(d(NP,(ABC)) = \frac{h}{2}\)
Đúng
Sai
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Đúng
Sai
d) \((MNP)//(ABC)\)
Đúng
Sai
Đáp án
a) \(d((MNP),(ABC)) = h\)
Đúng
Sai
b) \(d(NP,(ABC)) = \frac{h}{2}\)
Đúng
Sai
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Đúng
Sai
d) \((MNP)//(ABC)\)
Đúng
Sai
Phương pháp giải :
Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng và khoảng cách từ đường thẳng đến mặt phẳng Lời giải chi tiết :
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB. Suy ra \(MN//AB\),do đó \(MN//(ABC)\) Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC. Suy ra \(PN//BC\),do đó \(PN//(ABC)\) Khi đó, \(d((MNP),(ABC)) = d(M,(ABC))\) Vì \(SA \bot (ABC)\) nên \(MA \bot (ABC)\). Do đó \(d(M,(ABC)) = MA\) Vì M là trung điểm SA nên \(AM = \frac{{SA}}{2} = \frac{h}{2}\) Do đó \(d((MNP),(ABC)) = \frac{h}{2}\) b) Vì \(PN//(ABC)\) nên \(d(NP,(ABC)) = d(N,(ABC))\) Vì \(MN//(ABC)\) nên \(d(N,(ABC)) = d(M,(ABC)) = MA = \frac{h}{2}\) Vậy \(d(N,(ABC)) = \frac{h}{2}\) c) Vì tam giác ABC là tam giác vuông tại B nên \(BC \bot AB\) Vì \(SA \bot (ABC)\) nên \(SA \bot BC\)mà \(BC \bot AB\) nên \(BC \bot (SAB)\), suy ra \((SBC) \bot (SAB)\) Kẻ \(AH \bot SB\) tại H Vì \(\left\{ \begin{array}{l}(SBC) \bot (SAB)\\(SBC) \cap (SAB) = SB\\AH \subset (SAB)\\AH \bot SB\end{array} \right. \Rightarrow AH \bot (SBC)\) Khi đó \(d(A,(SBC)) = AH\)\(\) Vì \(SA \bot (SBC)\) nên \(SA \bot AB\) Xét tam giác SAB vuông tại A, AH là đường cao, có: \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{a^2}{h^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\) Vậy \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\) d)\(MN//(ABC)\) mà \(MN \subset (MNP) \Rightarrow (MNP)//(ABC)\)
Câu 4 :
Cho hàm số \(y = \sin x\) a) Đạo hàm của hàm số là \(y' = - cosx\)
Đúng
Sai
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
Đúng
Sai
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
Đúng
Sai
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Đúng
Sai
Đáp án
a) Đạo hàm của hàm số là \(y' = - cosx\)
Đúng
Sai
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
Đúng
Sai
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
Đúng
Sai
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Đúng
Sai
Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm số lượng giác Lời giải chi tiết :
a) \(y' = (\sin x)' = cosx\) b) \(y'(\frac{\pi }{2}) = \cos \frac{\pi }{2} = 0\) c) \(\begin{array}{l}y'' = \left( {cosx} \right)' = - \sin x\\y''\left( {\frac{\pi }{2}} \right) = - 1\end{array}\) d) \(\begin{array}{l}{y^{(n)}} = \sin (x + n\frac{\pi }{2})\\{y^{(2024)}} = \sin (x + 1012\pi )\end{array}\)
Phần III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6
Phương pháp giải :
Sử dụng phương pháp nhân liên hợp và phân tích thành nhân tử. Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {\sqrt {4x + 1} - 3} \right)\left( {\sqrt {4x + 1} + 3} \right)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{(4x + 1) - 9}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}}\) \( = \mathop {\lim }\limits_{x \to 2} \frac{{4x - 8}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{4(x - 2)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{4}{{\sqrt {4x + 1} + 3}} = \frac{4}{{\sqrt {4.2 + 1} + 3}} = \frac{2}{3}\). Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm hợp Lời giải chi tiết :
\(\begin{array}{l}y' = \left[ {{{\left( {{x^4} - 1} \right)}^4}} \right]' = 4.{\left( {{x^4} - 1} \right)^3}.4{x^3} = 16{x^3}{\left( {{x^4} - 1} \right)^3}\\y'(1) = 0\end{array}\) Phương pháp giải :
Bước 1: Tính \(f({x_0}) = {f_2}({x_0})\) Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\) Bước 3: Nếu \({f_2}({x_0}) = L\) thì hàm số f(x) liên tục tại \({x_0}\) Nếu \({f_2}({x_0}) \ne L\)thì hàm số f(x) không liên tục tại \({x_0}\). (Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m) Lời giải chi tiết :
Hàm số đã cho xác định trên R Ta có: \(f(1) = 1 - m\) \(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x - 2)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x - 2) = - 1\) Để hàm số liên tục tại x = 1 khi \(f(1) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} \Leftrightarrow 1 - m = - 1 \Leftrightarrow m = 2\) Phương pháp giải :
Sử dụng phương pháp tính góc giữa hai mặt phẳng Lời giải chi tiết :
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\,\\BC \bot SA\,\,(Do\,\,SA \bot (ABCD))\\AB,SA \subset (SAB)\\AB \cap SA\end{array} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow BC \bot SB\end{array}\)\(SA \bot (ABCD) \Rightarrow SA \bot AB\) Ta có: \(\left\{ \begin{array}{l}(SBC) \cap (ABCD) = BC\\SB \subset (SBC),SB \bot BC\\AB \subset (ABCD),AB \bot BC\end{array} \right. \Rightarrow \left( {(SBC),(ABCD)} \right) = (SB,AB)\) Do \(SA \bot (ABCD) \Rightarrow SA \bot AB\). Xét tam giác SAB vuông tại A có: \(\tan (SB,AB) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 \) Phương pháp giải :
Lập biểu thức tính khoảng cách từ điểm \(I( - 1;2)\) tới tiếp tuyển của đồ thị. Sử dụng BĐT Cauchy để tìm giá trị lớn nhất của biểu thức. Lời giải chi tiết :
Gọi đồ thị của hàm số là (C). Ta có \(y = \frac{{2x - 1}}{{x + 1}} = 2 - \frac{3}{{x + 1}}\); \(y' = \frac{3}{{{{(x + 1)}^2}}}\). Giả sử \(M\left( {{x_0};2 - \frac{3}{{{x_0} + 1}}} \right) \in (C)\). PTTT của (C) tại M là: \(\left( \Delta \right)\): \(y = \frac{3}{{{{({x_0} + 1)}^2}}}(x - {x_0}) + 2 - \frac{3}{{{x_0} + 1}}\) \( \Leftrightarrow \frac{3}{{{{({x_0} + 1)}^2}}}x - y + \left[ { - \frac{{3{x_0}}}{{{{({x_0} + 1)}^2}}} + 2 - \frac{3}{{{x_0} + 1}}} \right] = 0\) \( \Leftrightarrow \frac{3}{{{{({x_0} + 1)}^2}}}x - y + \left[ { - \frac{{3{x_0}}}{{{{({x_0} + 1)}^2}}} + 2 - \frac{{3{x_0} + 3}}{{{{({x_0} + 1)}^2}}}} \right] = 0\) \( \Leftrightarrow \frac{3}{{{{({x_0} + 1)}^2}}}x - y + 2 - \frac{{6{x_0} + 3}}{{{{({x_0} + 1)}^2}}} = 0\). Ta có \(d(I,\Delta ) = \frac{{\left| {\frac{3}{{{{({x_0} + 1)}^2}}}.( - 1) - 2 + 2 - \frac{{6{x_0} + 3}}{{{{({x_0} + 1)}^2}}}} \right|}}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^4}}} + 1} }}\) \( = \frac{{\left| {\frac{{ - 6{x_0} - 6}}{{{{({x_0} + 1)}^2}}}} \right|}}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^4}}} + 1} }} = \frac{{\frac{{6\left| {{x_0} + 1} \right|}}{{{{({x_0} + 1)}^2}}}}}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^4}}} + 1} }} = \frac{{6\left| {{x_0} + 1} \right|}}{{\sqrt {9 + {{({x_0} + 1)}^4}} }} = \frac{6}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^2}}} + {{({x_0} + 1)}^2}} }}\). Áp dụng BĐT Cauchy: \(\frac{9}{{{{({x_0} + 1)}^2}}} + {({x_0} + 1)^2} \ge 2\sqrt 9 = 6 \Rightarrow d \le \sqrt 6 \). Dấu “=” xảy ra khi \(\frac{9}{{{{({x_0} + 1)}^2}}} = {({x_0} + 1)^2} \Leftrightarrow {x_0} = - 1 \pm \sqrt 3 \). Vậy có hai điểm cần tìm là \(M( - 1 + \sqrt 3 ;2 - \sqrt 3 )\) hoặc \(M( - 1 - \sqrt 3 ;2 + \sqrt 3 )\). Phương pháp giải :
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(M{(1 + r\% )^{k - 1}},k \in N*\) Trong đó: M: là lượng thứ ăn trang trại ăn hết trong mỗi ngày r (%): là % mức tiêu thụ thức ăn tăng thêm mỗi ngày Lời giải chi tiết :
Theo dự định, mỗi ngày, trang trại ăn hết: \(1:50 = \frac{1}{{50}}\)(lượng thức ăn) Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(\frac{1}{{50}}{(1 + 3\% )^{k - 1}},k \in N*\) Xác định số tự nhiên n nhỏ nhât để: \(\begin{array}{l}\frac{1}{{50}} + \frac{1}{{50}}(1 + 3\% ) + \frac{1}{{50}}{(1 + 3\% )^2} + ... + \frac{1}{{50}}{(1 + 3\% )^{n - 1}} \ge 1\\ \Leftrightarrow \frac{1}{{50}}(1 + 1,03 + 1,{03^2} + ... + 1,{03^{n - 1}}) \ge 1\\ \Leftrightarrow \frac{1}{{50}}.\frac{{1,{{03}^{n - 1}} - 1}}{{1,03 - 1}} \ge 1 \Leftrightarrow 1,{03^{n - 1}} - 1 \ge 1,5 \Leftrightarrow 1,{03^{n - 1}} \ge 2,5 \Leftrightarrow n - 1 \ge {\log _{1,03}}2,5 \Leftrightarrow n \ge 31,99 \Rightarrow {n_{Min}} = 32\end{array}\)
|


























Danh sách bình luận