Đề thi, đề kiểm tra Toán lớp 11 - Cánh diều

Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 1

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Làm đề thi

Câu 1: Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?

Đề bài

I. Trắc nghiệm
Câu 1 :

Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?

  • A
    \({\left( {{a^m}} \right)^n} = {a^{m + n}}\).
  • B
    \({\left( {{a^m}} \right)^n} = {a^{m - n}}\).
  • C
    \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).
  • D
    \({\left( {{a^m}} \right)^n} = {a^{\frac{m}{n}}}\).
Câu 2 :

Chọn đáp án đúng.

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:

  • A
    \({a^{ - n}} = \frac{1}{{{a^n}}}\).
  • B
    \({a^{1 - n}} = \frac{1}{{{a^n}}}\).
  • C
    \({a^{\frac{1}{n}}} = \frac{1}{{{a^n}}}\).
  • D
    Cả A, B, C đều sai.
Câu 3 :

Chọn đáp án đúng:

  • A
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[6]{{ab}}\).
  • B
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[9]{{ab}}\).
  • C
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{a + b}}\).
  • D
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).
Câu 4 :

Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).

  • A
    \({a^2}\).
  • B
    a.
  • C
    \(\frac{1}{a}\).
  • D
    \(2{a^2}\).
Câu 5 :

Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?

  • A
    \(a = \frac{3}{4}\).
  • B
    \(a = \frac{1}{2}\).
  • C
    \(a = 1\).
  • D
    \(a = \frac{3}{2}\).
Câu 6 :

Chọn đáp án đúng.

\({\log _a}b\) xác định khi và chỉ khi:

  • A
    \(a > 0\).
  • B
    \(a > 1\).
  • C
    \(a > 0,a \ne 1,b > 0\).
  • D
    \(a > 1,b > 0\).
Câu 7 :

Chọn đáp án đúng.

  • A
    \({\log _{1000}}{1000^3} = {1000^3}\).
  • B
    \({\log _{1000}}{1000^3} = \frac{1}{3}\).
  • C
    \({\log _{1000}}{1000^3} = 3\).
  • D
    \({\log _{1000}}{1000^3} = {3^{1000}}\).
Câu 8 :

Khẳng định nào sau đây đúng?

  • A
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
  • B
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).
  • C
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
  • D
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\ln a\).
Câu 9 :

Giá trị của phép tính \({4^{{{\log }_{\sqrt 2 }}3}}\) là:

  • A
    81.
  • B
    \(9\).
  • C
    \(\frac{1}{{81}}\).
  • D
    \(\frac{1}{9}\).
Câu 10 :

Chọn đáp án đúng:

  • A
    \({\log _5}15 - 2{\log _5}\sqrt 3  =  - 1\).
  • B
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 1\).
  • C
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 0\).
  • D
    \({\log _5}15 - 2{\log _5}\sqrt 3  = \frac{1}{2}\).
Câu 11 :

Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng:

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    3.
Câu 12 :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là:

  • A
    \(D = \left( {0; + \infty } \right)\).
  • B
    \(D = \left( { - \infty ;0} \right)\).
  • C
    \(D = \left( { - \infty ; + \infty } \right)\).
  • D
    Cả A, B, C đều sai.
Câu 13 :

Hàm số \(y = {\log _2}x\) đồng biến trên khoảng nào sau đây?

  • A
    \(\left( { - 1; + \infty } \right)\).
  • B
    \(\left[ {0; + \infty } \right)\).
  • C
    \(\left[ { - 1; + \infty } \right)\).
  • D
    \(\left( {1; + \infty } \right)\).
Câu 14 :

Hàm số nào dưới đây là hàm số mũ?

  • A
    \(y = {x^{\sqrt 2 }}\).
  • B
    \(y = {x^{\log 4}}\).
  • C
    \(y = {\left( {\frac{\pi }{2}} \right)^x}\).
  • D
    \(y = {\log _2}x\).
Câu 15 :

Hàm số nào dưới đây có đồ thị như hình dưới?

  • A
    \(y = {3^x}\).
  • B
    \(y = {\left( {\frac{1}{2}} \right)^x}\).
  • C
    \(y = {\left( {\frac{1}{3}} \right)^x}\).
  • D
    \(y = {\left( {\sqrt 2 } \right)^x}\).
Câu 16 :

Cho hàm số \(f\left( x \right) = {2^x}\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - 2;3} \right]\). Khi đó:

  • A
    \(M.m = 2\).
  • B
    \(M.m = \frac{1}{2}\)
  • C
    \(M.m = 4\).
  • D
    \(M.m = \frac{1}{4}\).
Câu 17 :

Cho hai biến cố A và B, biến cố hợp của hai biến cố A và B kí hiệu là:

  • A
    \(A \cup B\).
  • B
    \(A \cap B\).
  • C
    AB.
  • D
    \(A + B\).
Câu 18 :

Trong mẫu số liệu ghép nhóm, tứ phân vị thứ hai \({Q_2}\) bằng:

  • A
    Số trung bình cộng.
  • B
    Mốt.
  • C
    Trung vị.
  • D
    Cả A, B, C đều sai.
Câu 19 :

Kết quả kiểm tra môn Toán của lớp 11E được cho ở bảng tần số ghép nhóm sau:

Nhóm nào có tần số bằng 12?

  • A
    \(\left[ {3;5} \right)\).
  • B
    \(\left[ {5;7} \right)\).
  • C
    \(\left[ {7;9} \right)\).
  • D
    \(\left[ {9;11} \right)\).
Câu 20 :

Cho hai biến cố A và B. A và B gọi là hai biến cố xung khắc khi:

  • A
    \(A \cap B = \emptyset \).
  • B
    \(A \cap B = A\).
  • C
    \(A \cap B = B\).
  • D
    \(A \cup B = A\).
Câu 21 :

Hai bạn Hạnh và Hà cùng chơi trò chơi bắn cung một cách độc lập. Mỗi bạn chỉ bắn một lần. Xác suất để Hạnh và Hà bắn trúng bia lần lượt là 0,6 và 0,7 trong lần bắn của mình. Xác suất của biến cố: “Bạn Hạnh và bạn Hà đều bắn trượt bia” là:

  • A
    0,4.
  • B
    0,42.
  • C
    0,7
  • D
    0,12.
Câu 22 :

Một hộp chứa 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; ...; 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ rút ra là số chia hết cho 3” và biến cố B “Số xuất hiện trên thẻ rút ra là số chia hết cho 4”. Chọn đáp án đúng.

  • A
    \(A \cap B = \left\{ {3;6;9;12;...;48;51} \right\}\).
  • B
    \(A \cap B = \left\{ {4;8;12;16;...;48;52} \right\}\).
  • C
    \(A \cap B = \left\{ {12;24;36;48} \right\}\).
  • D
    Cả A, B, C đều sai.
Câu 23 :

Sau khi điều tra về số học sinh trong 100 lớp học, người ta chia mẫu số liệu đó thành năm nhóm căn cứ vào số lượng học sinh của mỗi lớp (đơn vị: học sinh) và lập bảng tần số ghép nhóm như bảng sau:

Trung vị của mẫu số liệu thuộc là: (làm tròn kết quả đến hàng đơn vị)

  • A
    43.
  • B
    41.
  • C
    42.
  • D
    40.
Câu 24 :

Góc giữa hai đường thẳng a và b có thể bằng:

  • A
    1800.
  • B
    1500.
  • C
    900.
  • D
    Cả A, B, C đều sai.
Câu 25 :

Trong không gian cho hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đúng?

  • A
    a và b cắt nhau.
  • B
    a và b chéo nhau.
  • C
    a và b cùng nằm trên một mặt phẳng.
  • D
    Góc giữa a và b bằng \({90^0}\).
Câu 26 :

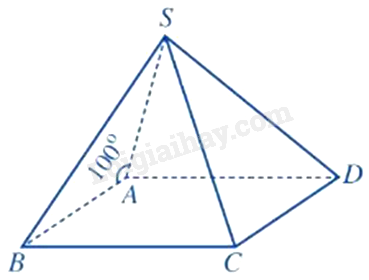
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = {100^0}\). Góc giữa hai đường thẳng SA và CD bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).
Câu 27 :

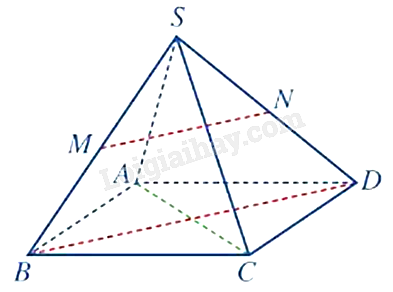
Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Khi đó, góc giữa hai đường thẳng AC và MN bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).
Câu 28 :

Có bao nhiêu mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước?

  • A
    Vô số.
  • B
    1.
  • C
    2.
  • D
    3.
Câu 29 :

Chọn đáp án đúng:

  • A
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
  • B
    Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
  • C
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
  • D
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
Câu 30 :

Chọn đáp án đúng.

  • A
    Có hai đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • B
    Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • C
    Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • D
    Có ba đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Câu 31 :

Cho đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P. Góc giữa hai đường thẳng d và d’ bằng bao nhiêu độ?

  • A
    \({30^0}\).
  • B
    \({45^0}\).
  • C
    \({60^0}\).
  • D
    \({90^0}\).
Câu 32 :

Cho hình chóp S. ABCD có ABCD là hình chữ nhật, SA vuông góc với đáy. Đường thẳng BC vuông góc với mặt phẳng nào?

  • A
    (SAD).
  • B
    (SCD).
  • C
    (SAC).
  • D
    (SAB).
Câu 33 :

Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúng.

  • A
    \(BC \bot AB\).
  • B
    \(BC \bot AH\).
  • C
    \(BC \bot SC\).
  • D
    Cả A, B, C đều sai.
Câu 34 :

Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’A và D’B’ bằng:

  • A
    \({30^0}\).
  • B
    \({60^0}\).
  • C
    \({90^0}\).
  • D
    \({45^0}\).
Câu 35 :

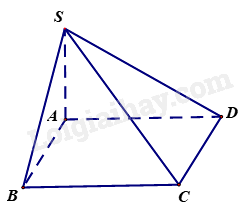
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\). Chọn đáp án đúng.

  • A
    \(\left( {AB,SD} \right) = {90^0}\).
  • B
    \(\left( {AB,SD} \right) = {85^0}\).
  • C
    \(\left( {AB,SD} \right) = {70^0}\).
  • D
    \(\left( {AB,SD} \right) = {75^0}\).
II. Tự luận
Câu 1 :

Cho hàm số: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\).

a) Với \(m = \frac{1}{3}\), hãy tìm tập xác định của hàm số trên.

b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định là \(\mathbb{R}\).
Câu 2 :

Cho hình chóp S. ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC và SD. Chứng minh rằng:

a) \(SC \bot \left( {AHK} \right)\).

b) \(HK \bot \left( {SAC} \right)\) và \(HK \bot AI\).
Câu 3 :

So sánh các số sau: \(A = \frac{1}{{1000}};B = {\left( {\frac{{99}}{{1000}}} \right)^3};C = {\left( {\frac{1}{{{{11}^2}}} + \frac{1}{{{{12}^2}}} + ... + \frac{1}{{{{1000}^2}}}} \right)^3}\).

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?

  • A
    \({\left( {{a^m}} \right)^n} = {a^{m + n}}\).
  • B
    \({\left( {{a^m}} \right)^n} = {a^{m - n}}\).
  • C
    \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).
  • D
    \({\left( {{a^m}} \right)^n} = {a^{\frac{m}{n}}}\).

Đáp án : C

Phương pháp giải :

Với a là số thực dương và m, n là hai số thực tùy ý thì \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).

Lời giải chi tiết :

Với a là số thực dương và m, n là hai số thực tùy ý thì \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).

Câu 2 :

Chọn đáp án đúng.

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:

  • A
    \({a^{ - n}} = \frac{1}{{{a^n}}}\).
  • B
    \({a^{1 - n}} = \frac{1}{{{a^n}}}\).
  • C
    \({a^{\frac{1}{n}}} = \frac{1}{{{a^n}}}\).
  • D
    Cả A, B, C đều sai.

Đáp án : A

Phương pháp giải :

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì \({a^{ - n}} = \frac{1}{{{a^n}}}\).

Lời giải chi tiết :

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì \({a^{ - n}} = \frac{1}{{{a^n}}}\).

Câu 3 :

Chọn đáp án đúng:

  • A
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[6]{{ab}}\).
  • B
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[9]{{ab}}\).
  • C
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{a + b}}\).
  • D
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).

Đáp án : D

Phương pháp giải :

\(\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\) (với các biểu thức đều có nghĩa).

Lời giải chi tiết :

Ta có: \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).

Câu 4 :

Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).

  • A
    \({a^2}\).
  • B
    a.
  • C
    \(\frac{1}{a}\).
  • D
    \(2{a^2}\).

Đáp án : B

Phương pháp giải :

\({a^m}.{a^n} = {a^{m + n}};{\left( {{a^m}} \right)^n} = {a^{mn}},{a^m}:{a^n} = {a^{m - n}}\) (a khác 0).

Lời giải chi tiết :

\(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}} = \frac{{{a^{\sqrt 5  + 1 + 7 - \sqrt 5 }}}}{{{a^{\left( {3 + \sqrt 2 } \right)\left( {3 - \sqrt 2 } \right)}}}} = \frac{{{a^8}}}{{{a^7}}} = a\)

Câu 5 :

Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?

  • A
    \(a = \frac{3}{4}\).
  • B
    \(a = \frac{1}{2}\).
  • C
    \(a = 1\).
  • D
    \(a = \frac{3}{2}\).

Đáp án : D

Phương pháp giải :

Nếu \(a > 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha  > \beta \)

Nếu \(0 < a < 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha  < \beta \)

Lời giải chi tiết :

Ta có: \(\frac{1}{{{a^{ - 3}}}} = {a^3} = {a^{\sqrt 9 }}\) nên \({a^{\sqrt 8 }} < {a^{\sqrt 9 }}\)

Vì \(\sqrt 8  < \sqrt 9 \), mà \({a^{\sqrt 8 }} < {a^{\sqrt 9 }}\) nên \(a > 1\). Do đó, \(a = \frac{3}{2}\) thỏa mãn yêu cầu bài toán.

Câu 6 :

Chọn đáp án đúng.

\({\log _a}b\) xác định khi và chỉ khi:

  • A
    \(a > 0\).
  • B
    \(a > 1\).
  • C
    \(a > 0,a \ne 1,b > 0\).
  • D
    \(a > 1,b > 0\).

Đáp án : C

Phương pháp giải :

\({\log _a}b\) xác định khi và chỉ khi \(a > 0,a \ne 1,b > 0\).

Lời giải chi tiết :

\({\log _a}b\) xác định khi và chỉ khi \(a > 0,a \ne 1,b > 0\).

Câu 7 :

Chọn đáp án đúng.

  • A
    \({\log _{1000}}{1000^3} = {1000^3}\).
  • B
    \({\log _{1000}}{1000^3} = \frac{1}{3}\).
  • C
    \({\log _{1000}}{1000^3} = 3\).
  • D
    \({\log _{1000}}{1000^3} = {3^{1000}}\).

Đáp án : C

Phương pháp giải :

Với a, b là số thực dương và \(a \ne 1\) thì \({\log _a}{a^b} = b\).

Lời giải chi tiết :

\({\log _{1000}}{1000^3} = 3\)

Câu 8 :

Khẳng định nào sau đây đúng?

  • A
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
  • B
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).
  • C
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
  • D
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\ln a\).

Đáp án : B

Phương pháp giải :

Lôgarit cơ số 10 của số thực dương b được gọi là lôgarit thập phân của b và kí hiệu logb hay lg b.

Lôgarit cơ số e của số thực dương b được gọi là lôgarit tự nhiên của b và kí hiệu ln b.

Lời giải chi tiết :

Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).

Câu 9 :

Giá trị của phép tính \({4^{{{\log }_{\sqrt 2 }}3}}\) là:

  • A
    81.
  • B
    \(9\).
  • C
    \(\frac{1}{{81}}\).
  • D
    \(\frac{1}{9}\).

Đáp án : A

Phương pháp giải :

Với a, b là số thực dương và \(a \ne 1\) thì \({a^{{{\log }_a}b}} = b,{\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b;{\log _a}{b^\alpha } = \alpha {\log _a}b\).

Lời giải chi tiết :

\({4^{{{\log }_{\sqrt 2 }}3}} = {2^{2{{\log }_{{2^{\frac{1}{2}}}}}3}} = {2^{4{{\log }_2}3}} = {2^{{{\log }_2}{3^4}}} = 81\)

Câu 10 :

Chọn đáp án đúng:

  • A
    \({\log _5}15 - 2{\log _5}\sqrt 3  =  - 1\).
  • B
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 1\).
  • C
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 0\).
  • D
    \({\log _5}15 - 2{\log _5}\sqrt 3  = \frac{1}{2}\).

Đáp án : B

Phương pháp giải :

Với a, b là số thực dương và \(a \ne 1\) thì \({\log _a}{b^\alpha } = \alpha {\log _a}b,\log {\,_a}a = 1\)

Với a là số thực dương, \(a \ne 1\), \(M > 0,N > 0\) thì \({\log _a}\frac{M}{N} = {\log _a}M - {\log _a}N\).

Lời giải chi tiết :

\({\log _5}15 - 2{\log _5}\sqrt 3  = {\log _5}15 - {\log _5}3 = {\log _5}\frac{{15}}{3} = {\log _5}5 = 1\)

Câu 11 :

Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng:

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    3.

Đáp án : B

Phương pháp giải :

Đồ thị hàm số hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng 1.

Lời giải chi tiết :

Đồ thị hàm số hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng 1.

Câu 12 :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là:

  • A
    \(D = \left( {0; + \infty } \right)\).
  • B
    \(D = \left( { - \infty ;0} \right)\).
  • C
    \(D = \left( { - \infty ; + \infty } \right)\).
  • D
    Cả A, B, C đều sai.

Đáp án : C

Phương pháp giải :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là \(D = \left( { - \infty ; + \infty } \right)\).

Lời giải chi tiết :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là \(D = \left( { - \infty ; + \infty } \right)\).

Câu 13 :

Hàm số \(y = {\log _2}x\) đồng biến trên khoảng nào sau đây?

  • A
    \(\left( { - 1; + \infty } \right)\).
  • B
    \(\left[ {0; + \infty } \right)\).
  • C
    \(\left[ { - 1; + \infty } \right)\).
  • D
    \(\left( {1; + \infty } \right)\).

Đáp án : D

Phương pháp giải :

Nếu \(a > 1\) thì hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {0; + \infty } \right)\).

Lời giải chi tiết :

Vì \(2 > 1\) nên hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {0; + \infty } \right)\). Do đó, hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {1; + \infty } \right)\)

Câu 14 :

Hàm số nào dưới đây là hàm số mũ?

  • A
    \(y = {x^{\sqrt 2 }}\).
  • B
    \(y = {x^{\log 4}}\).
  • C
    \(y = {\left( {\frac{\pi }{2}} \right)^x}\).
  • D
    \(y = {\log _2}x\).

Đáp án : C

Phương pháp giải :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.

Lời giải chi tiết :

Hàm số \(y = {\left( {\frac{\pi }{2}} \right)^x}\) được gọi là hàm số mũ.

Câu 15 :

Hàm số nào dưới đây có đồ thị như hình dưới?

  • A
    \(y = {3^x}\).
  • B
    \(y = {\left( {\frac{1}{2}} \right)^x}\).
  • C
    \(y = {\left( {\frac{1}{3}} \right)^x}\).
  • D
    \(y = {\left( {\sqrt 2 } \right)^x}\).

Đáp án : C

Phương pháp giải :

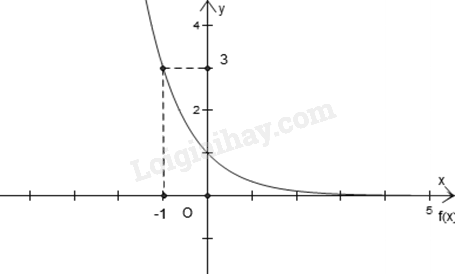
Xét xem đồ thị hàm số nào đi qua điểm \(\left( { - 1;3} \right)\) và (0;1) thì đó là đồ thị hàm số cần tìm.

Lời giải chi tiết :

Ta thấy đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) đi qua điểm \(\left( { - 1;3} \right)\) và (0;1) nên hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) là hàm số cần tìm.

Câu 16 :

Cho hàm số \(f\left( x \right) = {2^x}\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - 2;3} \right]\). Khi đó:

  • A
    \(M.m = 2\).
  • B
    \(M.m = \frac{1}{2}\)
  • C
    \(M.m = 4\).
  • D
    \(M.m = \frac{1}{4}\).

Đáp án : A

Phương pháp giải :

Cho hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\):

+ Nếu \(a > 1\) thì hàm số đồng biến trên \(\mathbb{R}\).

+ Nếu \(0 < a < 1\) thì hàm số nghịch biến trên \(\mathbb{R}\).

Lời giải chi tiết :

Vì \(2 > 1\) nên hàm số \(f\left( x \right) = {2^x}\) đồng biến trên \(\mathbb{R}\).

Do đó, \(\mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right) = {2^3} = 8;\mathop {\min }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( { - 2} \right) = {2^{ - 2}} = \frac{1}{4}\)

Suy ra: \(M = 8,m = \frac{1}{4} \Rightarrow Mm = 8.\frac{1}{4} = 2\).

Câu 17 :

Cho hai biến cố A và B, biến cố hợp của hai biến cố A và B kí hiệu là:

  • A
    \(A \cup B\).
  • B
    \(A \cap B\).
  • C
    AB.
  • D
    \(A + B\).

Đáp án : A

Phương pháp giải :

Biến cố hợp của hai biến cố A và B kí hiệu là \(A \cup B\).

Lời giải chi tiết :

Biến cố hợp của hai biến cố A và B kí hiệu là \(A \cup B\).

Câu 18 :

Trong mẫu số liệu ghép nhóm, tứ phân vị thứ hai \({Q_2}\) bằng:

  • A
    Số trung bình cộng.
  • B
    Mốt.
  • C
    Trung vị.
  • D
    Cả A, B, C đều sai.

Đáp án : C

Phương pháp giải :

Trong mẫu số liệu ghép nhóm, tứ phân vị thứ hai \({Q_2}\) bằng trung vị.

Lời giải chi tiết :

Trong mẫu số liệu ghép nhóm, tứ phân vị thứ hai \({Q_2}\) bằng trung vị.

Câu 19 :

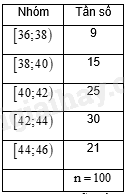
Kết quả kiểm tra môn Toán của lớp 11E được cho ở bảng tần số ghép nhóm sau:

Nhóm nào có tần số bằng 12?

  • A
    \(\left[ {3;5} \right)\).
  • B
    \(\left[ {5;7} \right)\).
  • C
    \(\left[ {7;9} \right)\).
  • D
    \(\left[ {9;11} \right)\).

Đáp án : B

Phương pháp giải :

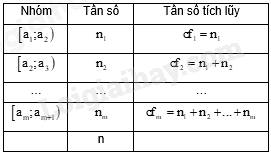
Bảng tần số ghép nhóm cho ở bảng dưới:

Trong đó, mẫu số liệu gồm n số liệu được chia thành m nhóm ứng với m nửa khoảng \(\left[ {{a_1};{a_2}} \right)\); \(\left[ {{a_2};{a_3}} \right)\);...; \(\left[ {{a_m};{a_{m + 1}}} \right)\), ở đó \({a_1} < {a_2} < {a_3} < ... < {a_m} < {a_{m + 1}}\) và \(n = {n_1} + {n_2} + ... + {n_m}\).

Lời giải chi tiết :

Nhóm có tần số bằng 12 là nhóm \(\left[ {5;7} \right)\).

Câu 20 :

Cho hai biến cố A và B. A và B gọi là hai biến cố xung khắc khi:

  • A
    \(A \cap B = \emptyset \).
  • B
    \(A \cap B = A\).
  • C
    \(A \cap B = B\).
  • D
    \(A \cup B = A\).

Đáp án : A

Phương pháp giải :

Cho hai biến cố A và B. Nếu \(A \cap B = \emptyset \) thì A và B gọi là hai biến cố xung khắc.

Lời giải chi tiết :

Cho hai biến cố A và B. Nếu \(A \cap B = \emptyset \) thì A và B gọi là hai biến cố xung khắc.

Câu 21 :

Hai bạn Hạnh và Hà cùng chơi trò chơi bắn cung một cách độc lập. Mỗi bạn chỉ bắn một lần. Xác suất để Hạnh và Hà bắn trúng bia lần lượt là 0,6 và 0,7 trong lần bắn của mình. Xác suất của biến cố: “Bạn Hạnh và bạn Hà đều bắn trượt bia” là:

  • A
    0,4.
  • B
    0,42.
  • C
    0,7
  • D
    0,12.

Đáp án : D

Phương pháp giải :

Nếu hai biến cố A và B độc lập thì \(P\left( {A \cap B} \right) = P\left( A \right).P\left( B \right)\)

Lời giải chi tiết :

Xác suất để Hạnh bắn trượt bia là: \({P_1} = 1 - 0,6 = 0,4\)

Xác suất để Hà bắn trượt bia là: \({P_2} = 1 - 0,7 = 0,3\)

Xác suất để Hạnh và bạn Hà đều bắn trượt bia là: \(0,4.0,3 = 0,12\)

Câu 22 :

Một hộp chứa 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; ...; 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ rút ra là số chia hết cho 3” và biến cố B “Số xuất hiện trên thẻ rút ra là số chia hết cho 4”. Chọn đáp án đúng.

  • A
    \(A \cap B = \left\{ {3;6;9;12;...;48;51} \right\}\).
  • B
    \(A \cap B = \left\{ {4;8;12;16;...;48;52} \right\}\).
  • C
    \(A \cap B = \left\{ {12;24;36;48} \right\}\).
  • D
    Cả A, B, C đều sai.

Đáp án : C

Phương pháp giải :

Cho hai biến cố A và B. Khi đó, A, B là các tập con của không gian mẫu \(\Omega \). Đặt \(D = A \cap B\), ta có D là một biến cố và được gọi là biến cố giao của hai biến cố A và B, kí hiệu là \(A \cap B\) hay AB.

Lời giải chi tiết :

Biến cố \(A \cap B\) là: “Số xuất hiện trên thẻ rút ra là số chia hết cho cả 3 và 4”.

Do đó, \(A \cap B = \left\{ {12;24;36;48} \right\}\).

Câu 23 :

Sau khi điều tra về số học sinh trong 100 lớp học, người ta chia mẫu số liệu đó thành năm nhóm căn cứ vào số lượng học sinh của mỗi lớp (đơn vị: học sinh) và lập bảng tần số ghép nhóm như bảng sau:

Trung vị của mẫu số liệu thuộc là: (làm tròn kết quả đến hàng đơn vị)

  • A
    43.
  • B
    41.
  • C
    42.
  • D
    40.

Đáp án : C

Phương pháp giải :

Bảng tần số ghép nhóm cho ở bảng dưới:

Giả sử nhóm k là nhóm đầu tiên có tần số tích lũy lớn hơn bằng \(\frac{n}{2}\), tức là \(c{f_{k - 1}} < \frac{n}{2}\) nhưng \(c{f_k} \ge \frac{n}{2}\). Ta gọi r, d, \({n_k}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm k, \(c{f_{k - 1}}\) là tần số tích lũy của nhóm \(k - 1\). Trung vị của mẫu số liệu ghép nhóm, kí hiệu \({M_e}\), được tính theo công thức sau: \({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d\).

Lời giải chi tiết :

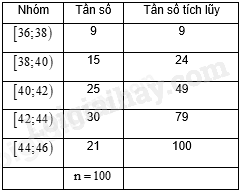
Ta có bảng:

Ta có: \(\frac{n}{2} = 50\) mà \(c{f_3} = 49 < 50 < c{f_4} = 79\). Suy ra, nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 50. Nhóm 4 là nhóm \(\left[ {42;44} \right)\) có \(r = 42,d = 2,{n_4} = 30\) và nhóm 3 là nhóm \(\left[ {40;42} \right)\) có \(c{f_3} = 49\).

Do đó, trung vị của mẫu số liệu là: \({M_e} = 42 + \frac{{50 - 49}}{{30}}.2 \approx 42\) (học sinh)

Câu 24 :

Góc giữa hai đường thẳng a và b có thể bằng:

  • A
    1800.
  • B
    1500.
  • C
    900.
  • D
    Cả A, B, C đều sai.

Đáp án : C

Phương pháp giải :

Góc giữa hai đường thẳng có số đo không vượt quá 900.

Lời giải chi tiết :

Vì góc giữa hai đường thẳng có số đo không vượt quá 900 nên góc giữa hai đường thẳng có thể bằng 900.

Câu 25 :

Trong không gian cho hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đúng?

  • A
    a và b cắt nhau.
  • B
    a và b chéo nhau.
  • C
    a và b cùng nằm trên một mặt phẳng.
  • D
    Góc giữa a và b bằng \({90^0}\).

Đáp án : D

Phương pháp giải :

Hai đường thẳng vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).

Lời giải chi tiết :

Trong không gian cho hai đường thẳng a và b vuông góc với nhau thì góc giữa chúng bằng \({90^0}\).

Câu 26 :

Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = {100^0}\). Góc giữa hai đường thẳng SA và CD bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).

Đáp án : C

Phương pháp giải :

+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).

+ Góc giữa hai đường thẳng không vượt quá \({90^0}\).

Lời giải chi tiết :

Vì ABCD là hình bình hành nên \(AB//CD\)

Do đó, \(\left( {SA,CD} \right) = \left( {SA,AB} \right) = {180^0} - \widehat {SAB} = {80^0}\)

Câu 27 :

Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Khi đó, góc giữa hai đường thẳng AC và MN bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).

Đáp án : B

Phương pháp giải :

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.

Lời giải chi tiết :

Vì M, N lần lượt là trung điểm của các cạnh SB và SD nên MN là đường trung bình của tam giác SBD, do đó, MN//BD.

Vì ABCD là hình thoi nên \(AC \bot BD\)

Vì \(AC \bot BD\), MN//BD nên \(AC \bot MN \Rightarrow \left( {AC,MN} \right) = {90^0}\).

Câu 28 :

Có bao nhiêu mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước?

  • A
    Vô số.
  • B
    1.
  • C
    2.
  • D
    3.

Đáp án : B

Phương pháp giải :

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Lời giải chi tiết :

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Câu 29 :

Chọn đáp án đúng:

  • A
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
  • B
    Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
  • C
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
  • D
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.

Đáp án : A

Phương pháp giải :

Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Lời giải chi tiết :

Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Câu 30 :

Chọn đáp án đúng.

  • A
    Có hai đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • B
    Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • C
    Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • D
    Có ba đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Đáp án : C

Phương pháp giải :

Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Lời giải chi tiết :

Có duy nhất một đường thẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Câu 31 :

Cho đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P. Góc giữa hai đường thẳng d và d’ bằng bao nhiêu độ?

  • A
    \({30^0}\).
  • B
    \({45^0}\).
  • C
    \({60^0}\).
  • D
    \({90^0}\).

Đáp án : D

Phương pháp giải :

Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P nên \(d \bot d' \Rightarrow \left( {d,d'} \right) = {90^0}\)

Câu 32 :

Cho hình chóp S. ABCD có ABCD là hình chữ nhật, SA vuông góc với đáy. Đường thẳng BC vuông góc với mặt phẳng nào?

  • A
    (SAD).
  • B
    (SCD).
  • C
    (SAC).
  • D
    (SAB).

Đáp án : D

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)

Mà ABCD là hình chữ nhật nên \(BC \bot AB\)

Ta có: \(SA \bot BC,BC \bot AB,\) AB và SA cắt nhau tại A và nằm trong mặt phẳng (SAB).

Do đó, \(BC \bot \left( {SAB} \right)\)

Câu 33 :

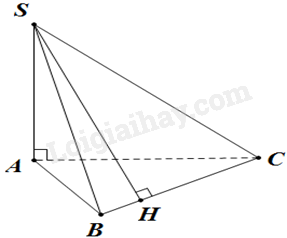
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúng.

  • A
    \(BC \bot AB\).
  • B
    \(BC \bot AH\).
  • C
    \(BC \bot SC\).
  • D
    Cả A, B, C đều sai.

Đáp án : B

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\), mà \(BC \bot SH\) và SA và SH cắt nhau tại S và nằm trong mặt phẳng (SAH) nên \(BC \bot \left( {SAH} \right)\).

Lại có: \(AH \subset \left( {SAH} \right)\) nên \(BC \bot AH\).

Câu 34 :

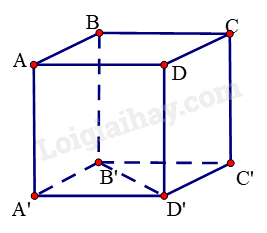
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’A và D’B’ bằng:

  • A
    \({30^0}\).
  • B
    \({60^0}\).
  • C
    \({90^0}\).
  • D
    \({45^0}\).

Đáp án : C

Phương pháp giải :

Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì ABCD.A’B’C’D’ là hình lập phương nên \(AA' \bot \left( {A'B'C'D'} \right)\), mà \(B'D' \subset \left( {A'B'C'D'} \right)\) nên \(AA' \bot B'D'\). Do đó, góc giữa hai đường thẳng A’A và D’B’ bằng \({90^0}\).

Câu 35 :

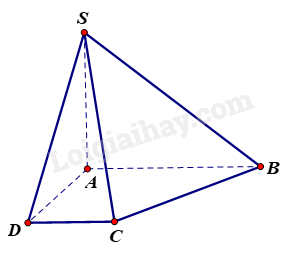
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\). Chọn đáp án đúng.

  • A
    \(\left( {AB,SD} \right) = {90^0}\).
  • B
    \(\left( {AB,SD} \right) = {85^0}\).
  • C
    \(\left( {AB,SD} \right) = {70^0}\).
  • D
    \(\left( {AB,SD} \right) = {75^0}\).

Đáp án : A

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì \(SA \bot \left( {ABCD} \right),AB \subset \left( {ABCD} \right) \Rightarrow SA \bot AB\).

Vì ABCD là hình thang vuông tại A nên \(AB \bot AD\).

Ta có: \(AB \bot AD\), \(SA \bot AB\) và SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD)

Do đó, \(AB \bot \left( {SAD} \right) \Rightarrow AB \bot SD\). Suy ra, \(\left( {AB,SD} \right) = {90^0}\).

II. Tự luận
Câu 1 :

Cho hàm số: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\).

a) Với \(m = \frac{1}{3}\), hãy tìm tập xác định của hàm số trên.

b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định là \(\mathbb{R}\).
Phương pháp giải :

+ Hàm số có dạng \(y = \frac{1}{{\sqrt {u\left( x \right)} }}\) xác định khi \(u\left( x \right) > 0\).

+ Hàm \(y = {\log _a}u\left( x \right)\left( {a > 0,a \ne 1} \right)\) xác định khi \(u\left( x \right) > 0\).

Lời giải chi tiết :

a) Với \(m = \frac{1}{3}\) ta có: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}\).

Hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}\) xác định khi \({\log _3}\left( {{x^2} - 2x + 1} \right) > 0 \Leftrightarrow {x^2} - 2x + 1 > 1 \Leftrightarrow {x^2} - 2x > 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < 0\end{array} \right.\)

Vậy với \(m = \frac{1}{3}\) thì tập xác định của hàm số là: \(D = \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\).

b) Hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\) có tập xác định là \(\mathbb{R}\) khi và chỉ khi \({\log _3}\left( {{x^2} - 2x + 3m} \right) > 0\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow {x^2} - 2x + 3m > 1\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow {x^2} - 2x + 3m - 1 > 0\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow {\left( { - 1} \right)^2} - 3m + 1 < 0 \Leftrightarrow m > \frac{2}{3}\)

Vậy với \(m > \frac{2}{3}\) thì hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\) có tập xác định là \(\mathbb{R}\).

Câu 2 :

Cho hình chóp S. ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC và SD. Chứng minh rằng:

a) \(SC \bot \left( {AHK} \right)\).

b) \(HK \bot \left( {SAC} \right)\) và \(HK \bot AI\).
Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

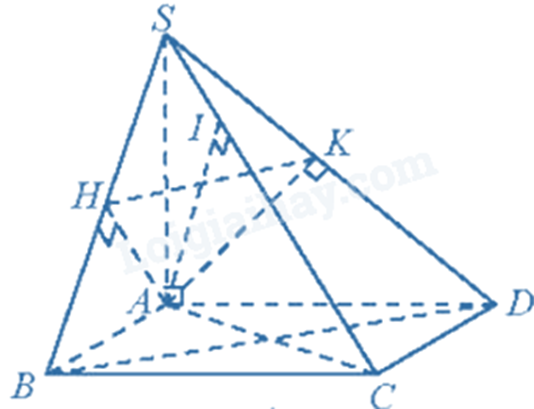
a) Vì \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC\)

Vì ABCD là hình vuông nên \(DC \bot AD\).

Mà SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD). Do đó, \(DC \bot \left( {SAD} \right)\)

Lại có: \(AK \subset \left( {SAD} \right) \Rightarrow DC \bot AK\). Mặt khác, \(AK \bot SD \Rightarrow AK \bot \left( {SDC} \right) \Rightarrow AK \bot SC\)

Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)

Vì ABCD là hình vuông nên \(BC \bot AB\).

Mà SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB). Do đó, \(BC \bot \left( {SAB} \right)\)

Lại có: \(AH \subset \left( {SAB} \right) \Rightarrow BC \bot AH\). Mặt khác, \(AH \bot SB \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\)

Ta có: \(AK \bot SC\), \(AH \bot SC\) và AK và AH cắt nhau tại A nằm trong mặt phẳng (AHK) nên \(SC \bot \left( {AHK} \right)\).

b) Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow \left\{ \begin{array}{l}SA \bot AB\\SA \bot AD\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat {SAB} = {90^0}\\\widehat {SAD} = {90^0}\end{array} \right.\)

Tam giác SAB và tam giác SAD có: SA là cạnh chung, \(\widehat {SAB} = \widehat {SAD} = {90^0}\), \(AB = AD\).

Do đó, \(\Delta SAB = \Delta SAD\left( {c.g.c} \right) \Rightarrow SB = SD\), \(SH = SK\).

Suy ra: \(\frac{{SH}}{{SB}} = \frac{{SK}}{{SD}}\). Do đó, HK//BD (1)

Vì ABCD là hình vuông nên \(AC \bot BD\).

Vì \(SA \bot \left( {ABCD} \right),DB \subset \left( {ABCD} \right) \Rightarrow SA \bot DB\)

Mà SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên \(DB \bot \left( {SAC} \right)\) (2)

Từ (1) và (2) ta có: \(HK \bot \left( {SAC} \right)\). Mà \(AI \subset \left( {SAC} \right)\), suy ra \(HK \bot AI\).

Câu 3 :

So sánh các số sau: \(A = \frac{1}{{1000}};B = {\left( {\frac{{99}}{{1000}}} \right)^3};C = {\left( {\frac{1}{{{{11}^2}}} + \frac{1}{{{{12}^2}}} + ... + \frac{1}{{{{1000}^2}}}} \right)^3}\).
Phương pháp giải :

Nếu \(n > 0\) thì \(a > b > 0 \Rightarrow {a^n} > {b^n}\)

Lời giải chi tiết :

Do \(0 < \frac{{99}}{{1000}} < \frac{{100}}{{1000}} = \frac{1}{{10}} < 1 \Rightarrow {\left( {\frac{{99}}{{1000}}} \right)^3} < {\left( {\frac{1}{{10}}} \right)^3} \Rightarrow B < A\left( 1 \right)\)

Với \(n \in \mathbb{N}*,n > 1\) ta có: \(\frac{1}{{n - 1}} - \frac{1}{n} = \frac{{n - \left( {n - 1} \right)}}{{n\left( {n - 1} \right)}} = \frac{1}{{n\left( {n - 1} \right)}} > \frac{1}{{{n^2}}} \Rightarrow \frac{1}{{{n^2}}} < \frac{1}{{n - 1}} - \frac{1}{n}\)

Do đó, \(\frac{1}{{{{11}^2}}} < \frac{1}{{10}} - \frac{1}{{11}};\frac{1}{{{{12}^2}}} < \frac{1}{{11}} - \frac{1}{{12}};...;\frac{1}{{{{1000}^2}}} < \frac{1}{{999}} - \frac{1}{{1000}}\)

\( \Rightarrow \frac{1}{{{{11}^2}}} + \frac{1}{{{{12}^2}}} + ... + \frac{1}{{{{1000}^2}}} < \frac{1}{{10}} - \frac{1}{{11}} + \frac{1}{{11}} - \frac{1}{{12}} + ... + \frac{1}{{999}} - \frac{1}{{1000}} = \frac{1}{{10}} - \frac{1}{{1000}} = \frac{{99}}{{1000}}\)

\( \Rightarrow {\left( {\frac{1}{{{{11}^2}}} + \frac{1}{{{{12}^2}}} + ... + \frac{1}{{{{1000}^2}}}} \right)^3} < {\left( {\frac{{99}}{{1000}}} \right)^3} \Rightarrow C < B\left( 2 \right)\)

Từ (1) và (2) ta có: \(C < B < A\).

Bài liên quan
close