Đề thi, đề kiểm tra Toán lớp 11 - Cánh diều

Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 7

Tải về

Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng.

Đề bài

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1 :

Cho a là một số dương, biểu thức ${a^{\frac{{ - 5}}{{12}}}}.\sqrt a .\frac{1}{{{a^2}}}$ viết dưới dạng lũy thừa với số mũ hữu tỉ là

A

${a^{\frac{{ - 5}}{{12}}}}$
B

${a^{\frac{{ - 10}}{{12}}}}$
C

${a^{\frac{{ - 23}}{{12}}}}$
D

${a^2}$

Câu 2 :

Với a, b là các số thực dương tùy ý thỏa mãn $a \ne 1$ và ${\log _a}b = 2$ , giá trị của ${\log _{{a^2}}}\left( {a{b^2}} \right)$ bằng

A

$2$
B

$\frac{3}{2}$
C

$\frac{1}{2}$
D

$\frac{5}{2}$

Câu 3 :

Tập xác định của hàm số $y = {\left( {x - 1} \right)^{\frac{1}{3}}}$ là

A

$\left[ {1; + \infty } \right)$
B

$\left( {1; + \infty } \right)$
C

$\mathbb{R}$
D

Một đáp án khác

Quảng cáo

Câu 4 :

Nghiệm của phương trình ${\log _3}(5x) = 2$ là

A

$x = \frac{8}{5}$
B

$x = 9$
C

$x = \frac{9}{5}$
D

$x = 8$

Câu 5 :

Xét phép thử chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có một chữ số và hai biến cố A = {0;2;4;6;8} và B = {0;3;6;9}. Hỏi biến cố C là hợp của hai biến cố A và B là tập hợp gồm bao nhiêu phần tử?

A

7
B

9
C

6
D

8

Câu 6 :

Xét một phép thử có hai biến cố A và B là độc lập với nhau và $P(A) = \frac{1}{5}$ ; $P(B) = \frac{2}{3}$ . Tính P(AB).

A

$\frac{2}{5}$
B

$\frac{{13}}{{15}}$
C

$\frac{2}{{15}}$
D

$\frac{7}{{15}}$

Câu 7 :

Thống kê chiều cao của học sinh lớp 11A ta có bảng số liệu sau:

Hỏi lớp có bao nhiêu học sinh có chiều cao từ 168 cm trở lên?

A

11
B

20
C

31
D

8

Câu 8 :

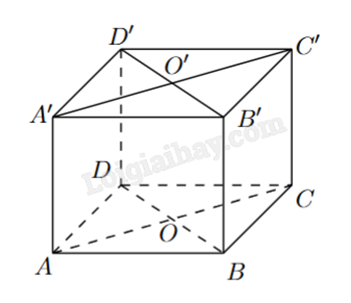
Cho hình lập phương ABCS.A’B’C’D’. Số đo góc tạo bởi hai đường thẳng BD và CC’ bằng

A

${90^o}$
B

${60^o}$
C

${45^o}$
D

${120^o}$

Câu 9 :

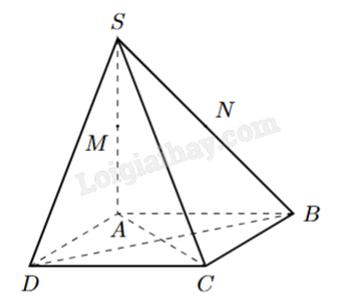
Cho chóp S.ABCD có đáy là hình chữ nhật và $SA \bot (ABCD)$ . Gọi M, N lần lượt là trung điểm của SA, SB. Đường thẳng vuông góc với MN là

A

AD
B

SB
C

CD
D

SC

Câu 10 :

Tìm mệnh đề đúng.

A

Hình hộp có đáy là hình chữ nhật
B

Hình lăng trụ đều có đáy là tam giác đều
C

Hình chóp đều có tất cả các cạnh bằng nhau
D

Hình lập phương có 6 mặt là hình vuông

Câu 11 :

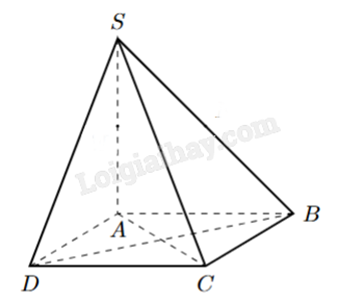
Cho hình chóp.S ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD). Hình chiếu vuông góc của DSCD lên mặt phẳng (ABCD) là

A

$\Delta ABC$
B

$\Delta ACD$
C

$\Delta SAD$
D

$\Delta SBA$

Câu 12 :

Trong không gian cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó $a \bot (P)$ . Mệnh đề nào sau đây sai?

A

Nếu b // a thì $b \bot (P)$
B

Nếu $b \bot a$ thì b // (P)
C

Nếu b // (P) thì $b \bot a$
D

Nếu $b \bot (P)$ thì b // a

Phần II: Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1, câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1 :

Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:

a) Cỡ mẫu là n = 50.

Đúng

Sai

b) Nhóm chứa mốt của mẫu số liệu là [8;8,5).

Đúng

Sai

c) Mốt của mẫu số liệu bằng ${M_o} = 8,12$ .

Đúng

Sai

d) Số trung bình của mẫu số liệu làm tròn đến hàng phần nghìn là $\overline x = 8,122$ .

Đúng

Sai

Câu 2 :

Cho hình lập phương ABCD.A’B’C’D’. Gọi O và O’ lần lượt là tâm của ABCD và A’B’C’D’.

a) $AD \bot (CDD'C')$ .

Đúng

Sai

b) Góc giữa hai đường thẳng A’D và DC’ là ${60^o}$ .

Đúng

Sai

c) $OO' \bot (ABCD)$ .

Đúng

Sai

d) $A'D \bot BB'$ .

Đúng

Sai

Phần III: Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1 :

Nếu khối lượng carbon-14 trong cơ thể sinh vật lúc chết là ${M_0}$ (g) thì khối lượng carbon-14 còn lại (tính theo gam) sau t năm được tính theo công thức $M(t) = {M_0}{\left( {\frac{1}{2}} \right)^{\frac{1}{T}}}$ (g), trong đó T = 7530 (năm) là chu kì bán rã của carbon-14. Nghiên cứu hoá thạch của một sinh vật, người ta xác định được khối lượng carbon-14 hiện có trong hoá thạch là ${5.10^{ - 13}}$ g. Nhờ biết tỉ lệ khối lượng của carbon- 14 so với carbon- 12 trong cơ thể sinh vật sống, người ta xác định được khối lượng carbon-14 trong cơ thể lúc sinh vật chết là ${M_0} = 1,{2.10^{ - 12}}$ g. Sinh vật này sống cách đây bao nhiêu năm (làm tròn kết quả đến hàng trăm)?

Đáp án:

Câu 2 :

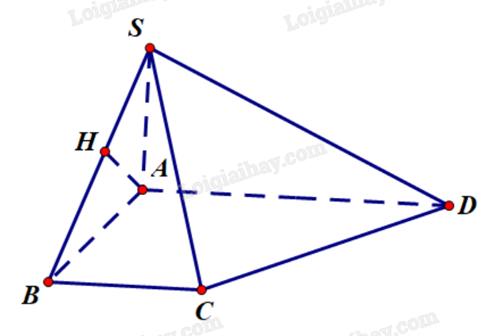
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với AB = BC = 1, AD = 2. Biết $SA \bot (ABCD)$ và SA = 1. Tính khoảng cách giữa AD và SB (tính chính xác đến hàng phần trăm).

Đáp án:

Quảng cáo

Câu 3 :

Một bệnh truyền nhiễm có xác suất lây bệnh là 0,9 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,15 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Anh Hà tiếp xúc với một người bệnh hai lần, trong đó có một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất anh Hà bị lây bệnh từ người bệnh mà anh tiếp xúc đó (làm tròn đến hàng phần trăm).

Đáp án:

Câu 4 :

Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở bảng sau:

Tứ phân vị thứ ba của mẫu số liệu bằng bao nhiêu?

Đáp án:

Phần IV: Tự luận.

Thí sinh trình bày lời giải từ câu 1 đến câu 3.

Câu 1 :

Đặt $a = {\log _2}3$ , $a = {\log _5}3$ . Biểu thị ${\log _6}45$ theo a và b.

Câu 2 :

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Tính góc giữa AC và mặt phẳng (ABB’A’).

Câu 3 :

Sự tăng trưởng của một loài vi khuẩn được tính theo công thức $f(t) = A.{e^{rt}}$ , trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng (r > 0), t (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao nhiêu giờ thì số lượng vi khuẩn tăng gấp 10 lần (làm tròn đến hàng phần mười)?

Quảng cáo

Lời giải và đáp án

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1 :

Cho a là một số dương, biểu thức ${a^{\frac{{ - 5}}{{12}}}}.\sqrt a .\frac{1}{{{a^2}}}$ viết dưới dạng lũy thừa với số mũ hữu tỉ là

A

${a^{\frac{{ - 5}}{{12}}}}$
B

${a^{\frac{{ - 10}}{{12}}}}$
C

${a^{\frac{{ - 23}}{{12}}}}$
D

${a^2}$

Đáp án : C

Phương pháp giải :

Áp dụng công thức ${x^m}.{x^n} = {x^{m + n}}$ , $\sqrt[b]{{{x^a}}} = {x^{\frac{a}{b}}}$ .

Lời giải chi tiết :

${a^{\frac{{ - 5}}{{12}}}}.\sqrt a .\frac{1}{{{a^2}}} = {a^{\frac{{ - 5}}{{12}}}}.{a^{\frac{1}{2}}}.{a^{ - 2}} = {a^{\frac{{ - 5}}{{12}} + \frac{1}{2} - 2}} = {a^{\frac{{ - 23}}{{12}}}}$ .

Câu 2 :

Với a, b là các số thực dương tùy ý thỏa mãn $a \ne 1$ và ${\log _a}b = 2$ , giá trị của ${\log _{{a^2}}}\left( {a{b^2}} \right)$ bằng

A

$2$
B

$\frac{3}{2}$
C

$\frac{1}{2}$
D

$\frac{5}{2}$

Đáp án : B

Phương pháp giải :

Áp dụng công thức ${\log _{{a^m}}}b = \frac{1}{m}{\log _a}b$ ; ${\log _a}{b^m} = m{\log _a}b$ ; ${\log _a}bc = {\log _a}b + {\log _a}c$ .

Lời giải chi tiết :

${\log _{{a^2}}}\left( {a{b^2}} \right) = \frac{1}{2}{\log _a}\left( {a{b^2}} \right) = \frac{1}{2}{\log _a}a + \frac{1}{2}{\log _a}{b^2} = \frac{1}{2}{\log _a}a + 2.\frac{1}{2}{\log _a}b$

$= \frac{1}{2}{\log _a}a + {\log _a}b = \frac{1}{2}.1 + 2 = \frac{3}{2}$ .

Câu 3 :

Tập xác định của hàm số $y = {\left( {x - 1} \right)^{\frac{1}{3}}}$ là

A

$\left[ {1; + \infty } \right)$
B

$\left( {1; + \infty } \right)$
C

$\mathbb{R}$
D

Một đáp án khác

Đáp án : B

Phương pháp giải :

Tập xác định của hàm số $y = {x^\alpha }$ là $\left( {0; + \infty } \right)$ nếu $\alpha$ không nguyên.

Lời giải chi tiết :

ĐKXĐ: $x - 1 > 0 \Leftrightarrow x > 1$ .

Vậy $D = \left( {1; + \infty } \right)$ .

Câu 4 :

Nghiệm của phương trình ${\log _3}(5x) = 2$ là

A

$x = \frac{8}{5}$
B

$x = 9$
C

$x = \frac{9}{5}$
D

$x = 8$

Đáp án : C

Phương pháp giải :

${\log _a}x = b \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x = {a^b}\end{array} \right.$ .

Lời giải chi tiết :

${\log _3}(5x) = 2 \Leftrightarrow \left\{ \begin{array}{l}5x > 0\\5x = {3^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x = \frac{9}{5}\end{array} \right. \Leftrightarrow x = \frac{9}{5}$ .

Câu 5 :

A

7
B

9
C

6
D

8

Đáp án : A

Phương pháp giải :

Hợp của hai tập hợp là tập hợp gồm các phần tử thuộc A, thuộc B hoặc thuộc cả A và B.

Lời giải chi tiết :

$C = A \cap B = \{ 0;2;3;4;6;8;9\}$ .

Câu 6 :

Xét một phép thử có hai biến cố A và B là độc lập với nhau và $P(A) = \frac{1}{5}$ ; $P(B) = \frac{2}{3}$ . Tính P(AB).

A

$\frac{2}{5}$
B

$\frac{{13}}{{15}}$
C

$\frac{2}{{15}}$
D

$\frac{7}{{15}}$

Đáp án : C

Phương pháp giải :

Với hai biến cố độc lập A, B, ta có P(AB) = P(A).P(B).

Lời giải chi tiết :

$P(AB) = P(A).P(B) = \frac{1}{5}.\frac{2}{3} = \frac{2}{{15}}$ .

Câu 7 :

Thống kê chiều cao của học sinh lớp 11A ta có bảng số liệu sau:

Hỏi lớp có bao nhiêu học sinh có chiều cao từ 168 cm trở lên?

A

11
B

20
C

31
D

8

Đáp án : A

Phương pháp giải :

Số học sinh cần tìm là tổng tần số của các nhóm chứa giá trị từ 168 cm trở lên

Lời giải chi tiết :

Số học sinh có chiều cao từ 168 cm trở lên là 8 + 3 = 11.

Câu 8 :

Cho hình lập phương ABCS.A’B’C’D’. Số đo góc tạo bởi hai đường thẳng BD và CC’ bằng

A

${90^o}$
B

${60^o}$
C

${45^o}$
D

${120^o}$

Đáp án : A

Phương pháp giải :

Nếu a // b thì (a,c) = (b,c).

Lời giải chi tiết :

Vì CC’ // BB’ nên $(BD,CC') = (BD,BB') = \widehat {B'BD}$ .

Vì $BB' \bot (ABCD)$ nên $BB' \bot BD$ hay $\widehat {B'BD} = {90^o}$ .

Câu 9 :

Cho chóp S.ABCD có đáy là hình chữ nhật và $SA \bot (ABCD)$ . Gọi M, N lần lượt là trung điểm của SA, SB. Đường thẳng vuông góc với MN là

A

AD
B

SB
C

CD
D

SC

Đáp án : A

Phương pháp giải :

Chứng minh mặt phẳng chứa MN vuông góc với một trong số các đường thẳng ở đáp án rồi kết luận.

Lời giải chi tiết :

Ta có $\left\{ \begin{array}{l}SA \bot (ABCD) \Rightarrow SA \bot AD\\AD \bot AB\end{array} \right. \Rightarrow AD \bot (SAB) \Rightarrow AD \bot MN$ (vì M, N thuộc (SAB)).

Câu 10 :

Tìm mệnh đề đúng.

A

Hình hộp có đáy là hình chữ nhật
B

Hình lăng trụ đều có đáy là tam giác đều
C

Hình chóp đều có tất cả các cạnh bằng nhau
D

Hình lập phương có 6 mặt là hình vuông

Đáp án : D

Phương pháp giải :

Dựa vào định nghĩa hình hộp, hình lăng trụ đều, hình chóp đều, hình lập phương.

Lời giải chi tiết :

“Hình lập phương có 6 mặt là hình vuông” là mệnh đề đúng.

A sai vì hình hộp có đáy là hình bình hành.

B sai vì hình lăng trụ đều có đáy là đa giác đều

C sai vì hình chóp đều là hình chóp có đáy là đa giác đều, các cạnh bên bằng nhau.

Câu 11 :

Cho hình chóp.S ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD). Hình chiếu vuông góc của DSCD lên mặt phẳng (ABCD) là

A

$\Delta ABC$
B

$\Delta ACD$
C

$\Delta SAD$
D

$\Delta SBA$

Đáp án : B

Phương pháp giải :

Tìm hình chiếu vuông góc của các điểm S, C, D lên (ABCD).

Lời giải chi tiết :

Hình chiếu vuông góc của các điểm S, C, D lên mặt phẳng (ABCD) lần lượt là A, C, D.

Suy ra hình chiếu vuông góc của DSCD lên mặt phẳng (ABCD) là DACD.

Câu 12 :

Trong không gian cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó $a \bot (P)$ . Mệnh đề nào sau đây sai?

A

Nếu b // a thì $b \bot (P)$
B

Nếu $b \bot a$ thì b // (P)
C

Nếu b // (P) thì $b \bot a$
D

Nếu $b \bot (P)$ thì b // a

Đáp án : B

Phương pháp giải :

Áp dụng liên hệ giữa quan hệ vuông góc và quan hệ song song.

Lời giải chi tiết :

B sai vì nếu $b \bot a$ thì b // (P) hoặc b thuộc (P).

Phần II: Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1, câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1 :

Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:

a) Cỡ mẫu là n = 50.

Đúng

Sai

b) Nhóm chứa mốt của mẫu số liệu là [8;8,5).

Đúng

Sai

c) Mốt của mẫu số liệu bằng ${M_o} = 8,12$ .

Đúng

Sai

d) Số trung bình của mẫu số liệu làm tròn đến hàng phần nghìn là $\overline x = 8,122$ .

Đúng

Sai

Đáp án

a) Cỡ mẫu là n = 50.

Đúng

Sai

b) Nhóm chứa mốt của mẫu số liệu là [8;8,5).

Đúng

Sai

c) Mốt của mẫu số liệu bằng ${M_o} = 8,12$ .

Đúng

Sai

d) Số trung bình của mẫu số liệu làm tròn đến hàng phần nghìn là $\overline x = 8,122$ .

Đúng

Sai

Phương pháp giải :

a) Cỡ mẫu bằng tổng tần số trong bảng số liệu.

b) Nhóm chứa mốt có tần số lớn nhất trong bảng số liệu.

c) Công thức tính mốt thuộc nhóm $[{u_m};{u_{m + 1}})$ :

${M_o} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right)\left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)$ ; trong đó ${n_m}$ là tần số nhóm thứ m.

d) Công thức tính số trung bình: $\overline x = \frac{{{c_1}{n_1} + {c_2}{n_2}... + {c_n}{n_k}}}{N}$ ; trong đó N là kích thước của bảng tần số k nhóm, ${n_i}$ là tần số nhóm i, ${c_i}$ là giá trị đại diện nhóm i $(1 \le i \le k)$ .

Lời giải chi tiết :

a) Sai. n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82.

b) Đúng. Nhóm chứa mốt là [8;8,5).

c) Sai. ${M_o} = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right)\left( {24 - 13} \right)}}.\left( {8,5 - 8} \right) = \frac{{177}}{{22}} = 8,0(45)$ .

d) Đúng. $\overline x = \frac{{6,75.8 + 7,25.10 + 7,75.16 + 8,25.24 + 8,75.13 + 9,25.7 + 9,75.4}}{{82}} = \frac{{333}}{{41}} \approx 8,122$ .

Câu 2 :

Cho hình lập phương ABCD.A’B’C’D’. Gọi O và O’ lần lượt là tâm của ABCD và A’B’C’D’.

a) $AD \bot (CDD'C')$ .

Đúng

Sai

b) Góc giữa hai đường thẳng A’D và DC’ là ${60^o}$ .

Đúng

Sai

c) $OO' \bot (ABCD)$ .

Đúng

Sai

d) $A'D \bot BB'$ .

Đúng

Sai

Đáp án

a) $AD \bot (CDD'C')$ .

Đúng

Sai

b) Góc giữa hai đường thẳng A’D và DC’ là ${60^o}$ .

Đúng

Sai

c) $OO' \bot (ABCD)$ .

Đúng

Sai

d) $A'D \bot BB'$ .

Đúng

Sai

Phương pháp giải :

Áp dụng điều kiện để đường thẳng vuông góc với mặt phẳng; quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.

Lời giải chi tiết :

a) Đúng. Ta có $\left\{ \begin{array}{l}AD \bot DC\\AD \bot DD'\end{array} \right. \Rightarrow AD \bot (CDD'C')$ .

b) Đúng. Ta có A’D = DC’ = A’C’ (đường chéo của các hình vuông bằng nhau) nên A’DC’ là hình tam giác đều, hay $\widehat {A'DC'} = {60^o}$ .

Vậy $(A'D,DC') = \widehat {A'DC'} = {60^o}$ .

c) Đúng. Dễ thấy mặt phẳng (ACC’A’) là hình chữ nhật có O là trung điểm của AC, O’ là trung điểm của A’C’. Khi đó OO’ // AA’ và cùng vuông góc với mặt phẳng đáy (ABCD).

d) Sai. $(A'D,BB') = (A'D,DD') = \widehat {A'DD'} = {45^o}$ .

Phần III: Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Thay các giá trị từ đề bài vào công thức đã cho. Áp dụng quy tắc biến đổi phương trình mũ và phương trình logarit.

Lời giải chi tiết :

${5.10^{ - 13}} = 1,{2.10^{ - 12}}{\left( {\frac{1}{2}} \right)^{\frac{t}{{5730}}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{{5730}}}} = \frac{5}{{12}} \Leftrightarrow \frac{t}{{5730}} = {\log _{\frac{1}{2}}}\frac{5}{{12}} \Leftrightarrow t = 5730{\log _{\frac{1}{2}}}\frac{5}{{12}} \approx 7200$ (năm).

Câu 2 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Tính độ dài đoạn vuông góc chung của hai đường thẳng.

Lời giải chi tiết :

Kẻ $AH \bot SB$ , H thuộc SB.

Vì $SA \bot (ABCD)$ nên $SA \bot AD$ .

Ta có $\left\{ \begin{array}{l}AD \bot SA\\AD \bot AB\end{array} \right. \Rightarrow AD \bot (SAB) \Rightarrow AD \bot AH$ .

Do đó, AH là đoạn vuông góc chung của SB và AD.

Xét tam giác SAB vuông tại A có đường cao AH:

$\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} \Leftrightarrow \frac{1}{{A{H^2}}} = \frac{1}{{{1^2}}} + \frac{1}{{{1^2}}} = 2 \Leftrightarrow A{H^2} = \frac{1}{2} \Leftrightarrow AH = \frac{{\sqrt 2 }}{2} \approx 0,71$ .

Vậy $d\left( {AD,SB} \right) = AH \approx 0,71$ .

Câu 3 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Vẽ sơ đồ hình cây.

Lời giải chi tiết :

Việc đeo khẩu trang ở lần trước hay lần sau gặp không ảnh hưởng đến xác suất nhiễm bệnh mỗi lần gặp nhau. Giả sử anh Hà lần đầu không đeo khẩu trang. Ta có:

Xác suất anh Hà nhiễm bệnh là: $0,9 + 0,1.0,15 = 0,915 \approx 0,92$ .

Câu 4 :

Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở bảng sau:

Tứ phân vị thứ ba của mẫu số liệu bằng bao nhiêu?

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Tính ${Q_3}$ .

Lời giải chi tiết :

Cỡ mẫu: n = 8 + 10 + 7 + 5 + 2 + 1 = 33.

Gọi ${x_1};{x_2};...;{x_{33}}$ là số thời gian thực hiện cuộc gọi sắp xếp theo thứ tự không giảm.

${Q_3} = \frac{{{x_{25}} + {x_{26}}}}{2}$ .

Vì ${x_{25}} \in [120;180)$ và ${x_{26}} \in [180;240)$ nên ${Q_3} = 180$ .

Phần IV: Tự luận.

Thí sinh trình bày lời giải từ câu 1 đến câu 3.

Câu 1 :

Đặt $a = {\log _2}3$ , $a = {\log _5}3$ . Biểu thị ${\log _6}45$ theo a và b.

Phương pháp giải :

Áp dụng các công thức biến đổi logarit ${\log _a}b = \frac{a}{{{{\log }_b}a}}$ ; $m{\log _a}b = {\log _a}{b^m}$ ; ${\log _a}b.{\log _b}c = {\log _a}c$ .

Lời giải chi tiết :

${\log _6}45 = \frac{{{{\log }_2}45}}{{{{\log }_2}6}} = \frac{{{{\log }_2}{3^2}.5}}{{{{\log }_2}2.3}} = \frac{{{{\log }_2}{3^2} + {{\log }_2}5}}{{{{\log }_2}2 + {{\log }_2}3}} = \frac{{2{{\log }_2}3 + {{\log }_2}3.{{\log }_3}5}}{{{{\log }_2}2 + {{\log }_2}3}}$

$= \frac{{2{{\log }_2}3 + {{\log }_2}3.\frac{1}{{{{\log }_5}3}}}}{{{{\log }_2}2 + {{\log }_2}3}} = \frac{{2a + \frac{a}{b}}}{{1 + a}} = \frac{{2ab + a}}{{b(1 + a)}} = \frac{{2ab + a}}{{ab + b}}$ .

Câu 2 :

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Tính góc giữa AC và mặt phẳng (ABB’A’).

Phương pháp giải :

Xác định hình chiếu vuông góc của AC lên mặt phẳng (ABB’A).

Lời giải chi tiết :

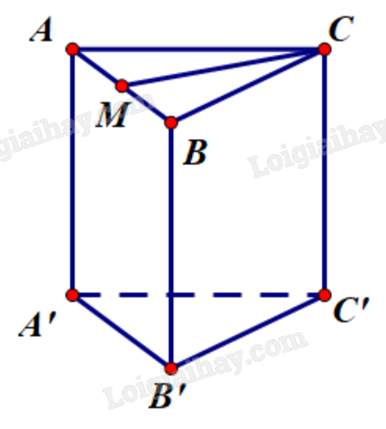
Gọi M là trung điểm của AB. Vì tam giác ABC đều nên CM vừa là đường trung tuyến, vừa là đường cao của tam giác ABC.

Ta có ABC.A’B’C’ là hình lăng trụ đứng nên $AA' \bot (ABC) \Rightarrow AA' \bot CM$ .

Mặt khác $\left\{ \begin{array}{l}AA' \bot CM\\AB \bot CM\end{array} \right. \Rightarrow CM \bot (AA'B'B)$ .

Mà M thuộc (AA’B’B) nên M là hình chiếu vuông góc của C lên (AA’B’B).

Do đó, AM là hình chiếu vuông góc của AC lên (AA’B’B).

Vậy góc giữa AC và mặt phẳng (AA’B’B) là $\widehat {CAM} = {60^o}$ (vì tam giác ABC đều).

Câu 3 :

Phương pháp giải :

Thay số từ dữ kiện của đề bài vào công thức $f(t) = A.{e^{rt}}$ , tính r. Từ r, tính thời gian để số lượng vi khuẩn tăng gấp 10 lần.

Lời giải chi tiết :

Số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con nên:

$f(10) = 5000 \Leftrightarrow 1000.{e^{10r}} = 5000 \Leftrightarrow {e^{10r}} = 5 \Leftrightarrow 10r = \ln 5 \Leftrightarrow r = \frac{{\ln 5}}{{10}}$ .

Số vi khuẩn tăng gấp 10 lần sẽ được 1000.10 = 10000 con. Ta có:

$f(t) = 10000 \Leftrightarrow 1000.{e^{\frac{{\ln 5}}{{10}}t}} = 10000 \Leftrightarrow {e^{\frac{{\ln 5}}{{10}}t}} = 10 \Leftrightarrow \frac{{\ln 5}}{{10}}t = \ln 10 \Leftrightarrow t = \frac{{10\ln 10}}{{\ln 5}} \approx 14,3$ (giờ).

Bài liên quan

Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 8

Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng.
Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 6

Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng.
Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 5

Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng. Với a là số thực khác 0 thì:
Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 4

Phần trắc nghiệm (7 điểm) Câu 1: Khẳng định nào sau đây là đúng?
Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 3

Phần trắc nghiệm (7 điểm) Câu 1: Cho $a>0,m,n\in \mathbb{R}$ . Khẳng định nào sau đây là đúng?