Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 2Tải về Câu 1: Cho các câu sau: (1) Số 7 là số lẻ. (2) Bài toán này khó quá! (3) Cuối tuần này bạn có rảnh không? (4) Số 10 là một số nguyên tố. Trong các câu trên có bao nhiêu câu là mệnh đề? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài I. Trắc nghiệm (7 điểm) Câu 1: Cho các câu sau: (1) Số 7 là số lẻ. (2) Bài toán này khó quá! (3) Cuối tuần này bạn có rảnh không? (4) Số 10 là một số nguyên tố. Trong các câu trên có bao nhiêu câu là mệnh đề? A. 1. B. 2. C. 3. D. 4. Câu 2: Mệnh đề phủ định của mệnh đề “\(\forall x \in \mathbb{R},\,\,x - 2 > 5\)” là: A. “\(\exists x \in \mathbb{R},\,\,x - 2 \le 5\)”. B. “\(\exists x \in \mathbb{R},\,\,x - 2 \ge 5\)”. C. “\(\forall x \in \mathbb{R},\,\,x - 2 \le 5\)”. D. “\(\forall x \in \mathbb{R},\,\,x - 2 \ge 5\)”. Câu 3: Cho tập hợp \(D = \left\{ {x \in {\mathbb{N}^*}|x\left( {x - 2} \right)\left( {x - 3} \right) = 0} \right\}\). Viết lại tập hợp D dưới dạng liệt kê các phần tử của tập hợp đó. A. D = {2;3}. B. D = {0;1;2}. C. D = {1;2}. D. D = {0;2;3}. Câu 4: Xác định tập hợp B = {3;6;9;12;15} bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp. A. \(B = \left\{ {3n|n \in \mathbb{N},\,\,1 \le n \le 5} \right\}\). B. \(B = \left\{ {n|n\,\, \vdots \,\,3} \right\}\). C. \(B = \left\{ {3n|n \in \mathbb{N},\,\,1 < n < 5} \right\}\). D. \(B = \left\{ {n|n \in \mathbb{N},\,\,0 \le n \le 5} \right\}\). Câu 5: Cho hai tập hợp \(A = \left( { - \infty ; - 2} \right]\) và \(B = \left( { - 3;5} \right]\). Tìm mệnh đề sai. A. \(A \cap B = \left( { - 3; - 2} \right].\) B. \(A\backslash B = \left( { - \infty ; - 3} \right)\). C. \(A \cup B = \left( { - \infty ;5} \right]\). D. \(B\backslash A = \left( { - 2;5} \right]\). Câu 6: Trong các tập hợp sau, tập hợp nào là tập con của tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\)? A. \({A_1} = \left\{ {1;6} \right\}.\) B. \({A_2} = \left\{ {0;1;3} \right\}.\) C. \({A_3} = \left\{ {4;5} \right\}.\) D. \({A_4} = \left\{ 0 \right\}.\) Câu 7: Trong các mệnh đề dưới đây, mệnh đề nào đúng? A. 12 là số nguyên tố. B. 9 là số nguyên tố. C. 4 là số nguyên tố. D. 5 là số nguyên tố. Câu 8: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. \(2{x^3} + 1 \ge y + 2{x^2}.\) B. \(2x - 6y + 5 < 2x - 6y + 3.\) C. \(2{x^2} + 1 \ge y + 2{x^2}.\) D. \(4{x^2} < 2x + 5y - 6.\) Câu 9: Điểm nào dưới đây thuộc miền nghiệm của bất phương trình \(3x + 2y < 10\)? A. (5;1). B. (4;2). C. (1;5). D. (1;2). Câu 10: Trong tam giác EFG, chọn mệnh đề đúng. A. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos G.\) B. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos E.\) C. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos E.\) D. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G.\) Câu 11: Cho tam giác ABC biết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \) và \(AB = 2\sqrt 2 \). Tính AC. A. \(2\sqrt 3 .\) B. \(2\sqrt 5 .\) C. \(2\sqrt 2 .\) D. \(2\sqrt 6 .\) Câu 12: Cho tam giác ABC có b = 7, c = 5, \(\cos A = \frac{3}{5}.\) Độ dài đường cao \({h_a}\) của tam giác ABC là: A. \(8.\) B. \(8\sqrt 3 .\) C. \(\frac{{7\sqrt 2 }}{2}.\) D. \(7\sqrt 2 .\) Câu 13: Với giá trị nào của x sau đây, mệnh đề chứa biến P(x): “\({x^2} - 5x + 4 = 0\)” là mệnh đề đúng? A. 0. B. \(\frac{4}{5}\). C. 5. D. 1. Câu 14: Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn? A. \(\left\{ \begin{array}{l}{x^2} - 4 \ge 0\\3x + 4y < 2\end{array} \right.\). B. \(x - y > 0\). C. \(\left\{ \begin{array}{l}{y^2} + 2y - 3 > 0\\5x - y > 2\end{array} \right.\). D. \(\left\{ \begin{array}{l}x - 4 \ge y\\3x + 4y < 5\end{array} \right.\). Câu 15: Giá trị của biểu thức \(T = 2 + {\sin ^2}{90^0} + 2{\cos ^2}{60^0} - 3{\tan ^2}{45^0}\) bằng: A. 3. B. \( - \frac{1}{2}\). C. 1. D. \(\frac{1}{2}\). Câu 16: Cho tam giác ABC có BC = a, AC = b, AB = c, có R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và hc là độ dài đường cao xuất phát từ đỉnh C. Chọn mệnh đề sai. A. \({S_{ABC}} = ab\sin C.\) B. \({S_{ABC}} = pr.\) C. \({S_{ABC}} = \frac{{abc}}{{4R}}.\) D. \({S_{ABC}} = \frac{1}{2}c.{h_c}.\) Câu 17: Tam giác ABC có BC = 1, AC = 3, \(\angle C = {60^0}\). Tính độ dài cạnh AB. A. \(\sqrt {13} .\) B. \(\sqrt 7 .\) C. \(\frac{{\sqrt {34} }}{2}.\) D. \(\frac{{\sqrt {46} }}{2}.\) Câu 18: Cho mệnh đề: “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn”. Mệnh đề đảo của mệnh đề trên là: A. “Tứ giác là một hình thoi khi và chỉ khi tứ giác đó nội tiếp được trong một đường tròn”. B. “Tứ giác là một hình thoi kéo theo tứ giác đó nội tiếp được trong một đường tròn”. C. “Một tứ giác nội tiếp được trong một đường tròn khi và chỉ khi tứ giác đó là hình thoi”. D. “Nếu một tứ giác nội tiếp được trong một đường tròn thì tứ giác đó là hình thoi”. Câu 19: Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?
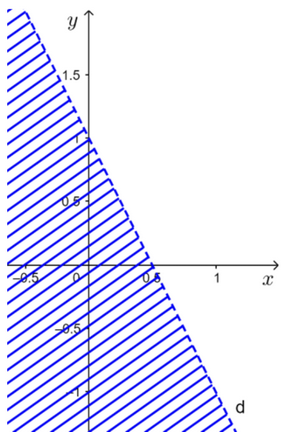
A. \(\left( {0;1} \right).\) B. \(\left( {1; + \infty } \right).\) C. \(\left[ {1; + \infty } \right).\) D. \(\left( {0;1} \right].\) Câu 20: Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. \(\sin \alpha = \sin \beta .\) B. \(\cos \alpha = - \cos \beta .\) C. \(\tan \alpha = - \tan \beta .\) D. \(\cot \alpha = \cot \beta .\) Câu 21: Cho hai tập hợp \(A = \left\{ {1;2;4;6} \right\}\) và \(B = \left\{ {1;2;3;4;5;6;7;8} \right\}\). Xác định tập hợp \({C_B}A\). A. \({C_B}A = \left\{ {3;5;7;8} \right\}.\) B. \({C_B}A = \left\{ {4;6} \right\}.\) C. \({C_B}A = \left\{ {1;2;4;6} \right\}.\) D. \({C_B}A = \left\{ {2;6;7;8} \right\}.\) Câu 22: Tam giác ABC có AB = 4, BC = 6, \(AC = 2\sqrt 7 \). Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM. A. \(AM = 3\sqrt 2 .\) B. \(AM = 4\sqrt 2 .\) C. \(AM = 2\sqrt 3 .\) D. \(AM = 3.\) Câu 23: Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
A. \(2x + y < 1.\) B. \(2x - y > 1.\) C. \(x + 2y > 1.\) D. \(2x + y > 1.\) Câu 24: Cho góc \(\alpha \) với \({0^0} < \alpha < {180^0}\). Tính giá trị của \(\cos \alpha \), biết \(\tan \alpha = - 2\sqrt 2 \). A. \( - \frac{1}{3}.\) B. \(\frac{1}{3}.\) C. \(\frac{{2\sqrt 2 }}{3}.\) D. \(\frac{{\sqrt 2 }}{3}.\) Câu 25: Một ca nô xuất phát từ cảng A, chạy theo hướng đông với vận tốc 50 km/h. Cùng lúc đó, một tàu cá, xuất phát từ A, chạy theo hướng N30°E với vận tốc 40 km/h. Sau 3 giờ, hai tàu cách nhau bao nhiêu kilômét? A. 135,7km. B. 237,5km. C. 110km. D. 137,5km. Câu 26. Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của \(\sqrt 3 \) chính xác đến hàng phần nghìn. A. 1,7320. B. 1,732. C. 1,733. D. 1,731. Câu 27. Đo độ cao một ngọn cây là \(h = 347,13{\rm{m}} \pm 0,2{\rm{m}}.\) Hãy viết số quy tròn của số gần đúng 347,13. A. 345. B. 347. C. 348. D. 346. Câu 28: Ba nhóm học sinh gồm 20 người, 15 người, 25 người. Cân nặng trung bình của mỗi nhóm lần lượt là 50kg, 38kg, 40kg. Cân nặng trung bình của cả ba nhóm học sinh là: A. 41,6kg. B. 42,8kg. C. 41,8kg. D. Đáp số khác. Câu 29: Có 100 học sinh dự thi học sinh giỏi Toán (điểm 20). Kết quả như sau:
Nhận xét nào sau đây là đúng? A. Phương sai lớn hơn 4, độ lệch chuẩn lớn hơn 2 B. Phương sai lớn hơn 5, độ lệch chuẩn lớn hơn 2 C. Phương sai nhỏ hơn 5, độ lệch chuẩn lớn hơn 2 D. Phương sai nhỏ hơn 4, độ lệch chuẩn nhỏ hơn 2 Câu 30. Cho hình chữ nhật \(ABCD.\) Khẳng định nào sau đây đúng? A. \(\overrightarrow {AC} = \overrightarrow {BD} .\) B. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \vec 0.\) C. \(\left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|.\) D. \(\left| {\overrightarrow {BC} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AC} - \overrightarrow {AB} } \right|.\) Câu 31. Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \). Mệnh đề nào sau đây sai? A. \(MABC\) là hình bình hành. B. \(\overrightarrow {AM} + \overrightarrow {AB} = \overrightarrow {AC} .\) C. \(\overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BM} .\) D. \(\overrightarrow {MA} = \overrightarrow {BC} .\) Câu 32. Cho hình bình hành ABCD. Đẳng thức nào sau đây đúng? A.\(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} \) B. \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} \) C. \(\overrightarrow {AC} - \overrightarrow {BD} = 2\overrightarrow {CD} \) D. \(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {CD} \) Câu 33. Cho tam giác OAB vuông cân tại O, cạnh \(OA = a\). Khẳng định nào sau đây sai? A.\(\left| {3\overrightarrow {OA} + 4\overrightarrow {OB} } \right| = 5a\) B. \(\left| {2\overrightarrow {OA} } \right| + \left| {3\overrightarrow {OB} } \right| = 5a\) C. \(\left| {7\overrightarrow {OA} - 2\overrightarrow {OB} } \right| = 5a\) D. \(\left| {11\overrightarrow {OA} } \right| - \left| {6\overrightarrow {OB} } \right| = 5a\) Câu 34. Cho tam giác \(ABC\) có \(BC = a,\,{\rm{ }}CA = b,{\rm{ }}AB = c.\) Gọi \(M\) là trung điểm cạnh \(BC.\) Tính \(\overrightarrow {AM} .\overrightarrow {BC} .\) A. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{b^2} - {c^2}}}{2}.\) B. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{c^2} + {b^2}}}{2}.\) C. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{c^2} + {b^2} + {a^2}}}{3}.\) D. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{c^2} + {b^2} - {a^2}}}{2}.\) Câu 35. Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} } \right).\) A. \(P = 2\sqrt 2 a.\) B. \(P = 2{a^2}.\) C. \(P = {a^2}.\) D. \(P = - 2{a^2}.\)
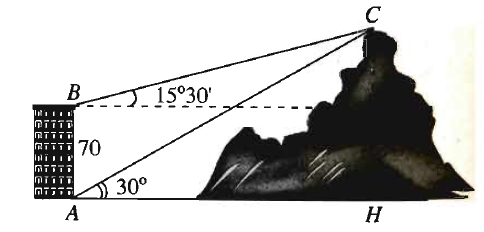
II. Tự luận (3 điểm) Câu 1: (1,5 điểm) Cho tam giác ABC, M là điểm bất kỳ. a) Chứng minh rằng \(\overrightarrow {MA} .\overrightarrow {BC} + \overrightarrow {MB} .\overrightarrow {CA} + \overrightarrow {MC} .\overrightarrow {AB} = 0\) b) Gọi G là trọng tâm tam giác ABC. Chứng minh: \(M{A^2} + M{B^2} + M{C^2} = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}\) c) Chứng minh rằng \(G{A^2} + G{B^2} + G{C^2} = \frac{1}{3}({a^2} + {b^2} + {c^2})\), với a, b, c là độ dài 3 cạnh của tam giác. Câu 2: (1 điểm) Từ hai vị trí \(A\) và \(B\) của một tòa nhà, người ta quan sát đỉnh \(C\) của ngọn núi. Biết rằng độ cao \(AB = 70{\rm{m}}\), phương nhìn \(AC\) tạo với phương nằm ngang góc \({30^0}\), phương nhìn \(BC\) tạo với phương nằm ngang góc \({15^0}30'\). Tìm độ cao của ngọn núi đó có độ cao so với mặt đất.
Câu 3: (0,5 điểm) Tính giá trị các biểu thức sau: \(P = 4\tan \left( {x + {4^0}} \right).\sin x\cot \left( {4x + {{26}^0}} \right)\) \( + \frac{{8{{\tan }^2}\left( {{3^0} - x} \right)}}{{1 + {{\tan }^2}\left( {5x + {3^0}} \right)}} + 8{\cos ^2}\left( {x - {3^0}} \right)\) khi \(x = {30^0}\)
-----HẾT----- Lời giải HƯỚNG DẪN GIẢI CHI TIẾT I. Trắc nghiệm (7 điểm)
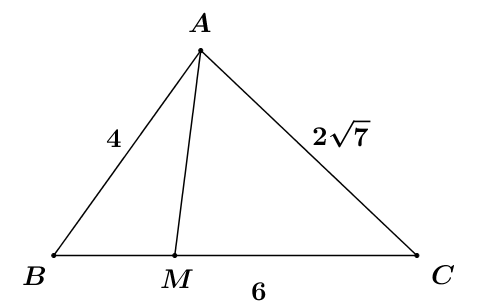
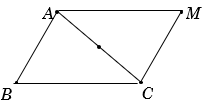
Câu 1 (NB): Phương pháp: Mệnh đề là câu khẳng định, có tính đúng hoặc sai. Cách giải: (1) và (4) là mệnh đề. Chọn B. Câu 2 (TH): Phương pháp: Phủ định của \(\forall \) là \(\exists \), phủ định của > là \( \le \). Cách giải: Mệnh đề phủ định của mệnh đề “\(\forall x \in \mathbb{R},{\kern 1pt} {\kern 1pt} x - 2 > 5\)” là “\(\exists x \in \mathbb{R},{\kern 1pt} {\kern 1pt} x - 2 \le 5\)”. Chọn A. Câu 3 (TH): Phương pháp: Viết tập hợp theo cách liệt kê các phần tử. Cách giải: Giải phương trình \(x\left( {x - 2} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\\{x = 3}\end{array}} \right.\). Mà \(x \in {\mathbb{N}^*} \Rightarrow x \in \left\{ {2;3} \right\}.\) Vậy D = {2;3}. Chọn A. Câu 4 (TH): Phương pháp: Chỉ ra các tính chất đặc trưng cho các phần tử của tập hợp B và viết tập hợp B theo cách nêu tính chất đặc trưng cho các phần tử của tập hợp. Cách giải: B = {3;6;9;12;15} \( \Rightarrow B = \left\{ {3n|n \in \mathbb{N},{\kern 1pt} {\kern 1pt} 1 \le n \le 5} \right\}\). Chọn A. Câu 5 (VD): Phương pháp: Thực hiện các phép toán trên tập hợp. Sử dụng trục số. Cách giải: +) \(A \cap B = \left( { - 3; - 2} \right]\) => A đúng. +) \(A\backslash B = \left( { - \infty ; - 3} \right]\) => B sai. +) \(A \cup B = \left( { - \infty ;5} \right]\) => C đúng. +) \(B\backslash A = \left( { - 2;5} \right]\). => D đúng. Chọn B. Câu 6 (NB): Phương pháp: Tập hợp A được gọi là tập con của tập hợp B nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B. Cách giải: \({A_3} = \left\{ {4;5} \right\} \subset A = \left\{ {1;2;3;4;5} \right\}\). Chọn C. Câu 7 (NB): Phương pháp: Tìm khẳng định đúng. Cách giải: 5 là số nguyên tố, 9, 12, 4 là hợp số nên mệnh đề D đúng. Chọn D. Câu 8 (TH): Phương pháp: Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là \(ax + by \le c\) (\(ax + by \ge c\), \(ax + by < c\), \(ax + by > c\)) Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số. Cách giải: Ta có: \(2{x^2} + 1 \ge y + 2{x^2} \Leftrightarrow y - 1 \le 0\) nên đây là một bất phương trình bậc nhất hai ẩn. Chọn C. Câu 9 (NB): Phương pháp: Thay các tọa độ điểm vào bất phương trình, điểm nào thỏa mãn bất phương trình thì thuộc miền nghiệm của bất phương trình đó. Cách giải: +) Thay tọa độ điểm (5;1) vào bất phương trình ta có: 3.5 + 2.1 < 10 (Vô lí) => (5;1) không thuộc miền nghiệm của bất phương trình. +) Thay tọa độ điểm (4;2) vào bất phương trình ta có: 3.4 + 2.2 < 10 (Vô lí) => (4;2) không thuộc miền nghiệm của bất phương trình. +) Thay tọa độ điểm (1;5) vào bất phương trình ta có: 3.1 + 2.5 < 10 (Vô lí) => (1;5) không thuộc miền nghiệm của bất phương trình. +) Thay tọa độ điểm (1;2) vào bất phương trình ta có: 3.1 + 2.2 < 10 (Đúng) => (1;2) không thuộc miền nghiệm của bất phương trình. Chọn D. Câu 10 (NB): Phương pháp: Sử dụng định lí cosin trong tam giác: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\) Cách giải: \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G\) là mệnh đề đúng. Chọn D. Câu 11 (TH): Phương pháp: Áp dụng định lí Sin trong tam giác ABC: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\). Cách giải: Áp dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\). Theo giả thiết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \Rightarrow \frac{{AC}}{{AB}} = \sqrt 3 \Rightarrow AC = \sqrt 3 AB.\) Vậy \(AC = \sqrt 3 .2\sqrt 2 = 2\sqrt 6 .\) Chọn D. Câu 12 (VD): Phương pháp: Tính sinA. Tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\) Sử dụng định lí cosin trong tam giác tính a: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\) Sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}a{h_a}\), từ đó tính \({h_a}\). Cách giải: Ta có: \(\begin{array}{*{20}{l}}{{{\sin }^2}A + {{\cos }^2}A = 1}\\{ \Leftrightarrow {{\sin }^2}A + {{\left( {\frac{3}{5}} \right)}^2} = 1}\\{ \Leftrightarrow {{\sin }^2}A = \frac{{16}}{{25}}}\end{array}\) Vì \({0^0} < A < {180^0}\) nên sinA > 0 \( \Rightarrow \sin A = \frac{4}{5}.\) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A. = \frac{1}{2}.7.5.\frac{4}{5} = 14.\) Áp dụng định lí cosin trong tam giác ABC ta có: \(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} - 2bc.\cos A.}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {7^2} + {5^2} - 2.7.5.\frac{3}{5}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 32}\\{ \Rightarrow a = 4\sqrt 2 .}\end{array}\) Lại có: \(S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}.\) Chọn C. Câu 13 (TH): Phương pháp: Với x là nghiệm của phương trình đã cho thì mệnh đề P(x) là mệnh đề đúng. Cách giải: Ta có: \({x^2} - 5x + 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 4}\end{array}} \right.\). Vậy với x = 1 thì P(x) là mệnh đề đúng. Chọn D. Câu 14 (NB): Phương pháp: Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn. Cách giải: \(\left\{ {\begin{array}{*{20}{l}}{x - 4 \ge y}\\{3x + 4y < 5}\end{array}} \right.\) là hệ bất phương trình bậc nhất hai ẩn. Chọn D. Câu 15 (NB): Phương pháp: Nhớ bảng giá trị lượng giác của các góc thường dùng hoặc sử dụng máy tính cầm tay. Cách giải: \(\begin{array}{*{20}{l}}{T = 2 + {{\sin }^2}{{90}^0} + 2{{\cos }^2}{{60}^0} - 3{{\tan }^2}{{45}^0}}\\{T = 2 + {1^2} + 2.{{\left( {\frac{1}{2}} \right)}^2} - {{3.1}^2}}\\{T = \frac{1}{2}.}\end{array}\) Chọn D. Câu 16 (NB): Phương pháp: Sử dụng các công thức tính diện tích tam giác: \({S_{ABC}} = \frac{1}{2}ab\sin C = pr = \frac{{abc}}{{4S}} = \frac{1}{2}c.{h_c}.\) Cách giải: \({S_{ABC}} = \frac{1}{2}ab\sin C\) nên đáp án A sai. Chọn A. Câu 17 (NB): Phương pháp: Áp dụng định lí Cosin trong tam giác: \(A{B^2} = B{C^2} + A{C^2} - 2BC.AC.\cos C\). Cách giải: Áp dụng định lí Cosin trong tam giác ABC: \(\begin{array}{*{20}{l}}{A{B^2} = B{C^2} + A{C^2} - 2BC.AC.\cos C}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {1^2} + {3^2} - 2.1.3.\cos {{60}^0} = 7}\\{ \Rightarrow AB = \sqrt 7 .}\end{array}\) Chọn B. Câu 18 (NB): Phương pháp: Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là \(Q \Rightarrow P\). Cách giải: Mệnh đề đảo của mệnh đề “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn” là Chọn D. Câu 19 (NB): Phương pháp: Biểu diễn tập hợp trên trục số. Cách giải: Hình vẽ đã cho là minh họa cho tập hợp \(\left[ {1; + \infty } \right).\) Chọn C. Câu 20 (NB): Phương pháp: Sử dụng mối liên hệ giá trị lượng giác của hai góc bù nhau: Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau ta có: \(\sin \alpha = \sin \beta ,\) \(\cos \alpha = - \cos \beta \), \(\tan \alpha = - \tan \beta \), \(\cot \alpha = - \cot \beta .\) Cách giải: \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau nên \(\sin \alpha = \sin \beta ,\) \(\cos \alpha = - \cos \beta \), \(\tan \alpha = - \tan \beta \), \(\cot \alpha = - \cot \beta .\) Vậy đẳng thức ở đáp án D sai. Chọn D. Câu 21 (TH): Phương pháp: \({C_B}A = B\backslash A = \{ x|x \in B\) và \(x \notin A\)}. Cách giải: Ta có: \({C_B}A = B\backslash A = \{ x|x \in B\) và \(x \notin A\)}. \( \Rightarrow {C_B}A = \left\{ {3;5;7;8} \right\}.\) Chọn A. Câu 21 (VD): Phương pháp: Sử dụng hệ quả định lí cosin trong tam giác ABC tính cosB: \(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB.BC}}\). Tính BM, CM. Sử dụng định lí cosin trong tam giác ABM tính AM: \(A{M^2} = A{B^2} + B{M^2} - 2AB.BM.\cos B\). Cách giải:
Ta có: \(\begin{array}{*{20}{l}}{\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB.BC}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{4^2} + {6^2} - {{\left( {2\sqrt 7 } \right)}^2}}}{{2.4.6}} = \frac{1}{2}}\end{array}\) Vì MC = 2MB, BC = 6 nên \(BM = \frac{1}{3}BC = \frac{1}{3}.6 = 2.\) Áp dụng định lí cosin trong tam giác ABM ta có: \(\begin{array}{*{20}{l}}{A{M^2} = A{B^2} + B{M^2} - 2AB.BM.\cos B}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {4^2} + {2^2} - 2.4.2.\frac{1}{2} = 12}\\{ \Rightarrow AM = 2\sqrt 3 .}\end{array}\) Chọn C. Câu 23 (TH): Phương pháp: Tìm phương trình đường thẳng d. Loại đáp án. Thay tọa độ điểm O(0;0) vào các bất phương trình chưa bị loại ở các đáp án, tiếp tục loại đáp án. Cách giải: Đường thẳng d đi qua điểm (0;1) nên loại đáp án B, C. Ta thấy điểm O(0;0) không thuộc miền nghiệm của bất phương trình. + Thay tọa độ điểm O(0;0) vào bất phương trình \(2x + y < 1\) ta có: 2.0 + 0 < 1 (Đúng) => Loại. + Thay tọa độ điểm O(0;0) vào bất phương trình \(2x + y > 1\) ta có: 2.0 + 0 > 1 (Vô lí) => Thỏa mãn. Chọn D. Câu 24 (TH): Phương pháp: Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}.\) Cách giải: Ta có: \(\begin{array}{*{20}{l}}{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 + {{\tan }^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}}\\{ \Leftrightarrow 1 + {{\left( { - 2\sqrt 2 } \right)}^2} = \frac{1}{{{{\cos }^2}\alpha }}}\\{ \Leftrightarrow {{\cos }^2}\alpha = \frac{1}{9}}\\{ \Leftrightarrow \cos \alpha = \pm \frac{1}{3}}\end{array}\) Vì \({0^0} < \alpha < {180^0}\) \( \Rightarrow \sin \alpha > 0\). Mà \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} < 0\) nên \(\cos \alpha < 0\). Vậy \(\cos \alpha = - \frac{1}{3}.\) Chọn A. Câu 25 (VD): Phương pháp: Hướng N300E là hướng tạo với hướng bắc một góc 300 và tạo với hướng đông một góc \({90^0} - {30^0} = {60^0}\). Áp dụng định lí cosin trong tam giác. Cách giải: Hướng N300E là hướng tạo với hướng bắc một góc 300 và tạo với hướng đông một góc \({90^0} - {30^0} = {60^0}\).
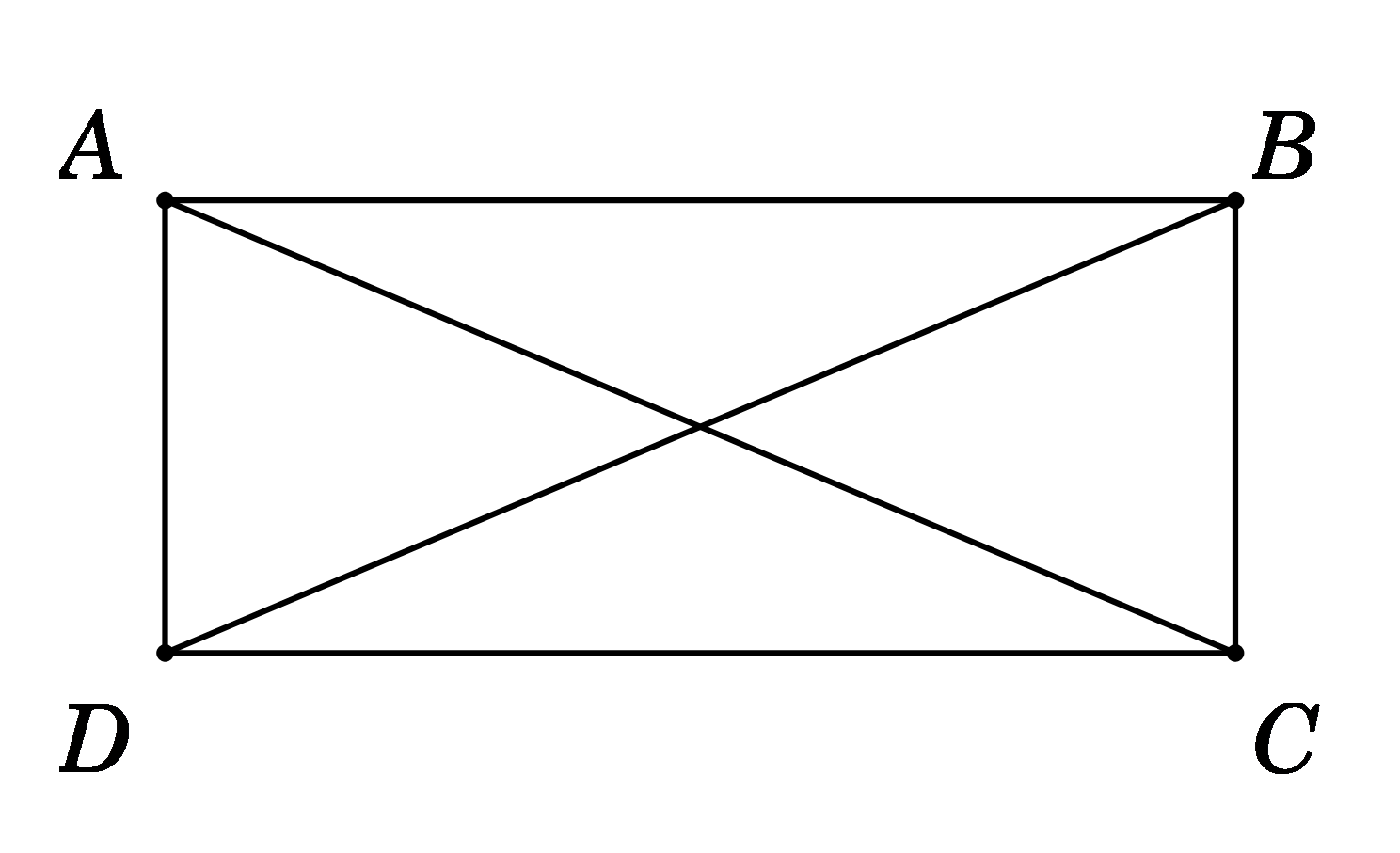
A là vị trí cảng. Ca nô đi theo hướng đông từ A đến B, sau 3 giờ đi được quãng đường AB = 50.3 = 150 (km). Tàu cá đi theo hướng N300E từ A đến C, sau 3 giờ đi được quãng đường AC = 40.3 = 120 (km). Áp dụng định lí Cosin trong tam giác ABC ta có: \(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos {{60}^{}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {{150}^2} + {{120}^2} - 2.150.120.\frac{1}{2}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 18{\kern 1pt} 900}\\{ \Rightarrow BC = 30\sqrt {21} \approx 137,5.}\end{array}\) Vậy sau 3 giờ hai tàu cách nhau khoảng 137,5km. Chọn D. Câu 26. Cách giải Sử dụng máy tính cầm tay, ta được \(\sqrt 3 = 1,7320508076...\) Làm tròn đến hàng phần nghìn ta được kết quả: $1,732$. Chọn B. Câu 27. Cách giải Ta có: \(h = 347,13{\rm{m}} \pm 0,2{\rm{m}} \Rightarrow d = 0,2\) Độ chính xác d có chữ số (khác 0) ở hàng lớn nhất là hàng phần mười, do đó ta làm tròn số gần đúng \(h = 347,13\) đến hàng đơn vị, kết quả là $347$. Chọn B Câu 28 (TH) Phương pháp: Trung bình \(\bar x = \frac{{{m_1}{x_1} + {m_2}{x_2} + ... + {m_k}{x_k}}}{n}\) trong đó mk là tần số của giá trị xk và \(n = {m_1} + {m_2} + ... + {m_k}\) Cách giải: Khối lượng trung bình của cả ba nhóm học sinh là: \(\bar x = \frac{{20.50 + 15.38 + 25.40}}{{20 + 15 + 25}} = 42,8.\) Chọn B. Câu 29 (VD): Phương pháp: Áp dụng công thức tìm phương sai và độ lệch chuẩn. Cách giải: Số trung bình cộng: \(\bar x = \frac{{9.1 + 10.1 + 11.3 + 12.5 + 13.8 + 14.13 + 15.19 + 16.24 + 17.14 + 18.10 + 19.2}}{{100}}\)\( = \frac{{1523}}{{100}} = 15,23\) (điểm) Phương sai: \({s^2} = \frac{1}{{100}}\left[ {1.{{\left( {9 - 15,23} \right)}^2} + 1.{{\left( {10 - 15,23} \right)}^2} + \; \ldots \; + 10.{{\left( {18 - 15,23} \right)}^2} + 2.{{\left( {19 - 15,23} \right)}^2}} \right]\) \( = 3,9571\)(điểm) Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)\( = \sqrt {3,9571} \; \approx 1,989{\rm{2}}\) (điểm) Vậy phương sai nhỏ hơn \(4\), độ lệch chuẩn nhỏ hơn \(2\). Chọn D. Câu 30. Cách giải:
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = BD}\\{\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC}\end{array}} \right..\) Mà \(BD = AC \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|.\) Chọn C. Câu 31. Cách giải: Ta có \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \) \( \Rightarrow MABC\) là hình bình hành \( \Rightarrow \overrightarrow {MA} = \overrightarrow {CB} .\) Do đó D sai. Chọn D. Câu 32. Cách giải: Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \) hay \(\overrightarrow {AB} + \overrightarrow {CD} = \vec 0\) Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} }\\{\overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {CD} }\end{array}} \right.\)\( \Rightarrow \overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} + \overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {BC} \) Vậy A đúng. \(\overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \) => B sai. \(\overrightarrow {AC} - \overrightarrow {BD} = \overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {DC} + \overrightarrow {DC} = 2\overrightarrow {DC} = - 2\overrightarrow {CD} \) => C sai \(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {DC} \) => D sai. Chọn A.
Câu 33. Cách giải: Ta có: \(OA = OB = a\) \( \Rightarrow \left| {2\overrightarrow {OA} } \right| + \left| {3\overrightarrow {OB} } \right| = 2a + 3a = 5a\). Vậy B đúng. Tương tự, ta có \(\left| {11\overrightarrow {OA} } \right| - \left| {6\overrightarrow {OB} } \right| = 11a - 6a = 5a\). Do đó D đúng. Lấy C, D sao cho \(\overrightarrow {OC} = 3\overrightarrow {OA} ;\overrightarrow {OD} = 4\overrightarrow {OB} ;\) Dựng hình bình hành OCED. Do \(\widehat {AOB} = {90^\circ }\) nên OCED là hình chữ nhật. Ta có: \(3\overrightarrow {OA} + 4\overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OE} \) \( \Rightarrow \left| {3\overrightarrow {OA} + 4\overrightarrow {OB} } \right| = \left| {\overrightarrow {OE} } \right| = OE\) Lại có: \(OC = 3OA = 3a,OD = 4OB = 4a.\) \( \Rightarrow OE = \sqrt {O{C^2} + C{E^2}} = \sqrt {O{C^2} + O{D^2}} = \sqrt {{{(3a)}^2} + {{(4a)}^2}} = 5a\) Do đó A đúng. Chọn C Câu 34. Cách giải: Vì M là trung điểm của BC suy ra \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) Khi đó \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\) \( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right) = \frac{{{b^2} - {c^2}}}{2}\) Chọn A. Câu 35. Cách giải: Ta có \(\left\{ \begin{array}{l}BD = a\sqrt 2 \\\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} = \left( {\overrightarrow {BC} + \overrightarrow {BA} } \right) + \overrightarrow {BD} = \overrightarrow {BD} + \overrightarrow {BD} = 2\overrightarrow {BD} \end{array} \right.\) Khi đó \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).2\overrightarrow {BD} = 2\overrightarrow {AB} .\overrightarrow {BD} + 2\overrightarrow {AC} .\overrightarrow {BD} = - 2\overrightarrow {BA} .\overrightarrow {BD} + \vec 0\) \( = - 2BA.BD\cos \left( {\overrightarrow {BA} ,\overrightarrow {BD} } \right) = - 2.a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = - 2{a^2}\) Chọn D.
II. Tự luận (3 điểm) Câu 1 (TH): Cách giải: a) Ta có: \( = \overrightarrow {{\rm{MA}}} \cdot (\overrightarrow {{\rm{MC}}} - \overrightarrow {{\rm{MB}}} ) + \overrightarrow {{\rm{MB}}} (\overrightarrow {{\rm{MA}}} - \overrightarrow {{\rm{MC}}} ) + \overrightarrow {{\rm{MC}}} (\overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MA}}} ) = \) \( = \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MC}}} - \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MA}}} - \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MA}}} \) \( = \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MC}}} - \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MA}}} - \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MA}}} - \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MB}}} = 0\) b) \({\rm{M}}{{\rm{A}}^2} = {\overrightarrow {{\rm{MA}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GA}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GA}}} \) \({\rm{M}}{{\rm{B}}^2} = {\overrightarrow {{\rm{MB}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GB}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{B}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GB}}} \) \({\rm{M}}{{\rm{C}}^2} = {\overrightarrow {{\rm{MC}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GC}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{C}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GC}}} \) \( \Rightarrow {\rm{M}}{{\rm{A}}^2} + {\rm{M}}{{\rm{B}}^2} + {\rm{M}}{{\rm{C}}^2} = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} + 2(\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GA}}} + \overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GB}}} + \overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GC}}} )\) \( = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} + 2\overrightarrow {{\rm{MG}}} (\overrightarrow {{\rm{GA}}} + \overrightarrow {{\rm{GB}}} + \overrightarrow {{\rm{GC}}} ) = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\) c) Vì \({\rm{M}}{{\rm{A}}^2} + {\rm{M}}{{\rm{B}}^2} + {\rm{M}}{{\rm{C}}^2} = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\) đúng với M bất kì. Chọn \({\rm{M}} \equiv {\rm{A}}\) ta được: \({\rm{A}}{{\rm{A}}^2} + {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 3{\rm{A}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\) \( \Leftrightarrow {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 4{\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\) Tương tự, \({\rm{M}} \equiv {\rm{B}} \Rightarrow {\rm{B}}{{\rm{A}}^2} + {\rm{B}}{{\rm{C}}^2} = 4\;{\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{C}}^2}\) \({\rm{M}} \equiv {\rm{C}} \Rightarrow {\rm{C}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 4{\rm{G}}{{\rm{C}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{A}}^2}\) Thay \(AB = c,AC = b,BC = a\) \(\begin{array}{*{20}{l}}{ \Rightarrow 6\left( {{\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}} \right) = 2\left( {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \right)}\\{ \Leftrightarrow {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} = \frac{1}{3}\left( {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \right)}\end{array}\) Câu 2 (VD): Cách giải: Từ giả thiết, ta suy ra tam giác ABC có \(\widehat {CAB} = {60^\circ },\widehat {ABC} = {105^\circ }30'\) và \(c = 70\) Khi đó \(\widehat A + \widehat B + \widehat C = {180^\circ } \Leftrightarrow \widehat C = {180^\circ } - \left( {\widehat A + \widehat B} \right) = {180^\circ } - {165^\circ }30' = {14^\circ }30'\) Theo định lí sin, ta có \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\) hay \(\frac{b}{{\sin {{105}^\circ }30'}} = \frac{{70}}{{\sin {{14}^\circ }30'}}\) Do đó \(AC = b = \sin {105^\circ }30'\frac{{70}}{{\sin {{14}^\circ }30'}} \approx 269,4m\) Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc \({30^\circ }\) nên \(CH = \frac{{AC}}{2} = \frac{{269,4}}{2} = 134,7m\) Vậy ngọn núi cao khoảng 135m. Câu 3 (VDC): Phương pháp: Thay \(x = {30^0}\), sử dụng mối quan hệ giá trị lượng giác của hai góc bù nhau. Cách giải: Thay \(x = {30^0}\) ta có: \(\begin{array}{*{20}{l}}{P = 4\tan \left( {{{30}^0} + {4^0}} \right).\sin {{30}^0}\cot \left( {{{4.30}^0} + {{26}^0}} \right) + \frac{{8{{\tan }^2}\left( {{3^0} - {{30}^0}} \right)}}{{1 + {{\tan }^2}\left( {{{5.30}^0} + {3^0}} \right)}} + 8{{\cos }^2}\left( {{{30}^0} - {3^0}} \right)}\\{P = 4\tan {{34}^0}.\sin {{30}^0}\cot {{146}^0} + \frac{{8{{\tan }^2}\left( { - {{27}^0}} \right)}}{{1 + {{\tan }^2}{{153}^0}}} + 8{{\cos }^2}{{27}^0}}\\{P = 4\tan {{34}^0}.\sin {{30}^0}\cot \left( {{{180}^0} - {{34}^0}} \right) + 8{{\tan }^2}{{27}^0}{{\cos }^2}{{153}^0} + 8{{\cos }^2}{{27}^0}}\\{P = - 4\tan {{34}^0}.\sin {{30}^0}\cot {{34}^0} + 8{{\tan }^2}{{27}^0}{{\cos }^2}\left( {{{180}^0} - {{27}^0}} \right) + 8{{\cos }^2}{{27}^0}}\\{P = - 4.\sin {{30}^0} + 8{{\tan }^2}{{27}^0}{{\cos }^2}{{27}^0} + 8{{\cos }^2}{{27}^0}}\\{P = - 4.\sin {{30}^0} + 8{{\cos }^2}{{27}^0}\left( {{{\tan }^2}{{27}^0} + 1} \right)}\\{P = - 4.\sin {{30}^0} + 8{{\cos }^2}{{27}^0}\frac{1}{{{{\cos }^2}{{27}^0}}}}\\{P = - 4.\frac{1}{2} + 8}\\{P = 6}\end{array}\)
|














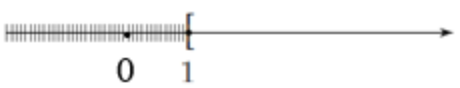

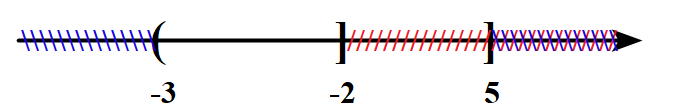

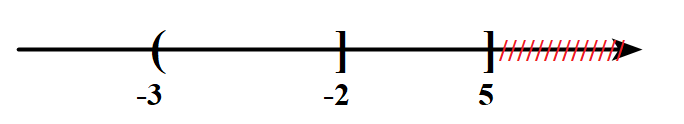
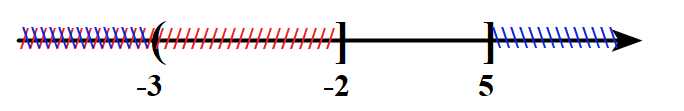







Danh sách bình luận