Đề thi, đề kiểm tra Toán lớp 10 - Kết nối tri thức

Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 14

Tải về

Làm đề thi

Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 14

Đề bài

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1 :

Phủ định của mệnh đề: “$\forall x \in {\mathbb{R}}:x^{2} + 1 > 0$” là

A

“$\forall x \in {\mathbb{R}}:x^{2} + 1 = 0$”.
B

“$\exists x \in {\mathbb{R}}:x^{2} + 1 \leq 0$”.
C

“$\exists x \in {\mathbb{R}}:x^{2} + 1 > 0$”.
D

“$\forall x \in {\mathbb{R}}:x^{2} + 1 < 0$”.

Câu 2 :

Cho hai tập hợp A và B. Sơ đồ ven phần bị gạch dưới đây mô tả phép tập hợp nào?

A

$C_{A}B$.
B

$A\backslash B$.
C

$A \cup B$.
D

$A \cap B$.

Câu 3 :

Cho hệ phương trình $\left\{ \begin{array}{l} {x + 3y - 2 \geq 0} \\ {2x + y + 1 \leq 0} \end{array} \right.$. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?

A

$N\,\left( {- 1\,;\, 1} \right)$.
B

$M\,\left( {0\,;\, 1} \right)$.
C

$P\,\left( {1\,;\, 3} \right)$.
D

$Q\,\left( {- 1\,;\, 0} \right)$.

Câu 4 :

Bạn Hoa tiết kiệm được 420 nghìn đồng. Trong đợt ủng hộ đồng bào bị lũ lụt thiệt hại do bão Yagi vừa qua, Hoa đã ủng hộ $x$ tờ tiền loại 10 nghìn đồng và $y$ tờ tiền loại 20 nghìn đồng. Bất phương trình nào dưới đây thể hiện số tờ tiền 10 nghìn và 20 nghìn mà bạn Hoa có thể ủng hộ.

A

$x + \text{2}y < \text{4}2\text{0}$.
B

$x + \text{2}y \leq \text{4}2\text{0}$.
C

$x + \text{2}y \leq \text{4}2$.
D

$x + \text{2}y \geq \text{4}2$.

Câu 5 :

Cho $\triangle ABC$ có $\widehat{B} = 60^o$, $BC = 8$, $AB = 5$. Độ dài cạnh $AC$ bằng

A

129.
B

49.
C

7.
D

$\sqrt{129}$.

Câu 6 :

Cho tam giác ABC có a = 4, b = 6, c = 8 Khi đó diện tích tam giác bằng

A

$3\sqrt{15}$.
B

$9\sqrt{15}$.
C

$2\sqrt{15}$.
D

$\dfrac{2\sqrt{15}}{3}$.

Câu 7 :

Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ $\overset{\rightarrow}{a},\overset{\rightarrow}{b},\overset{\rightarrow}{c}$ (hình vẽ). Chọn khẳng định sai trong các khẳng định sau.

A

$\overset{\rightarrow}{c}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng phương.
B

$\overset{\rightarrow}{c}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng hướng.
C

$\overset{\rightarrow}{a}$ và $\overset{\rightarrow}{c}$ là hai vectơ cùng hướng.
D

$\overset{\rightarrow}{a}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng phương.

Câu 8 :

Rút gọn biểu thức $\overset{\rightarrow}{AB} - \overset{\rightarrow}{MB} + \overset{\rightarrow}{MC} + \overset{\rightarrow}{CD} - \overset{\rightarrow}{ED}$ có kết quả là:

A

$\overset{\rightarrow}{AC}$.
B

$\overset{\rightarrow}{AE}$.
C

$\overset{\rightarrow}{AD}$.
D

$\overset{\rightarrow}{AM}$.

Câu 9 :

Trong hệ tọa độ Oxy, cho A(2; -3), B(4; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB

A

$I\left( {3;\ 2} \right)$.
B

$I\left( 6;-2 \right)$.
C

$I\left(3;4\right)$.
D

$I\left( {8;- 21} \right)$.

Câu 10 :

Trong hệ tọa độ $Oxy$, cho $\overset{\rightarrow}{u} = \overset{\rightarrow}{i} + 3\overset{\rightarrow}{j}$ và $\overset{\rightarrow}{v} = \left( {2; - 1} \right)$. Tính $\overset{\rightarrow}{u}.\overset{\rightarrow}{v}$.

A

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = - 1$.
B

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = \left( {2; - 3} \right)$.
C

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = 5\sqrt{2}$.
D

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = 1$.

Câu 11 :

Cho giá trị gần đúng của $\dfrac{8}{17}$ là 0,47. Sai số tuyệt đối của 0,47 là

A

0,002.
B

0,003.
C

0,001.
D

0,004.

Câu 12 :

Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày:

9 8 22 20 18 15 19 13 11

Số ghế trống trung bình trong 9 ngày của rạp chiếu phim trên là

A

22.
B

18.
C

15.
D

135.

Phần II: Câu trắc nghiệm đúng sai.

Thí sinh trả lời câu 1, câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1 :

Trong mặt phẳng tọa độ Oxy, cho ba vecto $\overrightarrow a = (1;2)$, $\overrightarrow b = ( - 3;1)$, $\overrightarrow c = ( - 3;4)$.

a) a, b là hai vecto cùng phương.

Đúng

Sai

b) $2\overrightarrow a = (2;4)$.

Đúng

Sai

c) $\overrightarrow a + 2\overrightarrow b - 3\overrightarrow c = (4; - 12)$.

Đúng

Sai

d) $\overrightarrow c = m.\overrightarrow a + n.\overrightarrow b$ và $m + n = \frac{{19}}{7}$.

Đúng

Sai

Câu 2 :

Nhiệt độ trung bình các tháng trong một năm gần đây của tỉnh Bắc Ninh được cho bởi bảng thống kê bên dưới (đơn vị: độ C, nguồn: https://vi.weatherspark.com/):

17, 18, 21, 24, 27, 29, 29, 28, 25, 22, 18.

a) Một của mẫu số liệu trên là 29.

Đúng

Sai

b) Khoảng biến thiên của mẫu số liệu trên là 9.

Đúng

Sai

c) Số trung bình của mẫu số liệu đã cho bằng 23,92.

Đúng

Sai

d) Số trung vị của mẫu số liệu đã là 24,5.

Đúng

Sai

Phần III: Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1 :

Cho tập hợp $A = \left\{ {x \in \mathbb{R}|\left( {\frac{6}{5}x - 31} \right)\left( {{x^2} + 1} \right) \le 0} \right\}$. Khi đó, tập hợp $A \cap \mathbb{N}$ có tất cả bao nhiêu phần tử?

Câu 2 :

Một cột điện cao 20 m được dựng thẳng trên một triền dốc nghiêng hợp với phương ngang một góc $17^o$, đáy cột nằm theo phương ngang với điểm cuối dốc. Người ta nối một dây cáp từ đỉnh cột điện đến cuối dốc. Tìm chiều dài của dây cáp biết rằng đoạn đường từ đáy cột đến cuối dốc bằng 72 m. (Kết quả làm tròn đến hàng phần mười).

Câu 3 :

Một công ty, trong một tháng cần sản xuất ít nhất 12 viên kim cương to và 9 viên kim cương nhỏ. Từ một tấn cacbon loại 1 (giá 100 triệu đồng) có thể chiết xuất được 5 viên kim cương to và 3 viên kim cương nhỏ, từ một tấn cacbon loại 2 (giá 40 triệu đồng) có thể chiết xuất được 2 viên kim cương to và 3 viên kim cương nhỏ. Mỗi viên kim cương to giá 20 triệu đồng, mỗi viên kim cương nhỏ giá 10 triệu đồng. Hỏi mỗi tháng công ty lãi được nhiều nhất bao nhiêu triệu đồng? Biết mỗi tháng chỉ sử dụng tối đa 4 tấn cacbon mỗi loại và tổng số tiền mua cacbon không vượt quá 500 triệu đồng.

Câu 4 :

Cho ba lực $\overrightarrow {{F_1}} = \overrightarrow {MA} $, $\overrightarrow {{F_2}} = \overrightarrow {MB} $, $\overrightarrow {{F_3}} = \overrightarrow {MC} $ cùng tác động vào một vật tại điểm M và vật đứng yên (tham khảo hình vẽ). Cho biết cường độ của $\overrightarrow {{F_1}} $, $\overrightarrow {{F_2}} $ đều bằng $100\sqrt 2 $ N và góc $\widehat {AMB} = {90^o}$. Tính cường độ của lực $\overrightarrow {{F_3}} $ (đơn vị N).

Phần IV: Tự luận.

Thí sinh trình bày lời giải từ câu 1 đến câu 3.

Câu 1 :

Cho bốn điểm A, B, C, D. Chứng minh $\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0$ (*).

Câu 2 :

a) Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(1; -2), B(0; 4), C(3; 2). Tìm tọa độ điểm N sao cho $\overset{\rightarrow}{AN} + 2\overset{\rightarrow}{BN} - 4\overset{\rightarrow}{CN} = \overset{\rightarrow}{0}$.

b) Một máy bay đang bay từ hướng Đông sang hướng Tây với vận tốc 750 km/h thì gặp luồng gió thổi từ hướng Đông Bắc sang hướng Tây Nam với vận tốc 40 km/h (hình vẽ dưới). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Hãy tìm vận tốc mới của máy bay (làm tròn kết quả đến hàng phần chục theo đơn vị km/h).

$D:\THÚY HẰNG 2023\SÁCH MỚI 2022\KẾT NỐI\CK1-2024-2025 3 KHỐI 3 BỘ SÁCH\MỚI\z6099046981637_fa96cf44cd8bbf6b9753e62e75d5cc60.jpg$

Câu 3 :

Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:

Ngày	22	23	24	25	26	27	28	29	30	31
Nhiệt độ (độ C)	23	25	26	27	27	27	27	21	19	18

a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.

b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải và đáp án

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1 :

Phủ định của mệnh đề: “$\forall x \in {\mathbb{R}}:x^{2} + 1 > 0$” là

A

“$\forall x \in {\mathbb{R}}:x^{2} + 1 = 0$”.
B

“$\exists x \in {\mathbb{R}}:x^{2} + 1 \leq 0$”.
C

“$\exists x \in {\mathbb{R}}:x^{2} + 1 > 0$”.
D

“$\forall x \in {\mathbb{R}}:x^{2} + 1 < 0$”.

Đáp án : B

Phương pháp giải :

Phủ định của mệnh đề “$\forall x \in \mathbb{R}:$ A” là “$\exists x \in \mathbb{R}:$ Không phải A”.

Lời giải chi tiết :

Phủ định của mệnh đề “$\forall x \in \mathbb{R}:{x^2} + 1 > 0$” là “$\exists x \in \mathbb{R}:{x^2} + 1 \le 0$”.

Câu 2 :

Cho hai tập hợp A và B. Sơ đồ ven phần bị gạch dưới đây mô tả phép tập hợp nào?

A

$C_{A}B$.
B

$A\backslash B$.
C

$A \cup B$.
D

$A \cap B$.

Đáp án : C

Phương pháp giải :

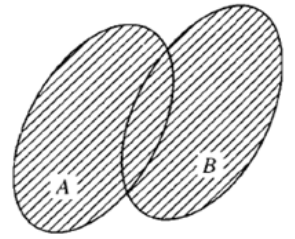
Áp dụng lý thuyết về hợp, giao, phần bù, hiêu của hai tập hợp.

Lời giải chi tiết :

Sơ đồ Ven phần bị gạch mô tả tập hợp $A \cup B$.

Câu 3 :

A

$N\,\left( {- 1\,;\, 1} \right)$.
B

$M\,\left( {0\,;\, 1} \right)$.
C

$P\,\left( {1\,;\, 3} \right)$.
D

$Q\,\left( {- 1\,;\, 0} \right)$.

Đáp án : A

Phương pháp giải :

Thay tọa độ từng điểm vào hệ đã cho, nếu thỏa mãn thì điểm đó thuộc miền nghiệm của hệ đó.

Lời giải chi tiết :

Ta thấy $\left\{ \begin{array}{l} - 1 + 3.1 - 2 = 0 \ge 0\\2.( - 1) + 1 + 1 = 0 \le 0\end{array} \right.$ (thỏa mãn) nên N(-1;1) thuộc miền nghiệm của hệ.

Câu 4 :

A

$x + \text{2}y < \text{4}2\text{0}$.
B

$x + \text{2}y \leq \text{4}2\text{0}$.
C

$x + \text{2}y \leq \text{4}2$.
D

$x + \text{2}y \geq \text{4}2$.

Đáp án : C

Phương pháp giải :

Lập bất phương trình thể hiện số tiền Hoa ủng hộ dựa theo giả thiết.

Lời giải chi tiết :

Với x tờ 10 nghìn đồng, Hoa ủng hộ được 10x nghìn đồng.

Với y tờ 20 nghìn đồng, Hoa ủng hộ được 20y nghìn đồng.

Vì Hoa tiết kiệm được 420 nghìn đồng nên số tiền ủng hộ không vượt quá 420 nghìn đồng.

Do đó, ta có bất phương trình $10x + 20y \le 420$ hay $x + 2y \le 42$.

Câu 5 :

Cho $\triangle ABC$ có $\widehat{B} = 60^o$, $BC = 8$, $AB = 5$. Độ dài cạnh $AC$ bằng

A

129.
B

49.
C

7.
D

$\sqrt{129}$.

Đáp án : C

Phương pháp giải :

Áp dụng định lí cosin: $AC = \sqrt {A{B^2} + B{C^2} - 2AB.BC.\cos ABC} $.

Lời giải chi tiết :

$AC = \sqrt {A{B^2} + B{C^2} - 2AB.BC.\cos ABC} $

$ = \sqrt {{5^2} + {8^2} - 2.5.8.\cos {{60}^o}} = 7$.

Câu 6 :

Cho tam giác ABC có a = 4, b = 6, c = 8 Khi đó diện tích tam giác bằng

A

$3\sqrt{15}$.
B

$9\sqrt{15}$.
C

$2\sqrt{15}$.
D

$\dfrac{2\sqrt{15}}{3}$.

Đáp án : A

Phương pháp giải :

Áp dụng công thức Heron: $S = \sqrt {p(p - a)(p - b)(p - c)} $.

Lời giải chi tiết :

$p = \frac{{a + b + c}}{2} = \frac{{4 + 6 + 8}}{2} = 9$.

$S = \sqrt {p(p - a)(p - b)(p - c)}$

$ = \sqrt {9(9 - 4)(9 - 6)(9 - 8)} = 3\sqrt {15} $.

Câu 7 :

A

$\overset{\rightarrow}{c}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng phương.
B

$\overset{\rightarrow}{c}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng hướng.
C

$\overset{\rightarrow}{a}$ và $\overset{\rightarrow}{c}$ là hai vectơ cùng hướng.
D

$\overset{\rightarrow}{a}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng phương.

Đáp án : B

Phương pháp giải :

Quan sát hình vẽ và trả lời.

Lời giải chi tiết :

$\overset{\rightarrow}{c}$ và $\overset{\rightarrow}{b}$ là hai vectơ ngược hướng nên mệnh đề ở đáp án B sai.

Câu 8 :

Rút gọn biểu thức $\overset{\rightarrow}{AB} - \overset{\rightarrow}{MB} + \overset{\rightarrow}{MC} + \overset{\rightarrow}{CD} - \overset{\rightarrow}{ED}$ có kết quả là:

A

$\overset{\rightarrow}{AC}$.
B

$\overset{\rightarrow}{AE}$.
C

$\overset{\rightarrow}{AD}$.
D

$\overset{\rightarrow}{AM}$.

Đáp án : B

Phương pháp giải :

Áp dụng quy tắc ba điểm.

Lời giải chi tiết :

$\overrightarrow {AB} - \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {CD} - \overrightarrow {ED} = \overrightarrow {AB} + \overrightarrow {BM} + \overrightarrow {MC} + \overrightarrow {CD} + \overrightarrow {DE} = \overrightarrow {AE} $.

Câu 9 :

Trong hệ tọa độ Oxy, cho A(2; -3), B(4; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB

A

$I\left( {3;\ 2} \right)$.
B

$I\left( 6;-2 \right)$.
C

$I\left(3;4\right)$.
D

$I\left( {8;- 21} \right)$.

Đáp án : A

Phương pháp giải :

$I = \left( {\frac{{x_A + x_B}}{2};\frac{{ y_A + y_B}}{2}} \right) $.

Lời giải chi tiết :

I là trung điểm của AB thì $I = \left( {\frac{{x_A + x_B}}{2};\frac{{ y_A + y_B}}{2}} \right) $.

Câu 10 :

A

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = - 1$.
B

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = \left( {2; - 3} \right)$.
C

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = 5\sqrt{2}$.
D

$\overset{\rightarrow}{u}.\overset{\rightarrow}{v} = 1$.

Đáp án : A

Phương pháp giải :

Áp dụng biểu thức tọa độ tích vô hướng của hai vecto.

Lời giải chi tiết :

$\overrightarrow u = (1;3)$, $\overrightarrow v = (2; - 1)$.

$\overrightarrow u .\overrightarrow v = 1.2 + 3.( - 1) = - 1$.

Câu 11 :

Cho giá trị gần đúng của $\dfrac{8}{17}$ là 0,47. Sai số tuyệt đối của 0,47 là

A

0,002.
B

0,003.
C

0,001.
D

0,004.

Đáp án : C

Phương pháp giải :

Áp dụng công thức ${\Delta _a} = \left| {\overline a - a} \right|$.

Lời giải chi tiết :

${\Delta _a} = \left| {\frac{8}{{17}} - 0,47} \right| \approx 0,0006 \approx 0,001$.

Câu 12 :

Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày:

9 8 22 20 18 15 19 13 11

Số ghế trống trung bình trong 9 ngày của rạp chiếu phim trên là

A

22.
B

18.
C

15.
D

135.

Đáp án : C

Phương pháp giải :

Áp dụng công thức: $\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}$.

Lời giải chi tiết :

Số ghế trống trung bình trong 9 ngày của rạp là:

$\overline x = \frac{{9 + 8 + 22 + 20 + 18 + 15 + 19 + 13 + 11}}{9} = 15$.

Phần II: Câu trắc nghiệm đúng sai.

Thí sinh trả lời câu 1, câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1 :

Trong mặt phẳng tọa độ Oxy, cho ba vecto $\overrightarrow a = (1;2)$, $\overrightarrow b = ( - 3;1)$, $\overrightarrow c = ( - 3;4)$.

a) a, b là hai vecto cùng phương.

Đúng

Sai

b) $2\overrightarrow a = (2;4)$.

Đúng

Sai

c) $\overrightarrow a + 2\overrightarrow b - 3\overrightarrow c = (4; - 12)$.

Đúng

Sai

d) $\overrightarrow c = m.\overrightarrow a + n.\overrightarrow b$ và $m + n = \frac{{19}}{7}$.

Đúng

Sai

Đáp án

a) a, b là hai vecto cùng phương.

Đúng

Sai

b) $2\overrightarrow a = (2;4)$.

Đúng

Sai

c) $\overrightarrow a + 2\overrightarrow b - 3\overrightarrow c = (4; - 12)$.

Đúng

Sai

d) $\overrightarrow c = m.\overrightarrow a + n.\overrightarrow b$ và $m + n = \frac{{19}}{7}$.

Đúng

Sai

Phương pháp giải :

Áp dụng biểu thức tọa độ của các phép toán vecto.

Lời giải chi tiết :

a) Sai. $\frac{1}{{ - 3}} \ne \frac{2}{1}$ nên a, b là hai vecto không cùng phương.

b) Đúng. $2a = (2.1;2.2) = (2;4)$.

c) Sai. $a + 2b - 3c = (4; - 8)$.

d) Đúng. $\overrightarrow c = m\overrightarrow a + n\overrightarrow b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m - 3n = - 3}\\{2m + n = 4}\end{array}} \right.$

$\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m = \frac{9}{7}}\\{n = \frac{{10}}{7}}\end{array}} \right. \Rightarrow m + n = \frac{{19}}{7}$.

Câu 2 :

17, 18, 21, 24, 27, 29, 29, 28, 25, 22, 18.

a) Một của mẫu số liệu trên là 29.

Đúng

Sai

b) Khoảng biến thiên của mẫu số liệu trên là 9.

Đúng

Sai

c) Số trung bình của mẫu số liệu đã cho bằng 23,92.

Đúng

Sai

d) Số trung vị của mẫu số liệu đã là 24,5.

Đúng

Sai

Đáp án

a) Một của mẫu số liệu trên là 29.

Đúng

Sai

b) Khoảng biến thiên của mẫu số liệu trên là 9.

Đúng

Sai

c) Số trung bình của mẫu số liệu đã cho bằng 23,92.

Đúng

Sai

d) Số trung vị của mẫu số liệu đã là 24,5.

Đúng

Sai

Phương pháp giải :

a) Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất, kí hiệu: ${M_o}$.

b) Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.

c) Số trung bình (hay TB cộng) của mẫu số liệu kí hiệu là $\overline x $, được tính bằng công thức: $\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}$.

d) Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm (hoặc không tăng).

- Nếu n là số lẻ thì số liệu đứng ở vị trí thứ $\frac{n+1}{2}$ (số đứng chính giữa) gọi là trung vị.

- Nếu n là số chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ $\frac{n}{2}$ và $\frac{n}{2}+1$ gọi là trung vị.

Lời giải chi tiết :

a) Đúng. Vì số 29 xuất hiện nhiều nhất trong mẫu số liệu nên mốt của mẫu số liệu là 29.

b) Sai. Khoảng biến thiên của mẫu số liệu là 29 - 17 = 12.

c) Đúng. Số trung bình của mẫu số liệu là $x = \frac{17 + 18 + 21 + 24 + 27 + 29 + 29 + 28 + 25 + 22 + 18}{12} \approx 23,92$.

d) Đúng. Sắp xếp mẫu số liệu theo thứ tự không giảm:

17, 18, 18, 21, 22, 24, 25, 27, 28, 29, 29, 29.

Trung vị của mẫu số liệu là $\frac{1}{2}(24 + 25) = 24,5$.

Phần III: Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1 :

Phương pháp giải :

Giải bất phương trình rồi tìm giao (phần chung) của hai tập hợp.

Lời giải chi tiết :

Đáp án :

Do ${x^2} + 1 > 0$, $\forall x \in \mathbb{R}$ nên bất phương trình: $\left( {\frac{6}{5}x - 31} \right)\left( {{x^2} + 1} \right) \le 0 \Leftrightarrow \frac{6}{5}x - 31 \le 0 \Leftrightarrow x \le \frac{{155}}{6}$.

Do đó $A = \left( { - \infty ;\frac{{155}}{6}} \right] \Rightarrow A \cap \mathbb{N} = \left\{ {0;1;2;...;25} \right\}$.

Vậy $A \cap \mathbb{N}$ có 26 phần tử.

Câu 2 :

Phương pháp giải :

Áp dụng định lí cosin.

Lời giải chi tiết :

Đáp án :

Ta coi đáy cọc là điểm B, chân dốc là điểm A, cột điện được chôn tại điểm C như hình vẽ dưới đây.

Ta có $\widehat{ACD} = 90^o + 17^o = 107^o$.

Trong tam giác ABC vuông tại B có $AC = \frac{AB}{\cos 17^o} \approx 75,3$ m.

Áp dụng định lý cosin trong tam giác $ACD$, ta có:

$AD^2 = AC^2 + CD^2 - 2 . AC . CD . \cos ACD $

$\approx 75,3^2 + 20^2 - 2 . 75,3 . 20 . \cos 107^o \approx 6950,7$.

$\Rightarrow AD \approx 83,4$ (m).

Câu 3 :

Phương pháp giải :

Ứng dụng hệ bất phương trình bậc nhất hai ẩn để giải.

Lời giải chi tiết :

Đáp án :

Gọi x, y (tấn) lần lượt là số tấn cacbon loại 1 và loại 2 sử dụng mỗi tháng,

Số viên kim cương loại to là 5x + 2y.

Số viên kim cương loại nhỏ là 3x + 3y.

Tổng số tiền mua cacbon là 100x + 40y.

Số tiền thu vào từ bán kim cương là 20(5x + 2y) + 10(3x + 3y) = 130x + 70y.

Ta có hệ bất phương trình: $\left\{ {\begin{array}{*{20}{l}}{x,y \ge 0}\\{x \le 4}\\{y \le 4}\\{100x + 40y \le 500}\\{5x + 2y \ge 12}\\{3x + 3y \ge 9}\end{array}} \right.$

Miền nghiệm của bất phương trình là ngũ giác ABCDEG, trong đó tọa độ các đỉnh là A(3; 0), B(2; 1), $C\left( {\frac{4}{5};4} \right)$, $D\left( {\frac{{17}}{5};4} \right)$, $E\left( {4;\frac{5}{2}} \right)$, G(4; 0).

Số tiền lãi mỗi tháng là f(x; y) = 30x + 30y.

Tại điểm $D\left( {\frac{{17}}{5};4} \right)$ ta có $f\left( {\frac{{17}}{5};4} \right) = 222$ là giá trị lớn nhất. Vậy mỗi tháng công ty lãi nhiều nhất là 222 triệu đồng.

Câu 4 :

Phương pháp giải :

Áp dụng quy tắc hình bình hành.

Lời giải chi tiết :

Đáp án :

Gọi D là điểm để tứ giác MADB là hình vuông.

Theo bài ra ta có $\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| $

$= \left| {\overrightarrow {MD} } \right| = 100\sqrt 2 .\sqrt 2 = 200$ N.

Phần IV: Tự luận.

Thí sinh trình bày lời giải từ câu 1 đến câu 3.

Câu 1 :

Cho bốn điểm A, B, C, D. Chứng minh $\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0$ (*).

Phương pháp giải :

Tách vectơ và đưa về các vectơ chung gốc (gốc A).

Lời giải chi tiết :

Biến đổi vế trái (*) ta có:

$\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} $

$= \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) + \overrightarrow {AC} .\left( {\overrightarrow {AB} - \overrightarrow {AD} } \right) + \overrightarrow {AD} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)$

$ = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AC} - \overrightarrow {AC} .\overrightarrow {AD} + \overrightarrow {AC} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AD} = 0$ = VP (*) (ĐPCM)

Câu 2 :

$D:\THÚY HẰNG 2023\SÁCH MỚI 2022\KẾT NỐI\CK1-2024-2025 3 KHỐI 3 BỘ SÁCH\MỚI\z6099046981637_fa96cf44cd8bbf6b9753e62e75d5cc60.jpg$

Phương pháp giải :

Áp dụng các phép toán vecto trên mặt phẳng tọa độ.

Lời giải chi tiết :

a) $ \Leftrightarrow ({x_N} - 1;{y_N} + 2) + 2({x_N};{y_N} - 4) - 4({x_N} - 3;{y_N} - 2) = (0;0)$ $ \Leftrightarrow ( - {x_N} + 11; - {y_N} + 2) = (0;0) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_N} = 11}\\{{y_N} = 2}\end{array}} \right. \Leftrightarrow N(11;2)$.

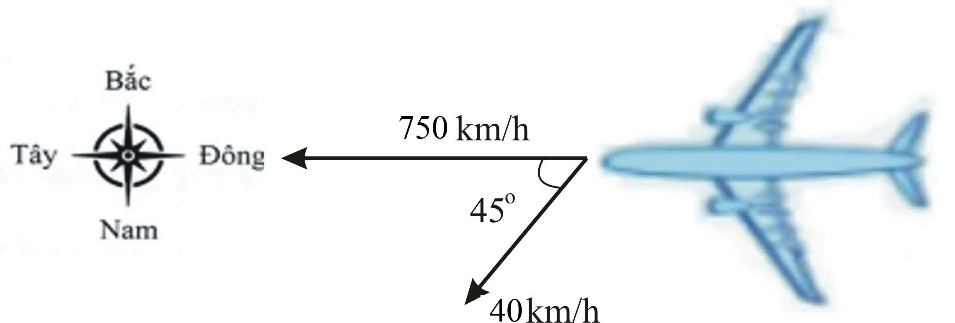
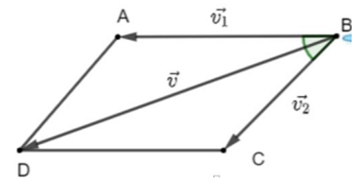
Gọi $\overrightarrow {{v_1}} $ là vận tốc của máy bay khi chưa có gió, $\left| {\overrightarrow {{v_1}} } \right| = 750$ (km/h); $\overrightarrow {{v_2}} $ là vận tốc của gió, $\left| {\overrightarrow {{v_2}} } \right| = 40$ (km/h); $\overrightarrow v$ là vận tốc của máy bay khi gặp gió.

Ta có: $\overrightarrow v = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} $ và $(\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} ) = {45^o}$.

${\overrightarrow v^2} = {(\overrightarrow {{v_1}} + \overrightarrow {{v_2}} )^2} = {\overrightarrow {{v_1}} ^2} + {\overrightarrow {{v_2}} ^2} + 2\overrightarrow {{v_1}} .\overrightarrow {{v_2}} = |\overrightarrow {{v_1}} {|^2} + |\overrightarrow {{v_2}} {|^2} + 2|\overrightarrow {{v_1}} |.|\overrightarrow {{v_2}} |.\cos {45^o}$ $ = {750^2} + {40^2} + 2.750.40.\frac{{\sqrt 2 }}{2} \approx 606526,4068$.

Vậy $\left| {\overrightarrow v} \right| \approx 778,8$ (km/h).

Câu 3 :

Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:

Ngày	22	23	24	25	26	27	28	29	30	31
Nhiệt độ (độ C)	23	25	26	27	27	27	27	21	19	18

a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.

b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.

Phương pháp giải :

+ Viết mẫu số liệu theo thứ tự không tăng.

+ Dùng công thức tính số trung bình: $\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}$.

+ Tìm phương sai theo công thức ${S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + ... + {n_k}{x_k}^2} \right) - {\overline x ^2}$ và độ lệch chuẩn $S = \sqrt {{S^2}} $.

Lời giải chi tiết :

a) Viết mẫu số liệu theo thứ tự không tăng: 23; 25; 26; 27; 27; 27; 26; 21; 19; 18.

+ Số trung bình của mẫu số liệu là: $\overline x = \frac{{23 + 25 + 26 + 27 + 27 + 27 + 26 + 21 + 19 + 18}}{{10}} = 24$.

+ Phương sai: ${S^2} = \frac{1}{{10}}\left( {{{23}^2} + {{25}^2} + ... + {{18}^2}} \right) - {24^2} = 11,2$.

+ Độ lệch chuẩn: $S = \sqrt {{S^2}} = \sqrt {11,2} = \frac{{2\sqrt {70} }}{5}$.

👉

Giải bài nhanh với AI Hay:

Bài liên quan

Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 13

I. Phần trắc nghiệm
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 12

I. Phần trắc nghiệm
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 11

I. Phần trắc nghiệm
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 10

Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng? A. (forall x in mathbb{R},,x le {x^2}) B. (forall x in mathbb{R},,,left| x right| < 3 Leftrightarrow x < 3) C. (forall n in mathbb{N},,,{n^2} + 1)chia hết cho 3 D. (exists a in mathbb{Q},,{a^2} = 2)
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 9

Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Cố lên, sắp đói rồi! b) Số 15 là số nguyên tố. c) Tổng các góc của một tam giác là (180^circ .) d) (x) là số nguyên dương.