Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 6Tải về Câu 1: Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề? a) Huế là một thành phố của Việt Nam. b) Sông Hương chảy ngang qua thành phố Huế. c) Hãy trả lời câu hỏi này! d) 5 + 19 = 24. e) 6 + 81 = 25. f) Bạn có mang theo máy tính không? g) x + 2 = 11. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Phần 1: Trắc nghiệm (30 câu – 6 điểm) Câu 1: Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề? a) Huế là một thành phố của Việt Nam. b) Sông Hương chảy ngang qua thành phố Huế. c) Hãy trả lời câu hỏi này! d) \(5 + 19 = 24.\) e) \(6 + 81 = 25.\) f) Bạn có mang theo máy tính không? g) \(x + 2 = 11.\) A. 1. B. 2. C. 3. D. 4. Câu 2: Hãy viết số quy tròn của số gần đúng \(a = 17658\) biết \(\bar a = 17658\,\, \pm \,\,16.\) A. 17700. B. 17800. C. 17500. D. 17600. Câu 3: Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Đẳng thức nào sau đây sai? A. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \vec 0.\) B. \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\) C. \(\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {DA} + \overrightarrow {DC} } \right|.\) D. \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AB} + \overrightarrow {CB} .\) Câu 4: Lớp 10E có \(7\) học sinh giỏi Toán, \(5\) học sinh giỏi Lý, \(6\) học sinh giỏi Hóa, \(3\) học sinh giỏi cả Toán và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(2\) học sinh giỏi cả Lý và Hóa, \(1\) học sinh giỏi cả \(3\) môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10E là A. \(9.\) B. \(10.\) C. \(18.\) D. \(28.\) Câu 5: Miền nghiệm của bất phương trình: \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) - y + 3\) là nửa mặt phẳng chứa điểm: A. \(\left( {3;0} \right).\) B. \(\left( {3;1} \right).\) C. \(\left( {2;1} \right).\) D. \(\left( {0;0} \right).\) Câu 6: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
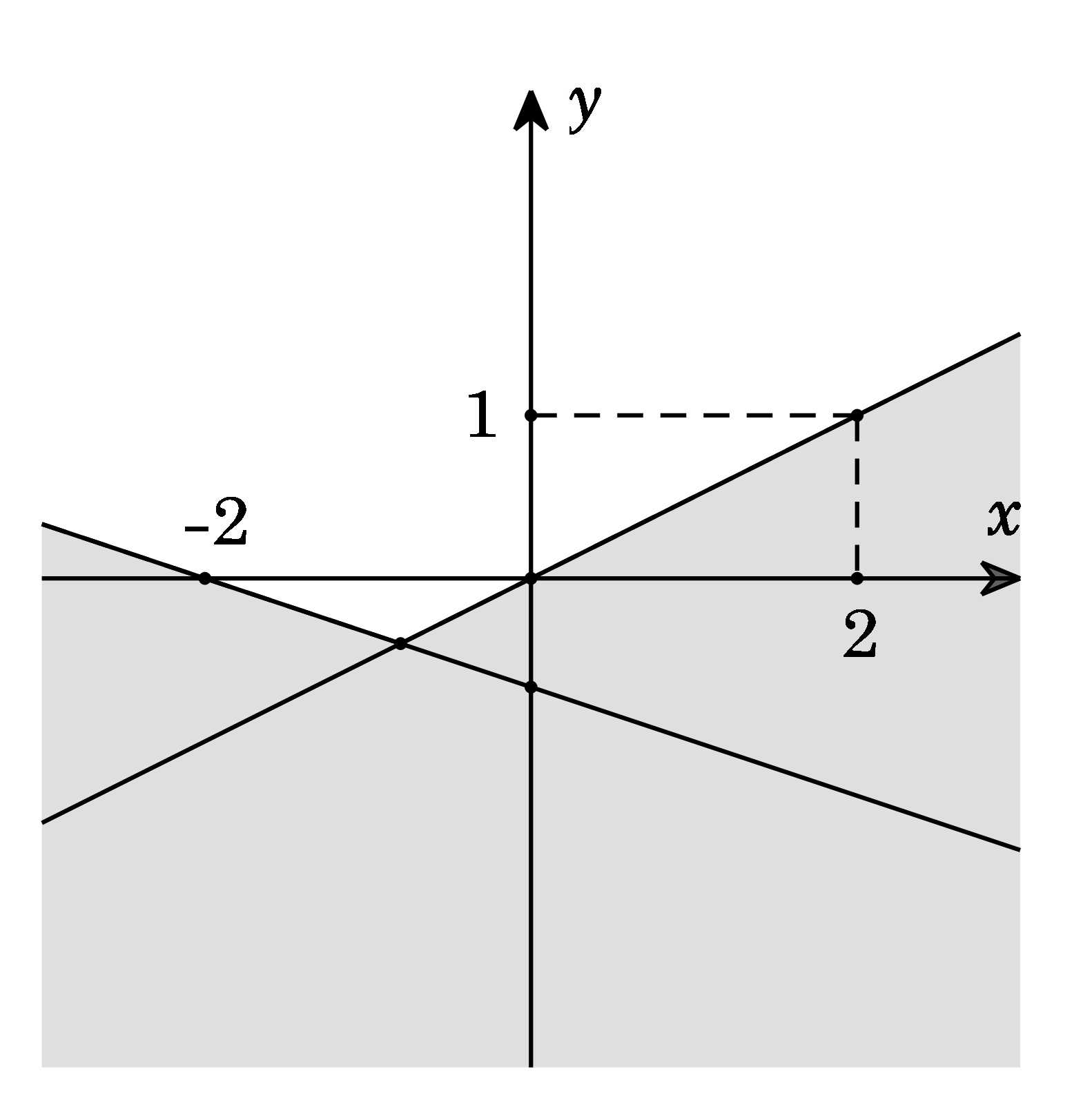
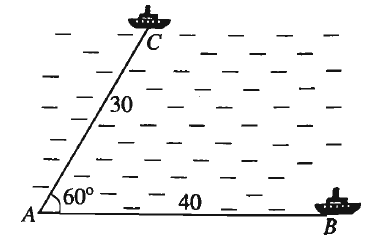
A. \(\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \ge - 2\end{array} \right..\) B. \(\left\{ \begin{array}{l}x - 2y > 0\\x + 3y < - 2\end{array} \right..\) C. \(\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \le - 2\end{array} \right..\) D. \(\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\end{array} \right..\) Câu 7: Tam giác \(ABC\) có \(AB = 3,{\rm{ }}AC = 6\) và \(\widehat A = 60^\circ \). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\). A. \(R = 3\). B. \(R = 3\sqrt 3 \). C. \(R = \sqrt 3 \). D. \(R = 6\). Câu 8: Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Kết quả gần nhất với số nào sau đây? A. \(61\) hải lí. B. \(36\) hải lí. C. \(21\) hải lí. D. \(18\) hải lí. Câu 9: Tính giá trị biểu thức \(S = {\sin ^2}15^\circ + {\cos ^2}20^\circ + {\sin ^2}75^\circ + {\cos ^2}110^\circ \). A. \(S = 0.\) B. \(S = 1.\) C. \(S = 2.\) D. \(S = 4.\) Câu 10: Cho hình vuông \(ABCD\) cạnh \(a\). Tính \(P = \overrightarrow {AC} .\left( {\overrightarrow {CD} + \overrightarrow {CA} } \right).\) A. \(P = - 1.\) B. \(P = 3{a^2}.\) C. \(P = - 3{a^2}.\) D. \(P = 2{a^2}.\) Câu 11: Có 100 học sinh dự thi học sinh giỏi Toán (điểm 20). Kết quả như sau:
Nhận xét nào sau đây là đúng? A. Phương sai lớn hơn 4, độ lệch chuẩn lớn hơn 2 B. Phương sai lớn hơn 5, độ lệch chuẩn lớn hơn 2 C. Phương sai nhỏ hơn 5, độ lệch chuẩn lớn hơn 2 D. Phương sai nhỏ hơn 4, độ lệch chuẩn nhỏ hơn 2 Câu 12: Cho tam giác ABC. Trên cạnh BC lấy điểm \(D\) sao cho \(\overrightarrow {BD} {\rm{\;}} = \frac{1}{3}\overrightarrow {BC} \). Khi đó, vectơ \(\overrightarrow {AD} \) bằng A. \(\frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) B. \(\frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) C. \(\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) D. \(\frac{5}{3}\overrightarrow {AB} {\rm{\;}} - \frac{1}{3}\overrightarrow {AC} \) Câu 13: Gọi \(G\) là trọng tâm của \(\Delta ABC\). Đặt \(\overrightarrow {GA} {\rm{\;}} = \vec a;\overrightarrow {GB} {\rm{\;}} = \vec b\). Xác định giá trị của \(m,{\mkern 1mu} {\mkern 1mu} n\) để \(\overrightarrow {BC} {\rm{\;}} = m\vec a + n\vec b\). A. \(m = 1,{\mkern 1mu} {\mkern 1mu} n = 2\) B. \(m = {\rm{\;}} - 1,{\mkern 1mu} {\mkern 1mu} n = {\rm{\;}} - 2\) C. \(m = 2,{\mkern 1mu} {\mkern 1mu} n = 1\) D. \(m = {\rm{\;}} - 2,{\mkern 1mu} {\mkern 1mu} n = {\rm{\;}} - 1\) Câu 14: Tam giác \(ABC\) có \(AC = 4,{\rm{ }}\widehat {BAC} = 30^\circ ,{\rm{ }}\widehat {ACB} = 75^\circ \). Tính diện tích tam giác \(ABC\). A. \({S_{\Delta ABC}} = 8\). B. \({S_{\Delta ABC}} = 4\sqrt 3 \). C. \({S_{\Delta ABC}} = 4\). D. \({S_{\Delta ABC}} = 8\sqrt 3 \). Câu 15: Độ lệch chuẩn đo mức độ phân tán của các số liệu trong mẫu quanh: A. Số mốt. B. Số trung vị. C. Số trung bình. D. Phương sai. Câu 16: Sản lượng lúa của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng tần số sau đây: (đơn vị: tạ)
Độ lệch chuẩn là A. 1,24 B. 1,54 C. 22,1 D. 4,70 Câu 17: Cho tập hợp \(A = {\rm{\{ }}x \in \mathbb{N}\left| x \right.\) là ước chung của \(36\;{\rm{v\`a }}\;{\rm{120\} }}\). Hãy liệt kê các phần tử của tập hợp \(A\). A. \(A = \left\{ {1;2;3;4;6;12} \right\}.\) B. \(A = \left\{ {1;2;4;6;8;12} \right\}.\) C. \(A = \left\{ {2;4;6;8;10;12} \right\}.\) D. \(A = \left\{ {1;36;120} \right\}.\) Câu 18: Cho hai tập hợp \(A = \left\{ {0;1;2;3;4} \right\},{\rm{ }}B = \left\{ {1;3;4;6;8} \right\}.\) Mệnh đề nào sau đây đúng? A. \(A \cap B = B.\) B. \(A \cup B = A.\) C. \(A\backslash B = \left\{ {0;2} \right\}.\) D. \(B\backslash A = \left\{ {0;4} \right\}.\) Câu 19: Điểm \(M\left( {0; - 3} \right)\) thuộc miền nghiệm của hệ bất phương trìnhnào sau đây? A. \(\left\{ \begin{array}{l}2x - y \le 3\\3x + 5y \le 1\end{array} \right..\) B. \(\left\{ \begin{array}{l}2x - y > 3\\3x + 5y \le - 3\end{array} \right..\) C. \(\left\{ \begin{array}{l}2x - y > - 3\\3x + 5y \ge 8\end{array} \right..\) D. \(\left\{ \begin{array}{l}2x - y \le - 3\\3x + 5y \ge 0\end{array} \right..\) Câu 20: Giá trị nhỏ nhất \({F_{\min }}\) của biểu thức \(F\left( {x;y} \right) = y--x\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là A. \({F_{\min }} = 1.\) B. \({F_{\min }} = 2.\) C. \({F_{\min }} = 3.\) D. \({F_{\min }} = 4.\) Câu 21: Tam giác \(ABC\) vuông ở \(A\) có góc \(\widehat B = {30^0}.\) Khẳng định nào sau đây là sai? A. \(\cos B = \frac{1}{{\sqrt 3 }}.\) B. \(\sin C = \frac{{\sqrt 3 }}{2}.\) C. \(\cos C = \frac{1}{2}.\) D. \(\sin B = \frac{1}{2}.\) Câu 22: Cho biết \(\tan \alpha = - 3.\) Giá trị của \(P = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }}\) bằng bao nhiêu? A. \(P = \frac{4}{3}.\) B. \(P = \frac{5}{3}.\) C. \(P = - \frac{4}{3}.\) D. \(P = - \frac{5}{3}.\) Câu 23: Cho tam giác ABC. Trên cạnh BC lấy điểm \(D\) sao cho \(\overrightarrow {BD} {\rm{\;}} = \frac{1}{3}\overrightarrow {BC} \). Khi đó, vectơ \(\overrightarrow {AD} \) bằng A. \(\frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) B. \(\frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) C. \(\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) D. \(\frac{5}{3}\overrightarrow {AB} {\rm{\;}} - \frac{1}{3}\overrightarrow {AC} \) Câu 24: Cho hai vecto \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) bất kỳ; \(\forall k,{\mkern 1mu} {\mkern 1mu} h \in \mathbb{R}\). Khẳng định nào sau đây không đúng? A. \(0.\vec a = 0\) B. \(k\left( {\vec a + \vec b} \right) = k\vec a + k\vec b\) C. \(k.\vec 0 = \vec 0\) D. \(h\left( {k\vec a} \right) = \left( {hk} \right)\vec a\) Câu 25: Tam giác \(ABC\) vuông tại \(A\) có \(AB = 6\)cm, \(BC = 10\)cm. Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho. A. \(r = 1\) cm. B. \(r = \sqrt 2 \) cm. C. \(r = 2\) cm. D. \(r = 3\) cm. Câu 26: Một miếng đất hình chữ nhật có chiều rộng \(x = 43{\rm{m}} \pm 0,5{\rm{m}}\) và chiều dài \(y = 63{\rm{m}} \pm 0,5{\rm{m}}\). Tính chu vi \(P\) của miếng đất đã cho. A. \(P = 212{\rm{m}} \pm 4{\rm{m}}.\) B. \(P = 212{\rm{m}} \pm 2{\rm{m}}.\) C. \(P = 212{\rm{m}} \pm 0,5{\rm{m}}.\) D. \(P = 212{\rm{m}} \pm 1{\rm{m}}.\) Câu 27: Khoảng biến thiên của mẫu số liệu 1 1 1 2 2 2 3 3 4 20 là: A. 1. B. 3,9. C. 19. D. 20. Câu 28: Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của \({\pi ^2}\) chính xác đến hàng phần nghìn. A. 9,873. B. 9,870. C. 9,872. D. 9,871. Câu 29: (ID: 592001) Cho ba điểm không thẳng hàng A, B, C. Điều kiện cần và đủ để ba điểm A, B, C thỏa mãn điều kiện \(\left( {\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} } \right).\overrightarrow {AB} {\rm{ \;}} = 0\) là: A. \(\Delta ABC\) đều. B. \(\Delta ABC\) cân tại C. C. \(\Delta ABC\) vuông tại C. D. \(\Delta ABC\) vuông cân tại C. Câu 30: Cho tam giác đều \(ABC\) có cạnh bằng \(a.\) Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {BC} .\) A. \(\overrightarrow {AB} .\overrightarrow {BC} = {a^2}.\) B. \(\overrightarrow {AB} .\overrightarrow {BC} = \frac{{{a^2}\sqrt 3 }}{2}.\) C. \(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}.\) D. \(\overrightarrow {AB} .\overrightarrow {BC} = \frac{{{a^2}}}{2}.\) Phần 2: Tự luận (4 điểm) Câu 1: Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:
(Nguồn: https://nchmf.gov.vn) a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên. b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó. Câu 2: Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn a) \(|\overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MC}}} | = |\overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MC}}} |\) b) \(|2\overrightarrow {{\rm{MA}}} + 3\overrightarrow {{\rm{MB}}} | = |3\overrightarrow {{\rm{MB}}} + 2\overrightarrow {{\rm{MC}}} |\) c) \(|4\overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MC}}} | = |2\overrightarrow {{\rm{MA}}} - \overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MC}}} |\) Câu 3: Đơn giản biểu thức \(B = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cot }^2}x - {{\tan }^2}x}} - {\cos ^2}x\).
----- HẾT ----- Lời giải HƯỚNG DẪN GIẢI CHI TIẾT Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1 (NB): Phương pháp: Mệnh đề là câu khẳng định có tính đúng hoặc sai. Cách giải: Các câu c), f), g) không phải là mệnh đề Chọn C. Câu 2 (TH): Cách giải: \(\bar a = 17658\,\, \pm \,\,16 \Rightarrow d = 16\) Hàng lớn nhất của d là hàng chục nên ta làm tròn số \(a = 17658\) đến hàng trăm, kết quả là: \(17700.\) Chọn A. Câu 3 (TH): Phương pháp: Sử dụng tính chất trung điểm: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \) với O là trung điểm của AB. Sử dụng quy tắc hình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) Cách giải:
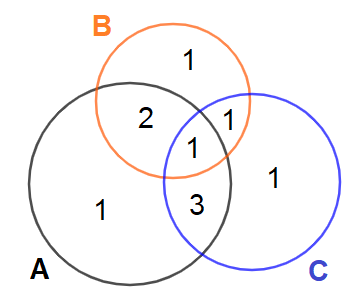
Xét các đáp án: Đáp án A. Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right) = \vec 0.\) Đáp án B. Ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành). Đáp án C. Ta có \(\left\{ \begin{array}{l}\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {BD} } \right| = BD\\\left| {\overrightarrow {DA} + \overrightarrow {DC} } \right| = \left| {\overrightarrow {DB} } \right| = BD\end{array} \right.\). Đáp án D. Do \(\overrightarrow {CD} \ne \overrightarrow {CB} \Rightarrow \left( {\overrightarrow {AB} + \overrightarrow {CD} } \right) \ne \left( {\overrightarrow {AB} + \overrightarrow {CB} } \right).\) Chọn D. Câu 4 (TH): Cách giải: Ta dùng biểu đồ Ven để giải: Gọi A là tập hợp các học sinh giỏi Toán của lớp 10E B là tập hợp các học sinh giỏi Lý của lớp 10E C là tập hợp các học sinh giỏi Hóa của lớp 10E \( \Rightarrow n(A) = 7;n(B) = 5;n(6)\) Hơn nữa \(n(A \cap B) = 3;n(A \cap C) = 4;n(B \cap C) = 2;n(A \cap B \cap C) = 1\) Số học sinh giỏi Toán và Lý mà không giỏi Hóa là: \(3 - 1 = 2\) (học sinh) Số học sinh giỏi Toán và Hóa mà không giỏi Lý là: \(4 - 1 = 3\) (học sinh) Số học sinh giỏi Lý và Hóa mà không giỏi Toán là: \(2 - 1 = 1\) (học sinh)
Số học sinh chỉ giỏi Toán là: \(7 - 2 - 1 - 3 = 1\) (học sinh) Số học sinh chỉ giỏi Lí là: \(5 - 2 - 1 - 1 = 1\) (học sinh) Số học sinh chỉ giỏi Hóa là: \(6 - 3 - 1 - 1 = 1\) (học sinh) Nhìn vào biểu đồ, số học sinh giỏi ít nhất \(1\) trong \(3\) môn là: \(1 + 2 + 1 + 3 + 1 + 1 + 1 = 10\) Chọn B. Câu 5 (TH): Cách giải: Ta có \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) - y + 3\, \Leftrightarrow \, - x + 3y - 1 > 0\). Vì \( - 2 + 3.1 - 1 > 0\) là mệnh đề đúng nên miền nghiệm của bất phương trình trên chứa điểm có tọa độ \(B\). Chọn C. Câu 6 (TH): Cách giải: Do miền nghiệm không chứa biên nên ta loại đáp án A và C. Chọn điểm \(M\left( {0;1} \right)\)thử vào các hệ bất phương trình. Xét đáp án B, ta có \(\left\{ \begin{array}{l}0 - 2.1 > 0\\0 + 3.1 < - 2\end{array} \right.\): Sai. Chọn D. Câu 7 (VD): Phương pháp: Áp dụng định lí cosin trong tam giác ABC tính BC: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A\). Cách giải: Áp dụng định lí Cosin, ta có \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A\) \( = {3^2} + {6^2} - 2.3.6.\cos {60^ \circ } = 27 \Leftrightarrow B{C^2} = 27 \Rightarrow B{C^2} + A{B^2} = A{C^2}.\) Suy ra tam giác ABC vuông tại B do đó bán kính \(R = \frac{{AC}}{2} = 3\) Chọn A. Câu 8 (TH): Cách giải: Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có và Áp dụng định lí côsin vào tam giác ABC ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A = {30^2} + {40^2} - 2.30.40.\cos {60^ \circ } = 900 + 1600 - 1200 = 1300\) Vậy \(BC = \sqrt {1300} \approx 36\)(hải lí). Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí. Chọn B. Câu 9 (TH): Phương pháp: Sử dụng \({\sin ^2}x + {\cos ^2}x = 1,{\mkern 1mu} {\mkern 1mu} \tan x = \frac{{\sin x}}{{\cos x}}\). Cách giải: Hai góc \({15^ \circ }\)và \({75^ \circ }\) phụ nhau nên \(\sin {75^ \circ } = \cos {15^ \circ }\) Hai góc \({20^ \circ }\) và \({110^ \circ }\) hơn kém nhau \({90^ \circ }\) nên \(\sin {20^ \circ } = - \cos {110^ \circ }\) Do đó, \(S = {\sin ^2}{15^ \circ } + {\cos ^2}{20^ \circ } + {\sin ^2}{75^ \circ } + {\cos ^2}{110^ \circ }\) \(\begin{array}{l} = {\sin ^2}{15^ \circ } + {\cos ^2}{20^ \circ } + {\cos ^2}{15^ \circ } + {\left( { - \sin {{20}^ \circ }} \right)^2}\\ = {\sin ^2}{15^ \circ } + {\cos ^2}{15^ \circ } + {\cos ^2}{20^ \circ } + {\sin ^2}{20^ \circ }\\ = 2\end{array}\) Chọn C. Câu 10 (VD): Phương pháp: Sử dụng quy tắc ba điểm, phép nhân vectơ với một số. Cách giải:
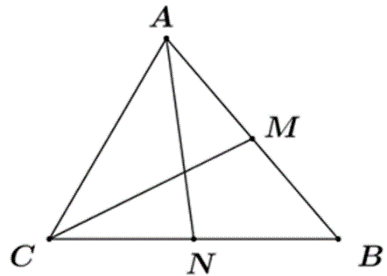
Từ giả thiết suy ra \(AC = a\sqrt 2 \) Ta có \(P = \overrightarrow {AC} .\left( {\overrightarrow {CD} + \overrightarrow {CA} } \right) = \overrightarrow {AC} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {CA} = - \overrightarrow {CA} .\overrightarrow {CD} - {\overrightarrow {AC} ^2}\) \( = - CA.CD.\cos \left( {\overrightarrow {CA} ,\overrightarrow {CD} } \right) - A{C^2} = - a\sqrt 2 .a.\cos {45^ \circ } - {\left( {a\sqrt 2 } \right)^2} = - 3{a^2}\) Chọn C. Câu 11 (VD): Phương pháp: Áp dụng công thức tìm phương sai và độ lệch chuẩn. Cách giải: Số trung bình cộng: \(\bar x = \frac{{9.1 + 10.1 + 11.3 + 12.5 + 13.8 + 14.13 + 15.19 + 16.24 + 17.14 + 18.10 + 19.2}}{{100}}\)\( = \frac{{1523}}{{100}} = 15,23\) (điểm) Phương sai: \({s^2} = \frac{1}{{100}}\left[ {1.{{\left( {9 - 15,23} \right)}^2} + 1.{{\left( {10 - 15,23} \right)}^2} + {\rm{\;}} \ldots {\rm{\;}} + 10.{{\left( {18 - 15,23} \right)}^2} + 2.{{\left( {19 - 15,23} \right)}^2}} \right]\) \( = 3,9571\)(điểm) Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)\( = \sqrt {3,9571} {\rm{\;}} \approx 1,989{\rm{2}}\) (điểm) Vậy phương sai nhỏ hơn \(4\), độ lệch chuẩn nhỏ hơn \(2\). Chọn D. Câu 12 (TH): Phương pháp: Áp dụng định nghĩa tích của vecto với một số, quy tắc cộng vecto để phân tích vecto. Cách giải:
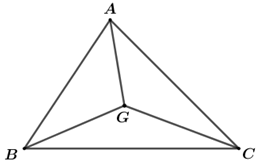
Ta có: \(\overrightarrow {AD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {BD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \) \({\mkern 1mu} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {AC} } \right)\)\( = \overrightarrow {AB} {\rm{\;}} - \frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)\({\mkern 1mu} {\mkern 1mu} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) \( \Rightarrow \overrightarrow {AD} {\rm{\;}} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) Chọn A. Câu 13 (TH): Phương pháp: Áp dụng phương pháp phân tích một vecto theo hai vecto cùng phương. Tính chất trọng tâm của tam giác. Cách giải:
Vì \(G\) là trọng tâm của \(\Delta ABC\) nên \(\overrightarrow {GA} {\rm{\;}} + \overrightarrow {GB} {\rm{\;}} + \overrightarrow {GC} {\rm{\;}} = \vec 0\)\( \Rightarrow \overrightarrow {GC} {\rm{\;}} = {\rm{\;}} - \overrightarrow {GA} {\rm{\;}} - \overrightarrow {GB} \) . Ta có: \(\overrightarrow {BC} {\rm{\;}} = \overrightarrow {BG} {\rm{\;}} + \overrightarrow {GC} \)\( \Rightarrow \overrightarrow {BC} {\rm{\;}} = {\rm{\;}} - \overrightarrow {GB} {\rm{\;}} + \overrightarrow {GC} \) \( \Rightarrow \overrightarrow {BC} {\rm{\;}} = {\rm{\;}} - \overrightarrow {GA} {\rm{\;}} - 2\overrightarrow {GB} {\rm{\;}} = {\rm{\;}} - \vec a - 2\vec b\)\( = {\rm{\;}} - \overrightarrow {GB} {\rm{\;}} - \overrightarrow {GA} {\rm{\;}} - \overrightarrow {GB} \) \( = {\rm{\;}} - \overrightarrow {GA} {\rm{\;}} - 2\overrightarrow {GB} \) Mà \(\overrightarrow {BC} {\rm{\;}} = m\vec a + n\vec b\) suy ra \(m = {\rm{\;}} - 1,{\mkern 1mu} {\mkern 1mu} n = {\rm{\;}} - 2\). Chọn B. Câu 14 (TH): Cách giải: Ta có \(\widehat {ABC} = {180^ \circ } - \left( {\widehat {BAC} + \widehat {ACB}} \right) = {75^ \circ } = \widehat {ACB}\) Suy ra tam giác ABC cân tại A nên AB=AC=4. Diện tích tam giác ABC là \({S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin \widehat {BAC} = 4\) Chọn C. Câu 15 (NB): Phương pháp: Áp dụng lý thuyết về độ lệch chuẩn. Cách giải: Độ lệch chuẩn là căn bậc hai của phương sai. Do đó, độ lệch chuẩn cũng là một số đo mức độ phân tán các giá trị trong mẫu số liệu quanh số trung bình. Chọn C. Câu 16 (TH): Phương pháp: Đối với bảng phân bố tần số, phương sai được tính theo công thức: \({s^2} = \frac{1}{N}\left[ {{n_1}{{\left( {{x_1} - \bar x} \right)}^2} + {n_2}{{\left( {{x_2} - \bar x} \right)}^2} + {\rm{\;}} \ldots {\rm{\;}} + {n_k}{{\left( {{x_k} - \bar x} \right)}^2}} \right]\) Với \({n_i};{\mkern 1mu} {\mkern 1mu} {f_i}\) lần lượt là tần số, tần suất của giá trị \({x_i}\). Cách giải: Bảng phân số tần số:
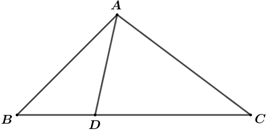
*) Sản lượng trung bình của 40 thửa ruộng là: \(\bar x = \frac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}} = 22,1{\mkern 1mu} \)(tạ) *) Phương sai: \({s^2} = \frac{1}{{40}}\left[ {5.{{\left( {20 - 22,1} \right)}^2} + 8.{{\left( {21 - 22,1} \right)}^2} + 11.{{\left( {22 - 22,1} \right)}^2} + 10.{{\left( {23 - 22,1} \right)}^2} + 6.{{\left( {24 - 22,1} \right)}^2}} \right]\)\( = 1,54\) (tạ) *) Độ lệch chuẩn \(s = \sqrt {1,54} \approx 1,24\) Chọn A. Câu 17 (NB): Phương pháp: Liệt kê các ước chung của 36 và 120. Cách giải: Ta có \(\left\{ \begin{array}{l}36 = {2^2}{.3^2}\\120 = {2^3}.3.5\end{array} \right.\). Do đó \(A = \left\{ {1;2;3;4;6;12} \right\}\). Chọn A. Câu 18 (NB): Phương pháp: \(A \cap B = \{ x \in A\) và \(x \in B\} .\) \(A \cup B = \{ x \in A\) hoặc \(x \in B\} .\) \(A\backslash B = \{ x \in A\) và \(x \notin B\} .\) Cách giải: Ta có: \(A = \left\{ {0;1;2;3;4} \right\},{\rm{ }}B = \left\{ {1;3;4;6;8} \right\}.\) \(A \cap B = \{ 1;3;4\} \ne B.\) \(A \cup B = \{ 0;1;2;3;4;6;8\} \ne A.\) \(A\backslash B = \left\{ {0;2} \right\}.\) \(B\backslash A = \{ 6;8\} \ne \left\{ {0;4} \right\}.\) Chọn C. Câu 19 (NB): Phương pháp: Thay tọa độ điểm M vào từng hệ bất phương trình. Cách giải: Thay tọa độ \(M\left( {0; - 3} \right)\) vào biểu thức \(2x - y\)ta được: \(2.0 - ( - 3) = 3\) \( \Rightarrow \)Loại B, D. Thay tọa độ \(M\left( {0; - 3} \right)\) vào biểu thức \(3x + 5y\)ta được: \(3.0 + 5.( - 3) = - 15\) \( \Rightarrow \)Loại C Chọn A. Câu 20 (TH): Phương pháp: Bước 1. Biểu diễn miền nghiệm của hệ BPT Bước 2. Xác định tọa độ đỉnh của miền nghiệm Bước 3. Tính giá trị của F tại các đỉnh. KL giá trị nhỏ nhất. Cách giải: Ta có \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y - 2x - 2 \le 0}\\{2y - x - 4 \ge 0}\\{x + y - 5 \le 0}\end{array}} \right..\) \(\left( * \right)\) Trong mặt phẳng tọa độ \(Oxy,\)vẽ các đường thẳng \(\begin{array}{l}{d_1}:y - 2x - 2 = 0,\,\,{\rm{ }}{d_2}:2y - x - 4 = 0,{\rm{ }}\\{\rm{ }}{d_3}:x + y - 5 = 0.\end{array}\) Khi đó miền nghiệm của hệ bất phương trình \(\left( * \right)\) là phần mặt phẳng (tam giác \(ABC\) kể cả biên) tô màu như hình vẽ. Xét các đỉnh của miền khép kín tạo bởi hệ \(\left( * \right)\) là \(A\left( {0;2} \right),{\rm{ }}B\left( {2;3} \right),{\rm{ }}C\left( {1;4} \right).\) Ta có \(\left\{ \begin{array}{l}F\left( {0;2} \right) = 2\\F\left( {2;3} \right) = 1\\F\left( {1;4} \right) = 3\end{array} \right. \Rightarrow {\rm{ }}{F_{\min }} = 1{\rm{ }}{\rm{.}}\) Chọn A. Câu 21 (TH): Phương pháp: Sử dụng bảng giá trị lượng giác của các góc đặc biệt. Cách giải: Từ giả thiết suy ra \(\widehat C = {60^ \circ }\) Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được \(\cos B = \cos {30^ \circ } = \frac{{\sqrt 3 }}{2}\) Chọn A. Câu 22 (VD): Phương pháp: Chia cả tử và mẫu biểu thức P cho \(\cos \alpha \) và biểu diễn biểu thức P theo \(\tan \alpha \). Cách giải: Ta có \(P = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }} = \frac{{6\frac{{\sin \alpha }}{{\cos \alpha }} - 7}}{{6 + 7\frac{{\sin \alpha }}{{\cos \alpha }}}} = \frac{{6\tan \alpha - 7}}{{6 + 7\tan \alpha }} = \frac{5}{3}\) Chọn B. Câu 23 (TH): Phương pháp: Áp dụng định nghĩa tích của vecto với một số, quy tắc cộng vecto để phân tích vecto. Cách giải:
Ta có: \(\overrightarrow {AD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {BD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \) \({\mkern 1mu} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {AC} } \right)\)\( = \overrightarrow {AB} {\rm{\;}} - \frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)\({\mkern 1mu} {\mkern 1mu} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) \( \Rightarrow \overrightarrow {AD} {\rm{\;}} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) Chọn A. Câu 24 (NB): Phương pháp: Áp dụng các tính chất của phép nhân véctơ với một số. Cách giải: Với \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) tùy ý; \(\forall k,{\mkern 1mu} {\mkern 1mu} h \in \mathbb{R}\) ta có: +) \(0.\vec a = 0\) là đáp án sai vì \(0.\vec a = \vec 0\). +) \(k\left( {\vec a + \vec b} \right) = k\vec a + k\vec b\) (đúng) +) \(k.\vec 0 = \vec 0\) (đúng) +) \(h\left( {k\vec a} \right) = \left( {hk} \right)\vec a\) (đúng) Chọn A. Câu 25 (NB): Cách giải: Dùng Pitago tính được \(AC = 8\), suy ra \(p = \frac{{AB + BC + CA}}{2} = 12\) Diện tích tam giác vuông \(S = \frac{1}{2}AB.AC = 24\) .Lại có \(S = p.r \Rightarrow r = \frac{S}{p}2cm\) Chọn C. Câu 26 (TH): Cách giải: Chu vi của miếng đất là \(P = 2\left[ {x + y} \right] = 2.\left[ {\left( {43 \pm 0,5} \right) + \left( {63 \pm 0,5} \right)} \right]\) \( = 2.\left[ {\left( {43 + 63} \right) \pm \left( {0,5 + 0,5} \right)} \right] = 212 \pm 2.\) Chọn B. Câu 27 (TH): Phương pháp: Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất. Cách giải: Giá trị lớn nhất là 20 Giá trị nhỏ nhất là 1 Vậy khoảng biến thiên của mẫu số liệu là: \(R = 20 - 1 = 19\) Chọn C. Câu 28 (TH): Cách giải: Sử dụng máy tính cầm tay ta được \({\pi ^2} = 9,8696044011...\) Làm tròn đến hàng phần nghìn ta được kết quả:\(9,870.\) Chọn B. Câu 29 (TH): Phương pháp: Sử dụng quy tắc hình bình hành. Sử dụng: hai vectơ vuông góc với nhau thì tích vô hướng bằng 0. Cách giải:
Lấy D sao cho ACBD là hình bình hành, khi đó ta có: \(\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} {\rm{ \;}} = \overrightarrow {CD} \). Theo bài ra ta có: \(\left( {\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} } \right).\overrightarrow {AB} {\rm{ \;}} = 0 \Leftrightarrow \overrightarrow {CD} .\overrightarrow {AB} {\rm{ \;}} = 0\) \( \Rightarrow CD \bot AB\). Hình bình hành ACBD có hai đường chéo vuông góc nên là hình thoi, do đó CA = CB. Vậy tam giác ABC cân tại C. Chọn B. Câu 30 (NB): Phương pháp: Sử dụng định nghĩa tích vô hướng của hai vectơ:\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) Cách giải: Xác định được góc \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\) là góc ngoài của góc \(\widehat B\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {120^ \circ }\) Do đó \(\overrightarrow {AB} .\overrightarrow {BC} = AB.BC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = a.a.\cos {120^ \circ } = - \frac{{{a^2}}}{2}\) Chọn C.
Phần 2: Tự luận (4 điểm) Câu 1 (VD): Phương pháp: a) * Số trung bình của mẫu số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2},{\mkern 1mu} {\mkern 1mu} ....,{\mkern 1mu} {\mkern 1mu} {x_n}\) kí hiệu là \(\bar x\), được tính bằng công thức: \(\bar x = \frac{{{m_1}{x_2} + {m_2}{x_2} + ... + {m_k}{x_k}}}{n}\) Trong đó mk là tần số của giá trị xk và \(n = {m_1} + {m_2} + ... + {m_k}\). Cách giải: a) Mẫu số liệu thống kê nhiệt độ nhận được từ bảng là: 23 25 26 27 27 27 27 21 19 18 b) * Nhiệt độ trung bình của 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 là: \(\bar x = \frac{{23 + 25 + 26 + 27 + 27 + 27 + 27 + 21 + 19 + 18}}{{10}} = 24\) (\(^oC\)) * Phương sai \({s^2} = \frac{1}{{10}}({23^2} + {25^2} + {26^2} + {4.27^2} + {21^2} + {19^2} + {18^2}) - {24^2} = 11,2\) * Độ lệch chuẩn \(s = \sqrt {11,2} \approx 3,35\) Câu 2 (VD): Cách giải:
a) Gọi I là trung điểm \({\rm{BC}}\) ta có: \(|\overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MC}}} | = |\overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MC}}} | \Leftrightarrow {\rm{ }}|\overrightarrow {{\rm{MI}}} | = |\overrightarrow {{\rm{CB}}} | \Leftrightarrow {\rm{MI}} = \frac{{{\rm{BC}}}}{2}\) Vậy tập hợp điểm \({\rm{M}}\) là đường tròn tâm \({\rm{I}}\), bán kính \({\rm{R}} = \frac{{{\rm{BC}}}}{2}\). b) Gọi \({\rm{K}}\) là điểm thoả mān: L là điểm thoả mān: \(3\overrightarrow {{\rm{LB}}} + 2\overrightarrow {{\rm{LC}}} = \vec 0\) Ta có: \(|2\overrightarrow {{\rm{MA}}} + 3\overrightarrow {{\rm{MB}}} | = |3\overrightarrow {{\rm{MB}}} + 2\overrightarrow {{\rm{MC}}} |\) \( \Leftrightarrow |5\overrightarrow {{\rm{MK}}} | = |5\overrightarrow {{\rm{ML}}} | \Leftrightarrow {\rm{MK}} = {\rm{ML}}\) \( \Rightarrow \) Tập hợp điểm \({\rm{M}}\) là đường trung trực của đoạn thẳng \({\rm{KL}}\). c) Với I là trung điểm của \({\rm{BC}}\). Gọi \({\rm{J}}\) là điểm thoả mān: \(4\overrightarrow {{\rm{JA}}} + \overrightarrow {{\rm{JB}}} + \overrightarrow {{\rm{JC}}} = \vec 0\) Ta có: \(|4\overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MC}}} | = |2\overrightarrow {{\rm{MA}}} - \overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MC}}} |\) \( \Leftrightarrow |6\overrightarrow {{\rm{MJ}}} | = |2\overrightarrow {{\rm{MA}}} - 2\overrightarrow {{\rm{MI}}} | \Leftrightarrow |6\overrightarrow {{\rm{MJ}}} | = |2\overrightarrow {{\rm{IA}}} | \Leftrightarrow {\rm{MJ}} = \frac{1}{3}{\rm{IA}} = \) const Vậy tập hợp điểm \(M\) là đường tròn tâm \({\rm{J}}\) bán kính \({\rm{R}} = \frac{1}{3}{\rm{IA}}\). Câu 3 (VD): Phương pháp: Sử dụng \(\tan x = \frac{{\sin x}}{{\cos x}},{\mkern 1mu} {\mkern 1mu} \cot x = \frac{{\cos x}}{{\sin x}}\), quy đồng, sử dụng hằng đẳng thức để rút gọn. Cách giải: \(\begin{array}{*{20}{l}}{B = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cot }^2}x - {{\tan }^2}x}} - {{\cos }^2}x}\\{B = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{\frac{{{{\cos }^2}x}}{{{{\sin }^2}x}} - \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}}} - {{\cos }^2}x}\\{B = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{\frac{{{{\cos }^4}x - {{\sin }^4}x}}{{{{\sin }^2}x{{\cos }^2}x}}}} - {{\cos }^2}x}\\{B = \frac{{\left( {{{\cos }^2}x - {{\sin }^2}x} \right){{\sin }^2}x{{\cos }^2}x}}{{\left( {{{\cos }^2}x - {{\sin }^2}x} \right)\left( {{{\cos }^2}x + {{\sin }^2}x} \right)}} - {{\cos }^2}x}\\{B = {{\sin }^2}x{{\cos }^2}x - {{\cos }^2}x}\\{B = {{\cos }^2}x\left( {{{\sin }^2}x - 1} \right)}\\{B = - {{\cos }^4}x}\end{array}\)
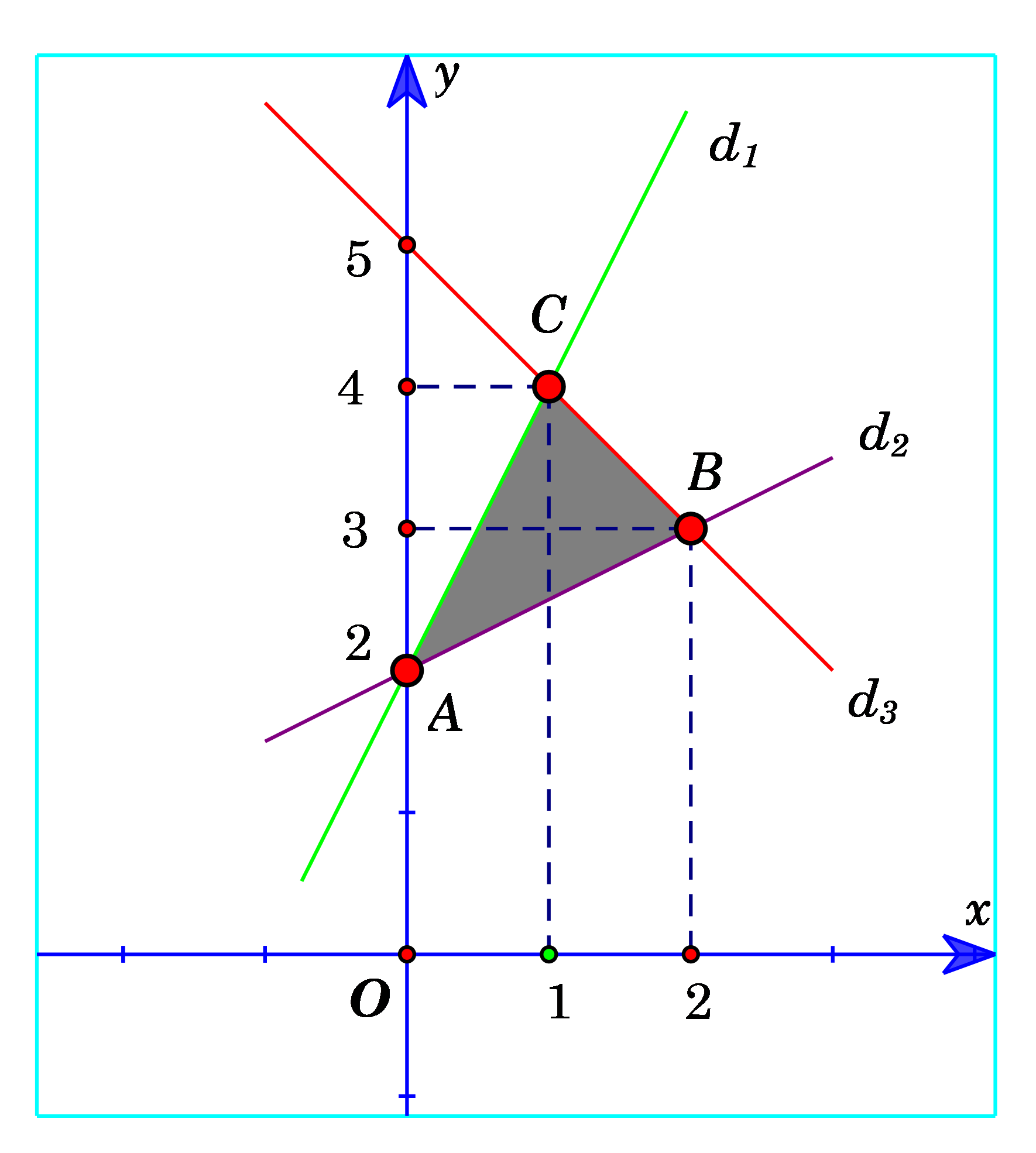
|
























Danh sách bình luận