Đề thi giữa kì 2 Toán 10 Kết nối tri thức - Đề số 2

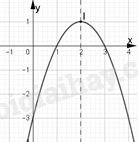
Đề bài

Phần trắc nghiệm (7 điểm)

Câu 1: Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}x + \sqrt {x - 2} ,\,\,khi\,\,x \ge 2\\1 - 3x,\,\,\,khi\,\,x < 2\end{array} \right.$. Giá trị $f\left( 1 \right)$ bằng

A. $- 2$.

B. $0$.

C. không xác định.

D. $2$.

Câu 2: Tập xác định của hàm số $y = \frac{1}{x} + \sqrt {3 - x}$ là

A. $\left( { - \infty ;3} \right]$.

B. $\left[ {3; + \infty } \right)$.

C. $\mathbb{R}\backslash \left\{ 0 \right\}$.

D. $\left( { - \infty ;3} \right]\backslash \left\{ 0 \right\}$.

Câu 3: Cho hàm số $y = f\left( x \right) = {x^2}$ xác định trên $\mathbb{R}.$ Xét các mệnh đề sau:

Hàm số $y = f\left( x \right)$ đồng biến trên $\mathbb{R}.$

Hàm số $y = f\left( x \right)$ nghịch biến trên $\left( {0; + \infty } \right).$

Hàm số $y = f\left( x \right)$ đồng biến trên $\left( { - \infty ;0} \right).$

Tìm tất cả các mệnh đề sai trong ba mệnh đề trên.

A. I và II.

B. I và III.

C. II và III.

D. I, II và III.

Câu 4: Cho hàm số $y = 2{x^2} + 4x - 2023$. Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên khoảng $\left( { - \infty ; - 2} \right)$ và nghịch biến trên khoảng $\left( { - 2; + \infty } \right)$.

B. Hàm số nghịch biến trên khoảng $\left( { - \infty ; - 2} \right)$ và đồng biến trên khoảng $\left( { - 2; + \infty } \right)$.

C. Hàm số đồng biến trên khoảng $\left( { - \infty ; - 1} \right)$ và nghịch biến trên khoảng $\left( { - 1; + \infty } \right)$.

D. Hàm số nghịch biến trên khoảng $\left( { - \infty ; - 1} \right)$ và đồng biến trên khoảng $\left( { - 1; + \infty } \right)$.

Câu 5: Hàm số nào có đồ thị như hình vẽ bên dưới?

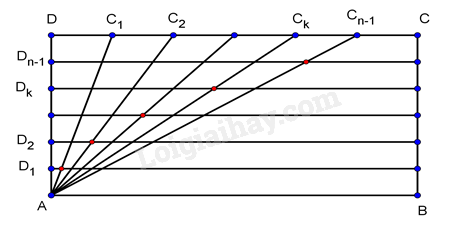
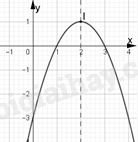
A. $y =  - {x^2} + 4x - 3$.

B. $y =  - {x^2} - 4x - 3$.

C. $y =  - 2{x^2} - x - 3$.

D. $y = {x^2} - 4x - 3$.

Câu 6: Tọa độ giao điểm của $\left( P \right)\,:\,y = {x^2} - 4x$ với đường thẳng $d\,:\,y =  - x - 2$ là

A. $M\left( {0;\, - 2} \right)$, $N\left( {2;\, - 4} \right)$.

B. $M\left( { - 1;\, - 1} \right)$, $N\left( { - 2;\,0} \right)$.

C. $M\left( {\, - 3;\,1} \right)$, $N\left( {3;\, - 5} \right)$.

D. $M\left( {1;\, - 3} \right)$, $N\left( {2;\, - 4} \right)$.

Câu 7: Trong các biểu thức sau, biểu thức nào là tam thức bậc 2?

A. $f(x) = x + 3$.

B. $f(x) = (m - 1){x^2} + 2x + 5$.

C. $f(x) = 2{x^2} + x - 5$.

D. $f(x) = \frac{{{x^2} + 1}}{{x - 2}}$.

Câu 8: Cho tam thức bậc hai $f\left( x \right) = a{x^2} + bx + c\;\;\left( {a \ne 0} \right)$. Khẳng định nào sau đây đúng?

A. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta  < 0\end{array} \right.$.

B. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  > 0\end{array} \right.$.

C. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta  > 0\end{array} \right.$.

D. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  < 0\end{array} \right.$.

Câu 9: Bảng xét dấu sau đây là của tam thức bậc 2 nào?

A. $f(x) =  - {x^2} + 5x - 6$.

B. $f(x) = {x^2} + 5x - 6$.

C. $f(x) = {x^2} - 5x - 6$.

D. $f(x) =  - {x^2} - 5x + 6$.

Câu 10: Tập nghiệm của phương trình $\sqrt {{x^2} + 3x - 2}  = \sqrt {1 + x}$ là

A. $\emptyset$

B. $\left\{ { - 3} \right\}$

C. $\left\{ {1; - 3} \right\}$.

D. $\left\{ 1 \right\}$.

Câu 11: Phương trình $\sqrt {3{x^2} + 6x + 3}  = 2x + 1$có tập nghiệm là :

A. $\left\{ {1 - \sqrt 3 ;1 + \sqrt 3 } \right\}$.

B. $\left\{ {1 - \sqrt 3 } \right\}$.

C. $\left\{ {1 + \sqrt 3 } \right\}$

D. $\emptyset$.

Câu 12: Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $d$ có phương trình $\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - t\end{array} \right.,t \in \mathbb{R}$. Xác định một vectơ pháp tuyến của đường thẳng $d$

A. $\overrightarrow n  = \left( {1;2} \right)$.

B. $\overrightarrow n  = \left( {2; - 1} \right)$.

C. $\overrightarrow n  = \left( { - 2;1} \right)$.

D. $\overrightarrow n  = \left( { - 1;2} \right)$.

Câu 13: Trong mặt phẳng tọa độ $Oxy$, viết phương trình đường thẳng đi qua điểm $M\left( {2; - 3} \right)$ và có một vectơ pháp tuyến $\overrightarrow n  = \left( {2;1} \right)$

A. $x + y + 1 = 0$.

B. $2x + y - 5 = 0$.

C. $2x - 3y - 1 = 0$.

D. $2x + y - 1 = 0$.

Câu 14: Trong mặt phẳng tọa độ $O\,xy$, cho hai đường thẳng ${d_1}:2x - y\, + \,3 = 0$ và ${d_2}:x + 2y\, + \,1 = 0$. Vị trí tương đối của hai đường thẳng ${d_1}$ và ${d_2}$ là

A. ${d_1}\, \equiv \,{d_2}$.

B. ${d_1}\,{\rm{//}}\,{d_2}$.

C. ${d_1} \bot \,\,{d_2}$.

D. Cắt nhau và không vuông góc.

Câu 15: Trong mặt phẳng $Oxy,$ góc giữa hai đường thẳng ${\Delta _1}:\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 - 2t\end{array} \right.$ và ${\Delta _2}:\left\{ \begin{array}{l}x =  - 3 + 2t\\y = 1 + 3t\end{array} \right.$ bằng

A. $90^\circ$.

B. $45^\circ$.

C. $60^\circ$.

D. $30^\circ$.

Câu 16: Trong mặt phẳng $Oxy$, cho điểm $M\left( { - 2\,\,;\,\,1} \right)$ và đường thẳng $\Delta :\,\,x - 3y + 6 = 0$. Khoảng cách từ điểm $M$ đến đường thẳng $\Delta$ bằng

A. $\frac{{\sqrt {10} }}{{10}}.$

B. $2\sqrt {10} .$

C. $\frac{{\sqrt {10} }}{5}.$

D. $\frac{2}{{\sqrt {10} }}.$

Câu 17: Phương trình nào sau đây không phải là phương trình đường tròn?

A. ${x^2} + {y^2} - 100y + 1 = 0$.

B. ${x^2} + {y^2} - y = 0$.

C. ${x^2} + {y^2} - 2 = 0$.

D. ${x^2} + {y^2} - x + y + 4 = 0$.

Câu 18: Viết phương trình đường tròn có tâm $A\left( {2\;;\; - 5} \right)$ và tiếp xúc với đường thẳng

$d:3x - 4y - 1 = 0$.

A. ${\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 25$.

B. ${\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 25$.

C. ${\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 5$.

D. ${\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 5$.

Câu 19: Tọa độ các đỉnh của hypebol $\left( H \right):\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} = 1$ là

A. ${A_1} = \left( { - 5;0} \right);{A_2} = \left( {5;0} \right)$.

B. ${A_1} = \left( {0; - 4} \right);{A_2} = \left( {0;4} \right)$.

C. ${A_1} = \left( { - 4;0} \right);{A_2} = \left( {4;0} \right)$.

D. ${A_1} = \left( {0; - 5} \right);{A_2} = \left( {0;5} \right)$.

Câu 20: Cho Parapol$\left( P \right):{y^2} = 2px\,\left( {p > 0} \right)$. Chọn mệnh đề đúng trong các mệnh đề sau:

A. $\left( P \right)$ có tiêu điểm $F\left( {0\,;\,\frac{p}{2}} \right).$

B. $\left( P \right)$ có tiêu điểm $F\left( { - \frac{p}{2}\,;\,0} \right).$

C. $\left( P \right)$ có phương trình đường chuẩn $\Delta :y = \frac{p}{2}.$

D. $\left( P \right)$ có phương trình đường chuẩn $\Delta :x =  - \frac{p}{2}.$

Câu 21: Tìm tập xác định ${\rm{D}}$ của hàm số $y = \frac{{x + 1}}{{\left( {x - 3} \right)\sqrt {2x - 1} }}$.

A. ${\rm{D}} = \left( { - \frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}$.

B. ${\rm{D}} = \left[ {\frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}$.

C. ${\rm{D}} = \left( {\frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}$.

D. ${\rm{D}} = \mathbb{R}$.

Câu 22: Có bao nhiêu số nguyên $m \in \left[ { - 2022;\,2022} \right]$để hàm số $y = \sqrt {m - 2x}$ xác định trên khoảng $\left( { - 3; - 1} \right)$?

A. $2022$.

B. $2025$.

C. $2021$.

D. $4042$.

Câu 23: Tìm tất cả các giá trị của tham số $m$để hàm số $y = f\left( x \right) = \left( {m - 4} \right)x + {m^2} - m - 2$ đồng biến trên tập xác định của nó.

A. $m > 4$.

B. $m \ge 4$.

C. $m < 4$.

D. $m \le 4$.

Câu 24: Biết rằng $\left( P \right):y = a{x^2} - 4x + c$ có hoành độ đỉnh bằng $- 3$ và đi qua điểm $M\left( { - 2;1} \right)$. Tính tổng $S = a + c$

A. $S = 5$.

B. $S =  - 5$.

C. $S = 4$.

D. $S = 1$.

Câu 25: Xác định $\left( P \right):y = a{x^2} - 6x + c$, biết $\left( P \right)$ có trục đối xứng $x =  - 4$ và cắt $Ox$ tại hai điểm có độ dài bằng $4$.

A. $\left( P \right):y =  - \frac{3}{4}{x^2} - 6x - 9$.

B. $\left( P \right):y = \frac{3}{4}{x^2} - 6x - 9$.

C. $\left( P \right):y =  - \frac{3}{4}{x^2} - 6x + 9$.

D. $\left( P \right):y = \frac{3}{4}{x^2} - 6x + 9$.

Câu 26: Tìm tập xác định của hàm số $y = \sqrt {2{x^2} - 5x + 2}$.

A. $\left( { - \infty ;\frac{1}{2}} \right]$.

B. $\left[ {2; + \infty } \right)$.

C. $\left( { - \infty ;\frac{1}{2}} \right] \cup \left[ {2; + \infty } \right)$.

D. $\left[ {\frac{1}{2};2} \right]$.

Câu 27: Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $\left( {2{m^2} + m - 6} \right){x^2} + \left( {2m - 3} \right)x - 1 > 0$?

A. $- \frac{5}{6} < m \le \frac{3}{2}$.

B. $- \frac{5}{6} < m < \frac{3}{2}$.

C. $- \frac{5}{6} \le m < \frac{3}{2}$.

D. $- \frac{5}{6} \le m \le \frac{3}{2}$.

Câu 28: Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \sqrt {\left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1}$ có tập xác định là $\mathbb{R}$?

A. $m > \frac{7}{3}$.

B. $m < \frac{7}{3}$.

C. $m \le \frac{7}{3}$.

D. $m \ge \frac{7}{3}$.

Câu 29: Phương trình $\sqrt {{x^2} + 2x - 3}  = 5 - x$ có nghiệm là $x = \frac{a}{b}$. Khi đó $a + 2b$bằng:

A. $10$.

B. $33$.

C. $17$.

D. $13$.

Câu 30: Phương trình tổng quát của đường thẳng $d$ đi qua $A\left( {1; - 2} \right)$ và vuông góc với đường thẳng $\Delta :3x - 2y + 1 = 0$ là:

A. $3x - 2y - 7 = 0.$

B. $2x + 3y + 4 = 0.$

C. $x + 3y + 5 = 0.$

D. $2x + 3y - 3 = 0.$

Câu 31: Trong mặt phẳng $Oxy,$ gọi S là tập hợp tất cả các giá trị của tham số m để góc giữa hai đường thẳng $d:mx + \left( {m - 1} \right)y + 2 = 0$ và $\Delta :x - y + 2 = 0$ bằng $30^\circ .$ Tích tất cả các phần tử của tập S bằng

A. $1$.

B. $- \frac{1}{6}$.

C. $\frac{1}{6}$.

D. $- 1$.

Câu 32: Tâm đường tròn ${x^2} + {y^2} - 10x + 1 = 0$ cách trục $Oy$ một khoảng bằng

A. $5$.

B. $0$.

C. $10$.

D. $- 5$.

Câu 33: Tìm tất cả giá trị của tham số $m$ để phương trình ${x^2} + {y^2} + 2mx - 10y + 4m = 0$ là

phương trình đường tròn và có bán kính nhỏ nhất.

A. $m = \frac{1}{2}$.

B. $m = 1$.

C. $m =  - 2$.

D. $m = 2$.

Câu 34: Tổng các khoảng cách từ một điểm bất kỳ nằm trên elip $\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$ tới hai tiêu điểm bằng

A. $4.$

B. $6.$

C. $12.$

D. $\sqrt 5 .$

Câu 35: Cho của hypebol $\left( H \right):\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{5} = 1$. Hiệu các khoảng cách từ mỗi điểm nằm trên $\left( H \right)$ đến hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?

A. $8$.

B. $16$.

C. $4$.

D. $5$.

Phần tự luận (3 điểm)

Bài 1. Một công ty bắt đầu sản xuất và bán một loại xe máy từ năm 2018. Số lượng loại xe máy đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 4 nghìn và $4,5$ nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm kể từ 2018, số lượng xe máy loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm số bậc hai. Giả sử $t$ là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại xe máy đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diễn bởi các điểm $\left( {0;\,4} \right)$ và $\left( {1;\,4,5} \right)$. Giả sử điểm $\left( {0;\,4} \right)$ là đỉnh đồ thị của hàm số bậc hai này. Hỏi đến năm bao nhiêu thì số lượng xe máy đó bán được trong năm sẽ vượt mức 40 nghìn chiếc?

Bài 2. Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $d$ đi qua điểm $M\left( {1;2} \right)$ và cắt tia $Ox$, tia $Oy$ lần lượt tại $A,B$ sao cho tam giác $OAB$ có diện tích nhỏ nhất. Hãy viết phương trình của $d.$

Bài 3. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ $Oth,$ trong đó $t$ là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; $h$ là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao $1,2m$. Sau đó $1$ giây, nó đạt độ cao $8,5m$và $2$ giây sau khi đá lên, nó đạt độ cao $6m$. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm)?

Bài 4. Cho hình chữ nhật $ABCD$ ( tham khảo hình bên), biết $AB = a,AD = b$. Cạnh $DC$ được chia thành $n$ đoạn thẳng bằng nhau bởi các điểm chia ${C_1},{C_2},...,{C_{n - 1}}$, cạnh $AD$ cũng được chia thành $n$ đoạn thẳng bằng nhau bởi các điểm chia ${D_1},{D_2},...,{D_{n - 1}}$. Gọi ${I_k}$ là giao điểm của đoạn $A{C_k}$ với đường thẳng qua ${D_k}$ và song song với $AB$. Biết rằng các điểm ${I_k},(k = 1,2,3,...,n - 1)$ nằm trên một parabol có đỉnh $A$ và trục đối xứng là $AB$. Tính tham số tiêu của parabol nói trên.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}x + \sqrt {x - 2} ,\,\,khi\,\,x \ge 2\\1 - 3x,\,\,\,khi\,\,x < 2\end{array} \right.$. Giá trị $f\left( 1 \right)$ bằng

A. $- 2$.

B. $0$.

C. không xác định.

D. $2$.

Lời giải

Với $x = 1 < 2 \Rightarrow f\left( 1 \right) = 1 - 3.1 =  - 2$.

Đáp án A.

Câu 2: Tập xác định của hàm số $y = \frac{1}{x} + \sqrt {3 - x}$ là

A. $\left( { - \infty ;3} \right]$.

B. $\left[ {3; + \infty } \right)$.

C. $\mathbb{R}\backslash \left\{ 0 \right\}$.

D. $\left( { - \infty ;3} \right]\backslash \left\{ 0 \right\}$.

Lời giải

Điều kiện xác định của hàm số đã cho là

$\left\{ \begin{array}{l}x \ne 0\\3 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \le 3\end{array} \right.$.

Vậy tập xác định của hàm số đã cho là $D = \left( { - \infty ;3} \right]\backslash \left\{ 0 \right\}$.

Đáp án D.

Câu 3: Cho hàm số $y = f\left( x \right) = {x^2}$ xác định trên $\mathbb{R}.$ Xét các mệnh đề sau:

Hàm số $y = f\left( x \right)$ đồng biến trên $\mathbb{R}.$

Hàm số $y = f\left( x \right)$ nghịch biến trên $\left( {0; + \infty } \right).$

Hàm số $y = f\left( x \right)$ đồng biến trên $\left( { - \infty ;0} \right).$

Tìm tất cả các mệnh đề sai trong ba mệnh đề trên.

A. I và II.

B. I và III.

C. II và III.

D. I, II và III.

Lời giải

Hàm số $y = f\left( x \right)$ nghịch biến trên $\left( { - \infty ;0} \right).$

Hàm số $y = f\left( x \right)$ đồng biến trên $\left( {0; + \infty } \right).$

Đáp án D.

Câu 4: Cho hàm số $y = 2{x^2} + 4x - 2023$. Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên khoảng $\left( { - \infty ; - 2} \right)$ và nghịch biến trên khoảng $\left( { - 2; + \infty } \right)$.

B. Hàm số nghịch biến trên khoảng $\left( { - \infty ; - 2} \right)$ và đồng biến trên khoảng $\left( { - 2; + \infty } \right)$.

C. Hàm số đồng biến trên khoảng $\left( { - \infty ; - 1} \right)$ và nghịch biến trên khoảng $\left( { - 1; + \infty } \right)$.

D. Hàm số nghịch biến trên khoảng $\left( { - \infty ; - 1} \right)$ và đồng biến trên khoảng $\left( { - 1; + \infty } \right)$.

Lời giải

Hàm số $y = a{x^2} + bx + c$ với $a > 0$ đồng biến trên khoảng $\left( { - \frac{b}{{2a}}; + \infty } \right)$, nghịch biến trên khoảng $\left( { - \infty ; - \frac{b}{{2a}}} \right)$.

Áp dụng: Ta có $- \frac{b}{{2a}} =  - 1$. Do đó hàm số nghịch biến trên khoảng $\left( { - \infty ; - 1} \right)$ và đồng biến trên khoảng $\left( { - 1; + \infty } \right)$.

Đáp án D.

Câu 5: Hàm số nào có đồ thị như hình vẽ bên dưới?

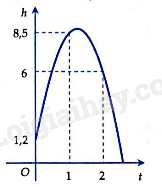
A. $y =  - {x^2} + 4x - 3$.

B. $y =  - {x^2} - 4x - 3$.

C. $y =  - 2{x^2} - x - 3$.

D. $y = {x^2} - 4x - 3$.

Lời giải

Đồ thị có bề lõm quay xuống dưới nên $a < 0$. Loại phương án D.

Trục đối xứng: $x = 2$ do đó chọn A.

Đáp án A.

Câu 6: Tọa độ giao điểm của $\left( P \right)\,:\,y = {x^2} - 4x$ với đường thẳng $d\,:\,y =  - x - 2$ là

A. $M\left( {0;\, - 2} \right)$, $N\left( {2;\, - 4} \right)$.

B. $M\left( { - 1;\, - 1} \right)$, $N\left( { - 2;\,0} \right)$.

C. $M\left( {\, - 3;\,1} \right)$, $N\left( {3;\, - 5} \right)$.

D. $M\left( {1;\, - 3} \right)$, $N\left( {2;\, - 4} \right)$.

Lời giải

Hoành độ giao điểm của $\left( P \right)$ và $d$ là nghiệm của phương trình:

${x^2} - 4x =  - x - 2\, \Leftrightarrow \,{x^2} - 3x + 2 = 0\, \Leftrightarrow \,\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.$.

Vậy tọa độ giao điểm của $\left( P \right)$ và $d$ là $M\left( {1;\, - 3} \right)$, $N\left( {2;\, - 4} \right)$.

Đáp án D.

Câu 7: Trong các biểu thức sau, biểu thức nào là tam thức bậc 2?

A. $f(x) = x + 3$.

B. $f(x) = (m - 1){x^2} + 2x + 5$.

C. $f(x) = 2{x^2} + x - 5$.

D. $f(x) = \frac{{{x^2} + 1}}{{x - 2}}$.

Lời giải

Đáp án C.

Câu 8: Cho tam thức bậc hai $f\left( x \right) = a{x^2} + bx + c\;\;\left( {a \ne 0} \right)$. Khẳng định nào sau đây đúng?

A. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta  < 0\end{array} \right.$.

B. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  > 0\end{array} \right.$.

C. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta  > 0\end{array} \right.$.

D. $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  < 0\end{array} \right.$.

Lời giải

Ta có $f\left( x \right) > 0,\forall x \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  < 0\end{array} \right.$.

Đáp án D.

Câu 9: Bảng xét dấu sau đây là của tam thức bậc 2 nào?

A. $f(x) =  - {x^2} + 5x - 6$.

B. $f(x) = {x^2} + 5x - 6$.

C. $f(x) = {x^2} - 5x - 6$.

D. $f(x) =  - {x^2} - 5x + 6$.

Lời giải

Từ bảng xét dấu ta có $f(x) = 0$ có 2 nghiệm phân biệt $x = 2,\,x = 3$và $f(x) > 0\,khi\,x \in \left( {2;3} \right)$

Do đó $f(x) =  - {x^2} + 5x - 6$.

Đáp án A.

Câu 10: Tập nghiệm của phương trình $\sqrt {{x^2} + 3x - 2}  = \sqrt {1 + x}$ là

A. $\emptyset$

B. $\left\{ { - 3} \right\}$

C. $\left\{ {1; - 3} \right\}$.

D. $\left\{ 1 \right\}$.

Lời giải

$\sqrt {{x^2} + 3x - 2}  = \sqrt {1 + x}$$\Leftrightarrow \left\{ \begin{array}{l}1 + x \ge 0\\{x^2} + 3x - 2 = 1 + x\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}x \ge  - 1\\{x^2} + 2x - 3 = 0\end{array} \right. \Leftrightarrow x = 1$.

Đáp án D.

Câu 11: Phương trình $\sqrt {3{x^2} + 6x + 3}  = 2x + 1$có tập nghiệm là :

A. $\left\{ {1 - \sqrt 3 ;1 + \sqrt 3 } \right\}$.

B. $\left\{ {1 - \sqrt 3 } \right\}$.

C. $\left\{ {1 + \sqrt 3 } \right\}$

D. $\emptyset$.

Lời giải

Ta có : $\sqrt {3{x^2} + 6x + 3}  = 2x + 1 \Leftrightarrow \left\{ \begin{array}{l}2x + 1 \ge 0\\3{x^2} + 6x + 3 = 4{x^2} + 4x + 1\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x \ge  - \frac{1}{2}\\{x^2} - 2x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge  - \frac{1}{2}\\\left[ \begin{array}{l}x = 1 - \sqrt 3 \left( l \right)\\x = 1 + \sqrt 3 \left( n \right)\end{array} \right.\end{array} \right.$.

Đáp án C.

Câu 12: Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $d$ có phương trình $\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - t\end{array} \right.,t \in \mathbb{R}$. Xác định một vectơ pháp tuyến của đường thẳng $d$

A. $\overrightarrow n  = \left( {1;2} \right)$.

B. $\overrightarrow n  = \left( {2; - 1} \right)$.

C. $\overrightarrow n  = \left( { - 2;1} \right)$.

D. $\overrightarrow n  = \left( { - 1;2} \right)$.

Lời giải

Đường thẳng $d$ có phương trình $\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - t\end{array} \right.,\;t \in \mathbb{R}$ nên một vectơ chỉ phương của đường thẳng $d$ là $\overrightarrow u  = \left( {2; - 1} \right)$ do đó một vectơ pháp tuyến là $\overrightarrow n  = \left( {1;2} \right)$.

Đáp án A.

Câu 13: Trong mặt phẳng tọa độ $Oxy$, viết phương trình đường thẳng đi qua điểm $M\left( {2; - 3} \right)$ và có một vectơ pháp tuyến $\overrightarrow n  = \left( {2;1} \right)$

A. $x + y + 1 = 0$.

B. $2x + y - 5 = 0$.

C. $2x - 3y - 1 = 0$.

D. $2x + y - 1 = 0$.

Lời giải

Đường thẳng đi qua điểm $M\left( {2; - 3} \right)$ và có một vectơ pháp tuyến $\overrightarrow n  = \left( {2;1} \right)$có phương trình $2\left( {x - 2} \right) + 1\left( {y + 3} \right) = 0 \Leftrightarrow 2x + y - 1 = 0$.

Đáp án D.

Câu 14: Trong mặt phẳng tọa độ $O\,xy$, cho hai đường thẳng ${d_1}:2x - y\, + \,3 = 0$ và ${d_2}:x + 2y\, + \,1 = 0$. Vị trí tương đối của hai đường thẳng ${d_1}$ và ${d_2}$ là

A. ${d_1}\, \equiv \,{d_2}$.

B. ${d_1}\,{\rm{//}}\,{d_2}$.

C. ${d_1} \bot \,\,{d_2}$.

D. Cắt nhau và không vuông góc.

Lời giải

Ta có: ${d_1}$ và ${d_2}$ lần lượt có véctơ pháp tuyến là $\overrightarrow {{n_1}} \, = \,\left( {2\,;\, - 1} \right),\,\overrightarrow {{n_2}} \, = \,\left( {1\,;\,2} \right)\,$.

Mà $\overrightarrow {{n_1}} \,.\,\overrightarrow {{n_2}} \, = \,2.1\, + \,\left( { - 1} \right).2\, = \,0\,\, \Rightarrow \,\overrightarrow {{n_1}} \, \bot \,\overrightarrow {{n_2}} \,$ $\Rightarrow {d_1}$ và ${d_2}$ vuông góc.

Đáp án C.

Câu 15: Trong mặt phẳng $Oxy,$ góc giữa hai đường thẳng ${\Delta _1}:\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 - 2t\end{array} \right.$ và ${\Delta _2}:\left\{ \begin{array}{l}x =  - 3 + 2t\\y = 1 + 3t\end{array} \right.$ bằng

A. $90^\circ$.

B. $45^\circ$.

C. $60^\circ$.

D. $30^\circ$.

Lời giải

Hai đường thẳng ${\Delta _1},{\Delta _2}$ lần lượt có vectơ chỉ phương $\overrightarrow {{u_1}}  = \left( {3; - 2} \right)$ và $\overrightarrow {{u_2}}  = \left( {2;3} \right)$.

Vì $\overrightarrow {{u_1}} .\overrightarrow {{u_2}}  = 0$ nên ${\Delta _1} \bot {\Delta _2}$. Suy ra $\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ .$

Đáp án A.

Câu 16: Trong mặt phẳng $Oxy$, cho điểm $M\left( { - 2\,\,;\,\,1} \right)$ và đường thẳng $\Delta :\,\,x - 3y + 6 = 0$. Khoảng cách từ điểm $M$ đến đường thẳng $\Delta$ bằng

A. $\frac{{\sqrt {10} }}{{10}}.$

B. $2\sqrt {10} .$

C. $\frac{{\sqrt {10} }}{5}.$

D. $\frac{2}{{\sqrt {10} }}.$

Lời giải

Công thức tính khoảng cách từ điểm $M\left( {{x_{\rm{o}}}\,;\,\,{y_{\rm{o}}}} \right)$ đến đường thẳng $\Delta :\,\,Ax + By + C = 0$ là

$d\left( {M,\,\Delta } \right) = \frac{{\left| {A{x_{\rm{o}}} + B{y_{\rm{o}}} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$.

Vậy khoảng cách từ điểm $M\left( { - 2\,;\,\,1} \right)$ đến đường thẳng $\Delta :\,\,x - 3y + 6 = 0$ bằng

$d\left( {M,\Delta } \right) = \frac{{\left| { - 2 - 3.1 + 6} \right|}}{{\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt {10} }}{{10}}$.

Đáp án A.

Câu 17: Phương trình nào sau đây không phải là phương trình đường tròn?

A. ${x^2} + {y^2} - 100y + 1 = 0$.

B. ${x^2} + {y^2} - y = 0$.

C. ${x^2} + {y^2} - 2 = 0$.

D. ${x^2} + {y^2} - x + y + 4 = 0$.

Lời giải

Xét đáp án A ta có ${a^2} + {b^2} - c = {0^2} + {50^2} - 1 = 2499 > 0$ là phương trình đường tròn.

Xét đáp án B ta có ${a^2} + {b^2} - c = {0^2} + {\left( {\frac{1}{2}} \right)^2} - 0 = \frac{1}{4} > 0$ là phương trình đường tròn.

Xét đáp án C ta có ${a^2} + {b^2} - c = {0^2} + {0^2} + 2 = 2 > 0$ là phương trình đường tròn.

Xét đáp án D ta có ${a^2} + {b^2} - c = {\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{{ - 1}}{2}} \right)^2} - 4 =  - \frac{7}{2} < 0$ không là phương trình đường tròn.

Đáp án D.

Câu 18: Viết phương trình đường tròn có tâm $A\left( {2\;;\; - 5} \right)$ và tiếp xúc với đường thẳng

$d:3x - 4y - 1 = 0$.

A. ${\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 25$.

B. ${\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 25$.

C. ${\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 5$.

D. ${\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 5$.

Lời giải

Đường tròn có tâm $A\left( {2\;;\; - 5} \right)$ và tiếp xúc với đường thẳng $d:3x - 4y - 1 = 0$

$\Rightarrow R = d\left( {A\;,\;d} \right) = \frac{{\left| {3.2 - 4.\left( { - 5} \right) - 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{25}}{5} = 5$.

Vậy phương trình đường tròn cần tìm là: ${\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 25$.

Đáp án A.

Câu 19: Tọa độ các đỉnh của hypebol $\left( H \right):\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} = 1$ là

A. ${A_1} = \left( { - 5;0} \right);{A_2} = \left( {5;0} \right)$.

B. ${A_1} = \left( {0; - 4} \right);{A_2} = \left( {0;4} \right)$.

C. ${A_1} = \left( { - 4;0} \right);{A_2} = \left( {4;0} \right)$.

D. ${A_1} = \left( {0; - 5} \right);{A_2} = \left( {0;5} \right)$.

Lời giải

Từ phương trình $\left( H \right):\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} = 1$, ta có: ${a^2} = 25 \Rightarrow a = 5,\left( {a > 0} \right)$.

Gọi ${A_1}$ và ${A_2}$ là hai đỉnh của $\left( H \right)$.

Vậy tọa độ các đỉnh của $\left( H \right)$là ${A_1} = \left( { - 5;0} \right);{A_2} = \left( {5;0} \right)$.

Đáp án A.

Câu 20: Cho Parapol$\left( P \right):{y^2} = 2px\,\left( {p > 0} \right)$. Chọn mệnh đề đúng trong các mệnh đề sau:

A. $\left( P \right)$ có tiêu điểm $F\left( {0\,;\,\frac{p}{2}} \right).$

B. $\left( P \right)$ có tiêu điểm $F\left( { - \frac{p}{2}\,;\,0} \right).$

C. $\left( P \right)$ có phương trình đường chuẩn $\Delta :y = \frac{p}{2}.$

D. $\left( P \right)$ có phương trình đường chuẩn $\Delta :x =  - \frac{p}{2}.$

Lời giải

Theo tính chất của Parabol $\left( P \right):{y^2} = 2px\,\left( {p > 0} \right).$

Ta có $\left( P \right)$ có tiêu điểm $F\left( {\frac{p}{2}\,;\,0} \right)$và có phương trình đường chuẩn $\Delta :x =  - \frac{p}{2}.$

Do đó mệnh đề đúng là đáp án D.

Đáp án D.

Câu 21: Tìm tập xác định ${\rm{D}}$ của hàm số $y = \frac{{x + 1}}{{\left( {x - 3} \right)\sqrt {2x - 1} }}$.

A. ${\rm{D}} = \left( { - \frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}$.

B. ${\rm{D}} = \left[ {\frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}$.

C. ${\rm{D}} = \left( {\frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}$.

D. ${\rm{D}} = \mathbb{R}$.

Lời giải

Hàm số xác định khi $\left\{ \begin{array}{l}x - 3 \ne 0\\2x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 3\\x > \frac{1}{2}\end{array} \right..$

Vậy tập xác định của hàm số là ${\rm{D}} = \left( {\frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}$.

Đáp án C.

Câu 22: Có bao nhiêu số nguyên $m \in \left[ { - 2022;\,2022} \right]$để hàm số $y = \sqrt {m - 2x}$ xác định trên khoảng $\left( { - 3; - 1} \right)$?

A. $2022$.

B. $2025$.

C. $2021$.

D. $4042$.

Lời giải

Hàm số xác định khi và chỉ khi $m - 2x \ge 0 \Leftrightarrow x \le \frac{m}{2}$.

TXĐ của hàm số là $D = \left( { - \infty ;\,\frac{m}{2}} \right]$.

Hàm số xác định trên khoảng $\left( { - 3;\, - 1} \right)$ khi $\left( { - 3;\, - 1} \right) \subset \left( { - \infty ;\,\frac{m}{2}} \right] \Leftrightarrow  - 1 \le \frac{m}{2} \Leftrightarrow m \ge  - 2$.

Với $m \in \left[ { - 2022;\,2022} \right]$, $m \in \mathbb{Z}$, suy ra $m \in \left\{ { - 2; - 1;...;2022} \right\}$. Vậy có $2025$ số thỏa mãn.

Đáp án B.

Câu 23: Tìm tất cả các giá trị của tham số $m$để hàm số $y = f\left( x \right) = \left( {m - 4} \right)x + {m^2} - m - 2$ đồng biến trên tập xác định của nó.

A. $m > 4$.

B. $m \ge 4$.

C. $m < 4$.

D. $m \le 4$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Hàm số đã cho đồng biến trên $\mathbb{R} \Leftrightarrow$ $m - 4 > 0 \Leftrightarrow m > 4$

Đáp án B.

Câu 24: Biết rằng $\left( P \right):y = a{x^2} - 4x + c$ có hoành độ đỉnh bằng $- 3$ và đi qua điểm $M\left( { - 2;1} \right)$. Tính tổng $S = a + c$

A. $S = 5$.

B. $S =  - 5$.

C. $S = 4$.

D. $S = 1$.

Lời giải

Vì $\left( P \right)$ có hoành độ đỉnh bằng $- 3$ và đi qua điểm $M\left( { - 2;1} \right)$ nên ta có hệ

$\left\{ \begin{array}{l} - \frac{{ - 4}}{{2a}} =  - 3\\4a + 8 + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4 = 6a\\4a + c =  - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \frac{2}{3}\\c =  - \frac{{13}}{3}\end{array} \right. \Rightarrow S = a + c =  - 5$

Đáp án B.

Câu 25: Xác định $\left( P \right):y = a{x^2} - 6x + c$, biết $\left( P \right)$ có trục đối xứng $x =  - 4$ và cắt $Ox$ tại hai điểm có độ dài bằng $4$.

A. $\left( P \right):y =  - \frac{3}{4}{x^2} - 6x - 9$.

B. $\left( P \right):y = \frac{3}{4}{x^2} - 6x - 9$.

C. $\left( P \right):y =  - \frac{3}{4}{x^2} - 6x + 9$.

D. $\left( P \right):y = \frac{3}{4}{x^2} - 6x + 9$.

Lời giải

Vì $\left( P \right):y = a{x^2} - 6x + c$, biết $\left( P \right)$ có trục đối xứng $x =  - 4$ nên

$\frac{6}{{2a}} =  - 4 \Leftrightarrow a =  - \frac{3}{4}$ $\Rightarrow \left( P \right):y =  - \frac{3}{4}{x^2} - 6x + c$.

Phương trình hoành độ giao điểm của $\left( P \right)$ và $Ox$ là: $- \frac{3}{4}{x^2} - 6x + c = 0\,\,\,\,\left( * \right)$.

$\left( * \right)$ có hai nghiệm phân biệt $\Leftrightarrow \Delta ' = 9 + \frac{3}{4}c > 0 \Leftrightarrow c >  - 12$.

Khi đó $\left( * \right)$ có hai nghiệm ${x_1},\,\,{x_2}$ thỏa mãn $\left\{ \begin{array}{l}{x_1} + {x_2} =  - 8\\{x_1}.{x_2} =  - \frac{{4c}}{3}\end{array} \right.$.

Mà $\left| {{x_2} - {x_1}} \right| = 4$

$\Leftrightarrow {\left( {{x_2} - {x_1}} \right)^2} = 16 \Leftrightarrow {\left( {{x_2} + {x_1}} \right)^2} - 4{x_1}{x_2} = 16$

$\Leftrightarrow {( - 8)^2} + \frac{{16c}}{3} = 16\, \Leftrightarrow c =  - 9$ (t/m).

Vậy $\left( P \right):y =  - \frac{3}{4}{x^2} - 6x - 9$.

Đáp án A.

Câu 26: Tìm tập xác định của hàm số $y = \sqrt {2{x^2} - 5x + 2}$.

A. $\left( { - \infty ;\frac{1}{2}} \right]$.

B. $\left[ {2; + \infty } \right)$.

C. $\left( { - \infty ;\frac{1}{2}} \right] \cup \left[ {2; + \infty } \right)$.

D. $\left[ {\frac{1}{2};2} \right]$.

Lời giải

Điều kiện $2{x^2} - 5x + 2 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le \frac{1}{2}\end{array} \right.$. Vậy tập xác định của hàm số là $\left( { - \infty ;\frac{1}{2}} \right] \cup \left[ {2; + \infty } \right)$.

Đáp án C.

Câu 27: Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $\left( {2{m^2} + m - 6} \right){x^2} + \left( {2m - 3} \right)x - 1 > 0$?

A. $- \frac{5}{6} < m \le \frac{3}{2}$.

B. $- \frac{5}{6} < m < \frac{3}{2}$.

C. $- \frac{5}{6} \le m < \frac{3}{2}$.

D. $- \frac{5}{6} \le m \le \frac{3}{2}$.

Lời giải

Bất phương trình $\left( {2{m^2} + m - 6} \right){x^2} + \left( {2m - 3} \right)x - 1 > 0{\rm{   }}\left( * \right)$ vô nghiệm khi và chỉ khi $\left( {2{m^2} + m - 6} \right){x^2} + \left( {2m - 3} \right)x - 1 \le 0,\forall x \in \mathbb{R}$

* Xét $2{m^2} + m - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}m =  - 2\\m = \frac{3}{2}\end{array} \right.$

Với $m =  - 2$ thì bpt $\left( * \right)$ $\Leftrightarrow  - 7x - 1 > 0 \Leftrightarrow x <  - \frac{1}{7}$, loại $m =  - 2$.

Với $m = \frac{3}{2}$ thì bpt $\left( * \right)$ $\Leftrightarrow 0x - 1 > 0$ bpt vô nghiệm, nhận $m = \frac{3}{2}$.

* Xét $2{m^2} + m - 6 \ne 0$

$\left( {2{m^2} + m - 6} \right){x^2} + \left( {2m - 3} \right)x - 1 \le 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}2{m^2} + m - 6 < 0\\{\left( {2m - 3} \right)^2} - 4.\left( {2{m^2} + m - 6} \right).\left( { - 1} \right) \le 0\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} - 2 < m < \frac{3}{2}\\ - \frac{5}{6} \le m \le \frac{3}{2}\end{array} \right.$

$\Leftrightarrow  - \frac{5}{6} \le m < \frac{3}{2}$

Vậy $- \frac{5}{6} \le m \le \frac{3}{2}$ thì bất phương trình $\left( * \right)$ vô nghiệm.

Đáp án D.

Câu 28: Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \sqrt {\left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1}$ có tập xác định là $\mathbb{R}$?

A. $m > \frac{7}{3}$.

B. $m < \frac{7}{3}$.

C. $m \le \frac{7}{3}$.

D. $m \ge \frac{7}{3}$.

Lời giải

Hàm số có tập xác định là $\mathbb{R}$ khi và chỉ khi $f\left( x \right) = \left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1 \ge 0,\forall x \in \mathbb{R}$

* Xét $m - 2 = 0 \Leftrightarrow m = 2$ thì $f\left( x \right) = 2x + 1 \ge 0 \Leftrightarrow x \ge  - \frac{1}{2}$, loại $m = 2$.

* Xét $m \ne 2$

$\left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1 \ge 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}m - 2 > 0\\{\left( {m - 3} \right)^2} - \left( {m - 2} \right)\left( {m - 1} \right) \le 0\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}m > 2\\m \ge \frac{7}{3}\end{array} \right. \Leftrightarrow m \ge \frac{7}{3}$

Vậy $m \ge \frac{7}{3}$

Đáp án D.

Câu 29: Phương trình $\sqrt {{x^2} + 2x - 3}  = 5 - x$ có nghiệm là $x = \frac{a}{b}$. Khi đó $a + 2b$bằng:

A. $10$.

B. $33$.

C. $17$.

D. $13$.

Lời giải

Ta có: $\sqrt {{x^2} + 2x - 3}  = 5 - x$

$\Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x - 3 \ge 0\\5 - x \ge 0\\{x^2} + 2x - 3 = {\left( {5 - x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \le  - 3\\x \ge 1\end{array} \right.\\x \le 5\\12x = 28\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \le  - 3\\x \ge 1\end{array} \right.\\x \le 5\\x = \frac{7}{3}\end{array} \right. \Leftrightarrow x = \frac{7}{3}$.

Vậy $a = 7;b = 3$. Suy ra $a + 2b = 13$.

Đáp án D.

Câu 30: Phương trình tổng quát của đường thẳng $d$ đi qua $A\left( {1; - 2} \right)$ và vuông góc với đường thẳng $\Delta :3x - 2y + 1 = 0$ là:

A. $3x - 2y - 7 = 0.$

B. $2x + 3y + 4 = 0.$

C. $x + 3y + 5 = 0.$

D. $2x + 3y - 3 = 0.$

Lời giải

Ta có $d \bot \Delta$ nên $d$ có một vectơ pháp tuyến là $\overrightarrow n  = \left( {2;3} \right).$

Mà đường thẳng $d$ đi qua $A\left( {1; - 2} \right)$ nên phương trình tổng quát của đường thẳng $d$ là:

$2\left( {x - 1} \right) + 3\left( {y + 2} \right) = 0 \Leftrightarrow 2x + 3y + 4 = 0.$

Vậy phương trình tổng quát của đường thẳng $d:2x + 3y + 4 = 0.$

Đáp án B.

Câu 31: Trong mặt phẳng $Oxy,$ gọi S là tập hợp tất cả các giá trị của tham số m để góc giữa hai đường thẳng $d:mx + \left( {m - 1} \right)y + 2 = 0$ và $\Delta :x - y + 2 = 0$ bằng $30^\circ .$ Tích tất cả các phần tử của tập S bằng

A. $1$.

B. $- \frac{1}{6}$.

C. $\frac{1}{6}$.

D. $- 1$.

Lời giải

Đường thẳng $d$ nhận $\overrightarrow {{n_1}}  = \left( {m;m - 1} \right)$ là 1 véctơ pháp tuyến.

Đường thẳng $\Delta$ nhận $\overrightarrow {{n_2}}  = \left( {1; - 1} \right)$ là 1 véctơ pháp tuyến.

Ta có: $\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} \Leftrightarrow \frac{{\sqrt 3 }}{2} = \frac{{\left| {m - 1.\left( {m - 1} \right)} \right|}}{{\sqrt {{m^2} + {{\left( {m - 1} \right)}^2}} \sqrt 2 }}$.

$\Leftrightarrow \frac{{\sqrt 3 }}{2} = \frac{1}{{\sqrt 2 \sqrt {2{m^2} - 2m + 1} }} \Leftrightarrow \sqrt {3\left( {2{m^2} - 2m + 1} \right)}  = \sqrt 2  \Leftrightarrow 6{m^2} - 6m + 1 = 0.$

Vì $\Delta ' = 3 > 0 \Rightarrow$ phương trình có 2 nghiệm phân biệt và ${m_1}.{m_2} = \frac{1}{6}$.

Đáp án C.

Câu 32: Tâm đường tròn ${x^2} + {y^2} - 10x + 1 = 0$ cách trục $Oy$ một khoảng bằng

A. $5$.

B. $0$.

C. $10$.

D. $- 5$.

Lời giải

Đường tròn ${x^2} + {y^2} - 10x + 1 = 0$ có tâm $I\left( {5;0} \right)$.

Khoảng cách từ $I$ đến $Oy$ là $d\left( {I,Oy} \right) = 5$.

Đáp án A.

Câu 33: Tìm tất cả giá trị của tham số $m$ để phương trình ${x^2} + {y^2} + 2mx - 10y + 4m = 0$ là

phương trình đường tròn và có bán kính nhỏ nhất.

A. $m = \frac{1}{2}$.

B. $m = 1$.

C. $m =  - 2$.

D. $m = 2$.

Lời giải

Phương trình ${x^2} + {y^2} + 2mx - 10y + 4m = 0$ là phương trình đường tròn

$\Leftrightarrow {a^2} + {b^2} - c > 0$$\Leftrightarrow {\left( { - m} \right)^2} + {5^2} - 4m > 0$$\Leftrightarrow {m^2} - 4m + 25 > 0$$\Leftrightarrow m \in \mathbb{R}$.

Bán kính $R = \sqrt {{a^2} + {b^2} - c}  = \sqrt {{m^2} - 4m + 25}  = \sqrt {{m^2} - 4m + 4 + 21}  = \sqrt {{{\left( {m - 2} \right)}^2} + 21}  \ge \sqrt {21}$.

Bán kính nhỏ nhất là $R = \sqrt {21}$ khi $m - 2 = 0 \Leftrightarrow m = 2$.

Đáp án D.

Câu 34: Tổng các khoảng cách từ một điểm bất kỳ nằm trên elip $\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$ tới hai tiêu điểm bằng

A. $4.$

B. $6.$

C. $12.$

D. $\sqrt 5 .$

Lời giải

Ta có $\left\{ \begin{array}{l}{a^2} = 9\\{b^2} = 4\end{array} \right.$$\Rightarrow a = 3$.

Tổng các khoảng cách từ một điểm bất kỳ nằm trên elip tới hai tiêu điểm bằng $2a = 2.3 = 6$.

Đáp án B.

Câu 35: Cho của hypebol $\left( H \right):\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{5} = 1$. Hiệu các khoảng cách từ mỗi điểm nằm trên $\left( H \right)$ đến hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?

A. $8$.

B. $16$.

C. $4$.

D. $5$.

Lời giải

Gọi ${F_1}$ và ${F_2}$ là hai tiêu điểm của $\left( H \right):\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1,\left( {a > 0,b > 0} \right)$.

Điểm $M \in \left( H \right) \Leftrightarrow \left| {M{F_1} - M{F_2}} \right| = 2a$.

Từ phương trình $\left( H \right):\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{5} = 1$ suy ra ${a^2} = 16 \Rightarrow a = 4,\left( {a > 0} \right)$.

Vậy hiệu các khoảng cách từ mỗi điểm $M$nằm trên $\left( H \right)$đến hai tiêu điểm có giá trị tuyệt đối là $\left| {M{F_1} - M{F_2}} \right| = 2a = 8$.

Đáp án A.

Phần tự luận (3 điểm)

Bài 1. Một công ty bắt đầu sản xuất và bán một loại xe máy từ năm 2018. Số lượng loại xe máy đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 4 nghìn và $4,5$ nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm kể từ 2018, số lượng xe máy loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm số bậc hai. Giả sử $t$ là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại xe máy đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diễn bởi các điểm $\left( {0;\,4} \right)$ và $\left( {1;\,4,5} \right)$. Giả sử điểm $\left( {0;\,4} \right)$ là đỉnh đồ thị của hàm số bậc hai này. Hỏi đến năm bao nhiêu thì số lượng xe máy đó bán được trong năm sẽ vượt mức 40 nghìn chiếc?

Lời giải

Vì số lượng xe máy loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm số bậc hai nên gọi hàm số này có dạng $y = a{t^2} + bt + c$ (trong đó $t$ là thời gian (đơn vị năm), $y$ là số lượng xe máy bán được qua từng năm (đơn vị nghìn chiếc)).

Điểm $\left( {0;\,4} \right)$ là đỉnh đồ thị của hàm số bậc hai, ta có $\left\{ \begin{array}{l} - \frac{b}{{2a}} = 0\\c = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 0\\c = 4\end{array} \right.$.

Đồ thị hàm số đi qua điểm $\left( {1;\,4,5} \right)$, ta có $a + 4 = 4,5 \Leftrightarrow a = 0,5$.

Hàm số cần tìm là $y = 0,5{t^2} + 4$.

Để số lượng xe máy đó bán được vượt mức 40 nghìn chiếc thì

$0,5{t^2} + 4 > 40$$\Leftrightarrow {t^2} > 72$$\Rightarrow t > \sqrt {72}  \approx 8,5$$\Rightarrow t \approx 9$ (năm).

Vậy đến năm 2027 thì số lượng xe máy đó bán được vượt mức 40 nghìn chiếc.

Bài 2. Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $d$ đi qua điểm $M\left( {1;2} \right)$ và cắt tia $Ox$, tia $Oy$ lần lượt tại $A,B$ sao cho tam giác $OAB$ có diện tích nhỏ nhất. Hãy viết phương trình của $d.$

Lời giải

Do $A,B$ lần lượt thuộc tia $Ox,Oy$ và tồn tại tam giác $OAB$ nên ta có $A\left( {a;0} \right),B\left( {0;b} \right)$ với $a > 0$, $b > 0$. Lúc này, ta có:

+ Phương trình đường thẳng $d$ là $\frac{x}{a} + \frac{y}{b} = 1$.

$M\left( {1;2} \right) \in d$$\Rightarrow$$\frac{1}{a} + \frac{2}{b} = 1$.

+ Diện tích tam giác $OAB$: ${S_{OAB = }}\frac{1}{2}OA.OB = \frac{1}{2}ab$ (do $OA = |a| = a,OB = |b| = b$).

+ Áp dụng bất đẳng thức AM-GM, ta có:

$\frac{1}{a} + \frac{2}{b} \ge 2\sqrt {\frac{1}{a}.\frac{2}{b}}$$\Rightarrow$$\frac{1}{2}ab \ge 4$$\Rightarrow$${S_{OAB}} \ge 4$.

Dấu  xảy ra $\Leftrightarrow$$\left\{ \begin{array}{l}\frac{1}{a} + \frac{2}{b} = 1\\\frac{1}{a} = \frac{2}{b}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\end{array} \right.$.

Vậy phương trình đường thẳng $d$ là $\frac{x}{2} + \frac{y}{4} = 1 \Leftrightarrow 2x + y - 4 = 0$.

Bài 3. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ $Oth,$ trong đó $t$ là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; $h$ là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao $1,2m$. Sau đó $1$ giây, nó đạt độ cao $8,5m$và $2$ giây sau khi đá lên, nó đạt độ cao $6m$. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm)?

Lời giải

Gọi phương trình của parabol quỹ đạo là $h = a{t^2} + bt + c$.

Từ giả thiết suy ra parabol đi qua các điểm $\left( {0;1;2} \right)$, $\left( {1;8;5} \right)$ và $\left( {2;6} \right)$.

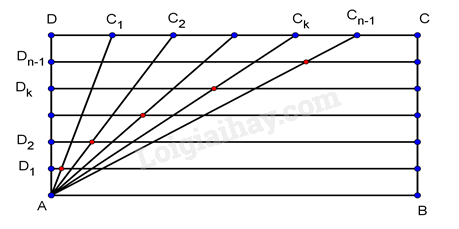
Từ đó ta có

$\left\{ \begin{array}{l}c = 1,2\\a + b + c = 8,5\\4a + 2b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 4,9\\b = 12,2\\c = 1,2\end{array} \right.$.

Vậy phương trình của parabol quỹ đạo là $h =  - 4,9{t^2} + 12,2t + 1,2$.

Giải phương trình

$h = 0 \Leftrightarrow  - 4,9{t^2} + 12,2t + 1,2 = 0$ ta tìm được một nghiệm dương là $t \approx 2,58$.

Bài 4. Cho hình chữ nhật $ABCD$ ( tham khảo hình bên), biết $AB = a,AD = b$. Cạnh $DC$ được chia thành $n$ đoạn thẳng bằng nhau bởi các điểm chia ${C_1},{C_2},...,{C_{n - 1}}$, cạnh $AD$ cũng được chia thành $n$ đoạn thẳng bằng nhau bởi các điểm chia ${D_1},{D_2},...,{D_{n - 1}}$. Gọi ${I_k}$ là giao điểm của đoạn $A{C_k}$ với đường thẳng qua ${D_k}$ và song song với $AB$. Biết rằng các điểm ${I_k},(k = 1,2,3,...,n - 1)$ nằm trên một parabol có đỉnh $A$ và trục đối xứng là $AB$. Tính tham số tiêu của parabol nói trên.

Lời giải

Chọn hệ trục tọa độ $Oxy$ sao cho $O$ trùng với điểm $A$, $AB$ nằm trên tia $Ox$ và $AD$ nằm trên tia $Oy$.

Khi đó ta có phương trình đường thẳng qua ${D_k}$ và song song với $AB$ là $y = k.\frac{b}{n}$.

Tọa độ điểm ${C_k}\left( {k.\frac{a}{n};b} \right)$, suy ra phương trình đường $A{C_k}$ là $y = \frac{{bn}}{{ak}}x$.

Tọa độ điểm ${I_k}$ là nghiệm của hệ phương trình $\left\{ \begin{array}{l}y = k.\frac{b}{n}\\y = \frac{{bn}}{{ak}}x\end{array} \right.$.

Giải hệ phương trình ta được $\left\{ \begin{array}{l}x = a.\frac{{{k^2}}}{{{n^2}}}\\y = k.\frac{b}{n}\end{array} \right. \Rightarrow {I_k}\left( {a.\frac{{{k^2}}}{{{n^2}}};k.\frac{b}{n}} \right)$.

Giả sử ${I_k}\left( {{x_k};{y_k}} \right) \Rightarrow y_k^2 = \frac{{{b^2}}}{a}{x_k}.$ Suy ra điểm ${I_k}$ thuộc parabol có phương trình ${y^2} = \frac{{{b^2}}}{a}x$. Khi đó tham số tiêu của parabol nói trên bằng $\frac{{{b^2}}}{{2a}}$.